б) При помощи тригонометрической окружности отберём корни, принадлежащие заданному отрезку.
Получим
Ответ: a) 
б) 
14. В правильной треугольной призме АВСА′B′C′ сторона основания АВ равна 6, а боковое ребро АА′ равно 3. На ребре АВ отмечена точка К так, что АК = 1. Точки М и L — середины рёбер А′С′ и В′С′ соответственно. Плоскость γ параллельна прямой АС и содержит точки К и L.
а) Докажите, что прямая ВМ перпендикулярна плоскости γ;
б) Найдите расстояние от точки С до плоскости γ.
Решение.
Построим сечение призмы плоскостью γ. а) Проведём КР || АС, 
, CP = 1. Проведём PL, проведём LR || AC, 
Проведём RK. Трапеция LPLR — искомое сечение. Сечение параллельно АС по признаку параллельности прямой к плоскости.
Введём систему координат, как показано на рисунке. В этой системе координат: В (0; 0; 0), С (0; 6; 0), В' (0; 0; 3), C' (0; 6; 3), 
P (0; 5; 0), 
Тогда
Откуда получаем:
Так как 
и 
получаем, что 
Что и требовалось доказать.
б) Далее заметим, что плоскость сечения перпендикулярна вектору 
, найдем уравнение плоскости и вычислим расстояние от точки до плоскости:
Найдём свободный член D в уравнении плоскости 
подставив координаты точки К:
поэтому 
Упростив уравнение плоскости, получим: 
Тогда для искомого расстояния получаем:
Приведем другое решение.
а) Четырёхугольник RLPK — искомое сечение. Проведём плоскость B'MTB. Имеем:
Рассмотрим прямоугольник BB'MT. Заметим, что LR — средняя линия треугольника A'B'C', тогда F' — середина B'M, тогда
(Δ BKF ~ Δ BAT):
Пусть теперь 
Тогда 
На продолжении TB за точку B отметим точку F'', такую, что 
. Тогда 
и 
Далее,
По обратной теореме Пифагора, треугольник FF'F'' прямоугольный 
следовательно, 
Это и требовалось доказать.
б) Заметим, что так как 
то 
Пусть основанием перпендикуляра опущенного из T на γ будет являться точка S. Тогда TS || BM || F''F. Таким образом, треугольники FTS и FF''F' будут подобны. Следовательно, 
откуда 
Ответ: б) 
Еще один подход к решению задачи, не использующий метод координат, укажем на примере задачи 514653.
15. Решите неравенство 
Решение.
Пусть 
Получаем систему неравенств:
Следовательно:
Таким образом, решением исходного неравенства является множество 
Ответ: 
16. Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17.
а) Докажите, что диагонали перпендикулярны.
б) Найдите площадь трапеции.
Решение.
а) Проведем через точку 
прямую параллельную 
. На пересечении этой прямой и прямой 
отметим точку 
, 
— параллелограмм.
В треугольнике ACC 1: 
Заметим, что 
поскольку 
, тогда по теореме, обратной теореме Пифагора, треугольник ACC 1 — прямоугольный, угол ACC 1 прямой. Тогда угол COD прямой, что и требовалось доказать.
б) 
Ответ: б) 60.
17. Банк планирует вложить на 1 год 30% имеющихся у него средств клиентов в акции золотодобывающего комбината, а остальные 70% — в строительство торгового комплекса. В зависимости от обстоятельств первый проект может принести банку прибыль в размере от 32% до 37% годовых, а второй проект — от 22 до 27% годовых. В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке, уровень которой должен находиться в пределах от 10% до 20% годовых. Определите, какую наименьшую и наибольшую чистую прибыль в процентах годовых от суммарных вложений в покупку акций и строительство торгового комплекса может при этом получить банк.
Решение.
Пусть средства клиентов, имеющихся в банке, составляет S у.е.
Наименьшая прибыль, которую банку могут принести оба проекта 0,25 S.
Банк получит наименьшую чистую прибыль если он своим клиентам выплатит проценты по высшей ставке (20%). Рассчитаем этот показатель: 
Наибольшая прибыль, которую банку могут принести оба проекта 0,3 S.
Банк получит наибольшую чистую прибыль, если банк своим клиентам выплатит проценты по низшей ставке (10%).
Ответ: 5%; 20%.
18. Найдите все значения 
при каждом из которых система
имеет единственное решение.
Решение.
Решение системы может быть единственным в двух случаях.
1 случай. Единственное решение является граничной точкой для множества решений каждого из двух неравенств. В этом случае это единственное решение должно удовлетворять системе уравнений
Вычитая из второго уравнения первое, получаем:
Если 
то 
а значит, 
При этом значении 
система принимает вид:
Единственное решение 
Если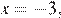 
то 
и 
Система принимает вид:
При этом значении 
система имеет бесконечно много решений.
2 случай. Одно из неравенств имеет единственное решение, удовлетворяющее другому неравенству.
Первое неравенство имеет единственное решение при
При этом первое неравенство имеет единственное решение 
которое удовлетворяет второму неравенству.
Второе неравенство имеет единственное решение при
При этом второе неравенство имеет единственное решение 
которое не удовлетворяет первому неравенству.
Ответ: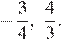 
______________________
дублирует задание 508976
19. Пусть q — наименьшее общее кратное, а d — наибольший общий делитель натуральных чисел x и y, удовлетворяющих равенству 3 x = 8 y − 29.
а) Может ли 
быть равным 170?
б) Может ли 
быть равным 2?
в) Найдите наименьшее значение 
Решение.
а) Для чисел x = 17 и y = 10 выполняется условие 3 x = 8 y −29, q = 170, d = 1, 
б) и в) При x = 1 и y = 4 выполняется равенство 3 x = 8 y − 29 и 
Покажем, что никакое значение 
не реализуется.
Если x = y, то 
что невозможно, поскольку числа x и y — натуральные. Пусть для определённости x < y и x = ad, a y = bd. Тогда натуральные числа a и b взаимно просты и a < b. Получаем 
откуда 
Если 
то a = b, что невозможно.
Если 
то a = 1, b = 2 и, значит, y = 2 x, откуда 
что невозможно.
Если 
то a = 1, b = 3 и, значит, y = 3 x, откуда 
что невозможно.
Ответ: а) да; б) нет) в) 4.