Элементы векторной алгебры.

Томский государственный университет систем управления и радиоэлектроники

Приходовский М.А.

Математика

Курс практических занятий

Семестр 1

Учебное пособие

Для специальностей

Информатика и вычислительная техника»

Инфокоммуникационные технологии и системы связи»

Радиоэлектронные системы и комплексы»

Томск

ТУСУР

 

 

Электронное учебное пособие составлено по материалам практических занятий в группах 589-1,2,3, 129, 1В9 осенью 2019 года.

 

Пособие может представлять методический интерес для преподавателей, работающих на аналогичных специальностях, как материал для планирования занятий.

 

 

Оглавление по темам

Действия над матрицами............................................................... Определители................................................................................. Обратная матрица........................................................................... Ранг матрицы................................................................................... Элементы векторной алгебры.......……………………….……… Системы линейных уравнений…………....................................... Системы линейных однородных уравнений................................. Линейные операторы....................................................................... Прямая на плоскости....................................................................... Плоскость в пространстве.............................................................. Прямая в пространстве................................................................... Полярная система координат......................................................... Множества и функции.................................................................... Пределы.......................................................................................... 1-й замечательный предел.............................................................. 2-й замечательный предел.............................................................. Главная часть бесконечно-малой................................................... Непрерывность и точки разрыва.................................................... Дифференциальное исчисление...................................................... Частные производные и градиент.................................................. Уравнение касательной.................................................................. Экстремумы, наибольшее и наименьшее значение...................... Выпуклость графика и 2 производная........................................... Асимптоты........................................................................................

 

 

Таблица соответствия дат занятий и номеров задач.

1В9		589-3
04.09.2019 1-15	06.09.2019 1-17	05.09.2019 1-17
06.09.2019 16-31	10.09.2019 18-31	10.09.2019 18-31
11.09.2019 32-40	13.09.2019 32-41	12.09.2019 32-40
12.09.2019 41-44	16.09.2019 42-48	16.09.2019 41-52
18.09.2019 45-57	20.09.2019 49-63	19.09.2019 53-63
20.09.2019 58-71

 

 

Действия над матрицами.

Задача 1. Найти сумму и разность матриц: +

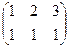
Решение. Складываем поэлементно:

= .

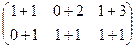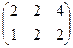Вычитаем:

= .

Ответ. Сумма: 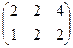разность: .

Задача 2. Найти сумму матриц: +

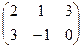
Решение. Складываем поэлементно:

= .

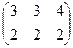Ответ. .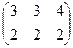

Задача 3. Даны матрицы , .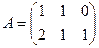

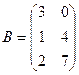Найти 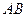и .

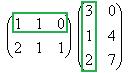
Решение. Запишем эти матрицы. Если первую разбить на строки, а вторую на столбцы, то видно, что есть всего 4 варианта скалярно умножить друг на друга вектор-строку их первой на вектор-столбец из второй.

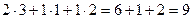
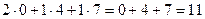
Например, если умножаем строку номер 1 на столбец номер 2, то и число, которое при этом получается, ставим в 1 строку 2 столбец новой матрицы. Итак,

= .

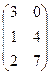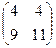Теперь найдём . В данном случае первую матрицу можно разрезать на 3 строки, а вторую на 3 столбца. Таким образом, получаем 9 чисел.

Покажем, например, как 1-я строка скалярно умножается на 1-й столбец, они обведены. .

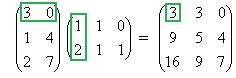
Ответ. .

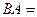
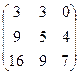Задача 4. Найти произведения матриц:

, , .

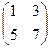
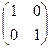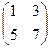
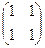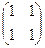
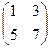Решение.

= = = .

= = = .

= = = .

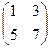
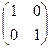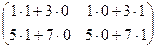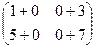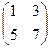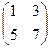
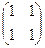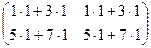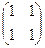
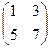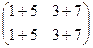Ответ. , , .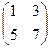

Примечания.

1) Видим, что в общем случае может не выполняться закон коммутативности при умножении матриц, то есть

2) При умножении на матрицу, состоящую из всех единиц, исходная не получается, а вот если единицы по диагонали - получается. Матрица 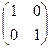называется единичной матрицей. При этом выполняется .

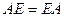Задача 5. Дана матрица 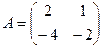найти .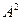

Решение. Умножим матрицу саму на себя, то есть две её копии напишем рядом и умножим их.

= =

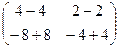= . Ответ. .

Как видно из этого примера, для матриц, в отличие от чисел, возможно, что получается нулевой объект в ответе, притом что в исходной матрице вообще ни одного нуля не было. Это из-за особенностей её строения: правый столбец в 2 раза меньше, чем левый, а нижняя строка в минус 2 раза больше, чем верхняя. И вообще, если взять пару матриц, где у первой будет пропорциональность строк (в k раз больше) а у второй - столбцов (в минус k раз меньше) получим такой же эффект.

Задача 6. Найти произведение матриц .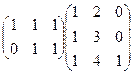

Решение. Размеры согласованы: длина строки 1-й матрицы равна высоте столбца 2-й матрицы. Первую можно мысленно разрезать на 2 строки, вторую на 3 столбца. Итого будет 6 различных произведений строк на столбцы.

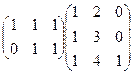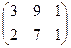= . Ответ. .

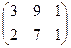Задача 7. Вычислить 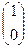и .

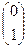Заметим, что получаются 1-й и 2-й столбец матрицы.

= , = .

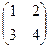
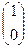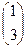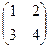
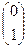Квадратная матрица отображает вектор в вектор. Коротко о понятии линейного оператора и строении его матрицы и о том, что при умножении на i-й базисный вектор получается столбец номер i.

Задача 8А. Найти произведение: .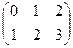

Задача 8Б. .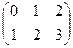

Решение. В 1-м случае размеры и , согласованы, умножение возможно. Во 2-м случае и 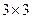, тоже согласованы (хоть столбцов и больше, но всё равно длина строки 1-й матрицы равна высоты столбца 2-й матрицы). Просто в ответе для 3Б получится ещё один лишний столбец справа.

= =

= .

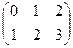
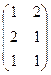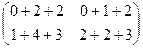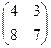Для 3Б 1-я и 2-я строка умножаются не только на 1-й и 2-й, но ещё и на 3-й столбец. Дополнительно получаем

= = .

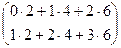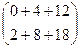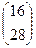Выделим красным цветом новый столбец:

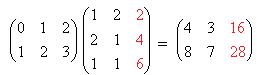
Ответ. 8А: 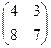, 8Б: .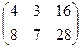

Задача 9. Даны матрицы

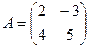, , . Найти .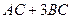

Решение. Так как матрица С находится справа во всех слагаемых, то для удобства можно использовать приведение подобных 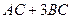= - тогда умножение надо будет проводить всего один раз, а не два.

Сначала запишем .

= = .

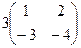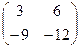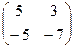Теперь умножим на матрицу С. Точно так же, как и в прошлом примере, мысленно обведём строку из 1-й матрицы на столбец из 2-й.

Есть 4 варианта это сделать:

= = = .

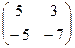
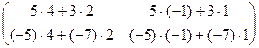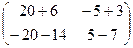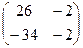Ответ. .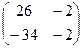

Задача 10. Даны матрицы 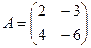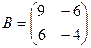. Найти .

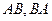Решение. = = .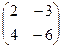

= = .

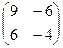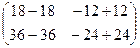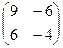
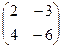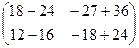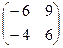Ответ. .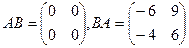

 

Задача 11. Найти произведение матриц .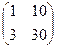

Решение. = = .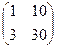

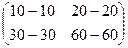Ответ. .

 

Задача 12. Даны матрицы:

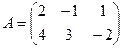
Найти .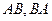

Решение.

= = .

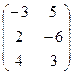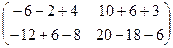Теперь поставим их наоборот, но при этом произведением будет уже не матрица 2 порядка, а матрица 3 порядка: теперь у первой 3 строки, но более коротких, а у второй 3 столбца. Вариантов умножить строку на столбец будет 9.

= = .

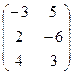
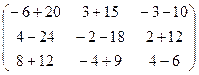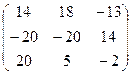Ответ. , .

Задача 13. Даны матрицы 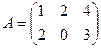. Найти .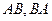

Решение.

= = .

= = .

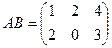
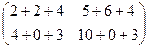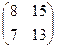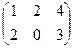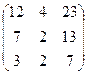Ответ. , .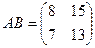

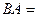
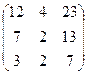Задача 14. Дана матрица 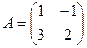. Найти .

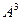Решение. Сначала умножим две, и найдём .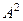

= = .

Теперь домножим ещё на одну матрицу А, чтобы найти .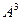

= = .

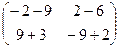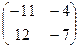Ответ. .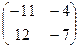

Замечание. Несмотря на то, что в общем случае коммутативности по умножению матриц нет, но если матрица 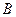совпадает с матрицей 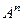, тогда 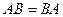. Например, в этой задаче, 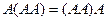из-за ассоциативности, т.е. неважно, домножить третий раз слева или справа.

 

Домашняя. Найти 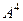для этой же матрицы. Замечание. Здесь есть 2 метода решения: либо умножить 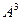, полученную в прошлой задаче, ещё раз на 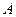, либо взять 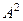, полученную на первом этапе, и её умножить саму на себя. Ответ. .

Задача 15. Найти произведени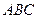е , где

, , .

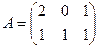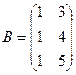Решение. Вычислим 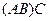, сначала умножим первые две матрицы:

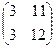= . Теперь умножим на третью матрицу.

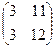
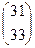= . Ответ. .

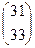Замечание. Если вычислять 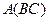, то получается точно такой же результат, т.к. выполняется закон ассоциативности.

 

Замечание. При умножении квадратной матрицы на вектор-столбец получается снова вектор-столбец, то есть квадратная матрица фактически выступает в роли функции, отображающей векторы в пространстве (или на плоскости, если n = 2).

 

Определители.

Задача 16. = .

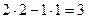Для параллелограмма, построенного на базе системы векторов (2,1) и (1,2), площадь равна 3. Если область 2’ перенести в область 2, то видно, что получается половина прямоугольника площади 2 (выделено жёлтым). То есть площадь равна 1. Аналогично 3’ в 3. Там тоже площадь 1. Кроме того, в центре квадрат площади 1.

Задача 17. Найти определитель .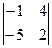

Решение. = .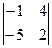

Ответ. 18.

 

Задача 18. Найти определитель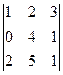

Решение. Допишем копии первых двух столбцов, проведём 3 параллельных линии (главная диагональ и ещё две). Перемножим все эти тройки элементов и внесём в общую сумму с их исходным знаком. А вот для побочной диагонали и линий, ей параллельных, со сменой знака.

=

.

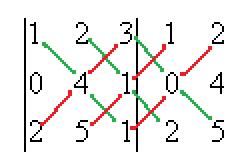
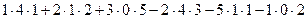Ответ. .

 

 

Задача 19. Найти определитель .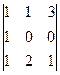

Решение.

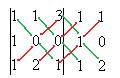
То, что перемножено по зелёным линиям, включим в сумму со знаком плюс, а по красным - со знаком минус.

= .

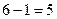Ответ. 5.

Задача 20. Найти определитель .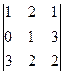

Решение.

. Ответ. 11.

Задача 21. Найти определитель .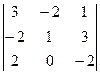

Решение.

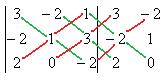
. Ответ. .

Задача 22. Найти определитель .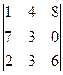

Решение.

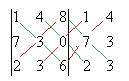
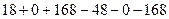= . Ответ. .

Задача 23. Вычислить определитель .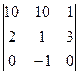

Решение. Аналогичным методом,

= .

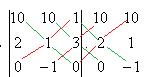
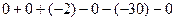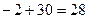Ответ. 28.

Задача 24. Вычислить определитель .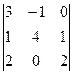

Решение. Заметим, что 1-й и 3-й столбец содержат очень похожие группы элементов а именно 1 и 2. Вычтем из 1-го столбца 3-й, а затем разложим по 1-му столбцу.

= = =

.

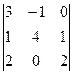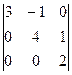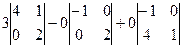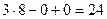Ответ. 24.

Задача 25. Вычислить определитель .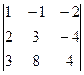

Решение. =

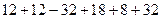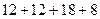= = 50.

Ответ. 50.

 

 

Задача 26. Найти параметр , при котором определитель равен 0:

.

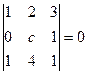Решение. Вычислим определитель и решим получившееся уравнение:

, , , .

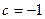Ответ. .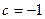

Задача 27. Найти параметр , при котором определитель равен 6:

.

Решение. Вычислим определитель и решим получившееся уравнение:

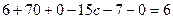
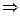
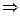
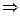
Ответ. 4,2.

 

Задача 28. Найти объём тетраэдра, вершины которого

A(1,1,1), B(2,1,3), C(2,2,4), D(1,2,4).

Решение. Объём тетраэдра ровно в 6 раз меньше объёма параллелепипеда с рёбрами AB, AC, AD.

Найдём эти векторы, и сначала вычислим объём параллелепипеда с помощью определителя, затем поделим на 6.

AB = (1,0,2), AC = (0,1,3), AD = (1,1,3).

= , .

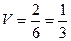Ответ. Объём тетраэдра равен .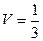

Задача 29. Вычислить определитель с помощью разложения по первой строке.

Решение. Выберем дополняющий минор для каждого элемента 1-й строки, и домножим на

=

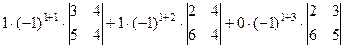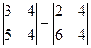= = 8. Ответ. 8.

Задача 30. Вычислить определитель 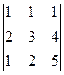методом Гаусса (приведением к треугольной форме).

Решение. Вычитаем из 2-й строки удвоенную 1-ю, и из 3-й 1-ю.

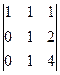= затем вычитаем из 3-й строки 2-ю.

получили 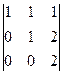= 2. Ответ. 2.

 

Задача 31. Вычислить определитель .

Решение. Прибавим 1-ю строку ко 2-й, 3-й и 4-й.

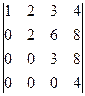. Эта матрица треугольная, определитель равен произведению чисел по диагонали, то есть 24.

Ответ. 24.

Задача 32 (а,б). Вычислить определитель 4 порядка двумя способами: а) разложением по 1-й строке. б) с помощью преобразований матрицы.

Решение. Первый способ.

Разложение по 1-й строке:

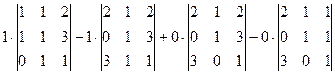
Очевидно, что последние 2 минора 3-го порядка вычислять не надо, так как они умножаются на 0. Осталось вычислить два минора 3 порядка, то есть мы свели определитель 4 порядка к определителям 3 порядка.

= .

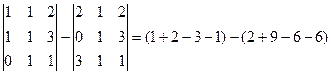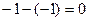Ответ. 0.

Второй способ. Из 2-го столбца вычтем 1-й

А теперь разложим по 1-й строке, причём реально для вычисления останется только один минор третьего порядка.

. Теперь ко 2-й строке прибавим 1-ю а из 3-й вычтем утроенную 1-ю. А затем уже к 3-й строке прибавляем 2-ю.

= = = 0.

Ответ. 0.

Задача 33. Вычислить определитель .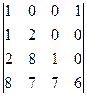

Решение. Можем разложить по 1-й строке (там всего 2 элемента отличны от 0). Но можно сначала упростить матрицу, а именно, отнять от 4 столбца 1-й столбец. Тогда в 1-й строке будет всего один ненулевой элемент. Также выносим 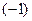из последнего столбца.

= = = =

= .

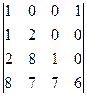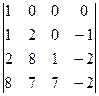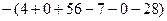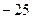Ответ. .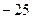

Задача 34. Вычислить определитель .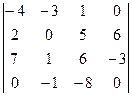

Решение. Наиболее удобно, если мы захотим применить метод Гаусса для упрощения матрицы, поставить число 1 в левый верхний угол. Сделаем это, поменяв местами 1 и 3 столбцы.

 

=

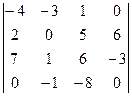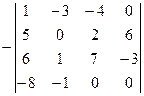
Меняя местами два столбца, должны домножить на 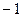, что и сделано.

Но теперь заметим ещё и тот факт, что в 4 стоке только отрицательные числа. Можно вынести коэффициент 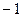их этой строки, и знак перед всем выражением снова станет + Итак:

В последней строке всего 2 числа из 4-х отличны от 0. Вычтем из 1-го столбца второй, умноженный на 8, чтобы в последней строке оставить лишь одно число. А потом разложим по последней строке.

= =

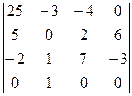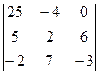
а этот определитель уже вычислим обычным путём, например, допишем копии 1 и 2 столбцов.

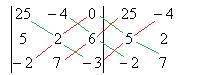
По зелёным линиям умножаем тройки чисел и не меняем знак, а по красным - меняем знак (изучали ранее этот метод).

= = .

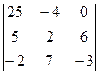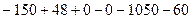Ответ. .

 

 

Обратная матрица.

Формула вычисления элементов обратной матрицы: .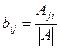

Алгоритм нахождения .

1. Проверить невырожденность с помощью определителя.

2. Составить матрицу из дополняющих миноров M_ij.

3. Изменить знаки в шахматном порядке, то есть домножить на (-1)^i+j, где i,j - номера строки и столбца.

4. Транспонировать полученную матрицу.

5. Поделить на определитель исходной матрицы.

Задача 35. Найти обратную матрицу для .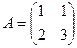

Решение. 1). Проверяем определитель , так что обратная матрица существует.

2) Составляем матрицу из дополняющих миноров, то есть для каждой клетки вычёркиваем строку и столбец, остаётся подматрица порядка 1, то есть то число, которое напротив, как раз и является дополняющим минором. Получаем .

3) В шахматном порядке меняем знак там, где i+j нечётное.

Тем самым, мы переходим от 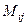к . Получили .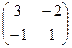

4) Транспонируем эту матрицу. .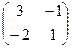

5) Определитель был равен 1. Делить на 1 не обязательно, можно автоматически считать, что уже и так разделили.
Ответ. .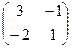

Проверка: = = .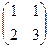

 

 

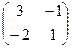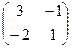
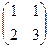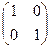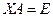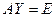Минута теории. Докажем, что не существует различных матриц «обратной слева» и «обратной справа». Так как коммутативность в общем случае не выполняется, то вовсе не очевидно, что обратная матрица единственна, можно предположить, что левая обратная и правая обратная - различны. Докажем, что если и , то .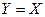

Доказательство. Пусть 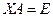и .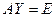

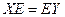По закону ассоциативности, можно записать такое равенство: . Но тогда получается , то есть .

 

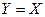Перейдём к задачам с матрицами 3 порядка.

Задача 36. Найти обратную матрицу .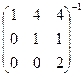

Решение. Сначала ищем определитель. Так как матрица треугольная, то достаточно перемножить числа по диагонали. .

Строим матрицу, состоящую из дополняющих миноров.

Зачёркиваем ту строку и тот столбец, где находится элемент, и остаётся минор 2 порядка из 4 элементов.

На схеме показано, что именно надо зачеркнуть:

= = .

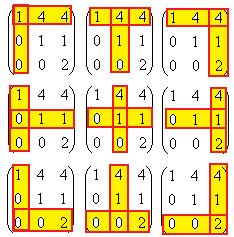
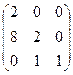Теперь надо сменить знаки в шахматном порядке, т.е. переходим от миноров к алгебраическим дополнениям. Обведено красным, где надо менять знак. Ясно, что 0 остаётся 0, там знак менять нет смысла.

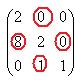
Получили: = .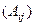

Транспонируем эту матрицу, то есть бывшие строки запишем по столбцам.

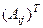= . И осталось разделить на .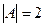

Ответ. .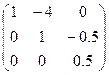

Задача 37. Найти обратную матрицу .

Решение. Найдём определитель

.

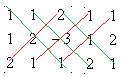
Найдём матрицу из дополняющих миноров к каждой из 9 клеток.

= = .

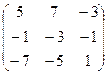Меняем знаки в шахматном порядке, то есть там, где i+j нечётное.

= .

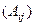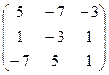Затем транспонируем эту матрицу.

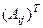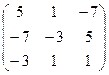= . Осталось только разделить на .

Ответ. .

Задача 38. Найти обратную матрицу .

Решение. Сначала находим определитель.

.

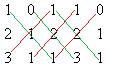
Найдём матрицу из дополняющих миноров.

= = .

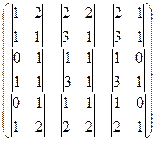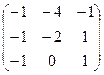Меняем знаки в шахматном порядке, там, где i+j нечётное.

= .

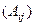Затем транспонируем эту матрицу.

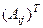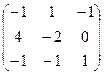= . Затем делим на .

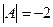Ответ. = .

Задача 39. Матричным методом решить систему уравнений:

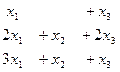
Решение. Запишем систему в виде: .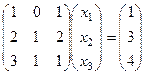

Обратите внимение, что основная матрица системы это та самая матрица, для которой мы нашли обратную в прошлой задаче.

Если у нас есть равенств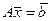о , то 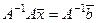, тогда .

=

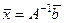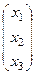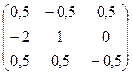
Поделиться: