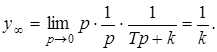Реферат
на тему:
"Интегральные методы оценки качества переходных процессов"
Введение
Интегральная оценка является обобщенным показателем качества переходного процесса, при этом качество системы оценивается с помощью числа, являющегося интегралом некоторой функции.
Особенность интегральной оценки в том, что в отличии от других методов оценки качества, величина интеграла представляет число, которое ничего не говорит о характере переходного процесса, о конкретных показателях качества, зато, в сравнении с другими, метод отличается простотой.
Линейная интегральная оценка
Рассмотрим переходные процессы, приведенные на рис. 1а-в.

А б в
Рис. 1
Заштрихованная площадь называется площадью регулирования, она может быть оценкой качества переходного процесса. Чем меньше площадь, тем лучше качество переходного процесса.
Площадь регулирования может быть определена с помощью интеграла, который называется простой (линейной) интегральной оценкой
 (1)
(1)
Задача сводится к определению J1, не зная переходного процесса, т.е. по его изображению, так как изображение проще определить.
Пусть известно
 (1)
(1)
Если сравнивать выражения (1) и (2), то они отличаются на множитель e-pt. При этом
 , (3)
, (3)
т.е. получили простую формулу для определения площади регулирования, а значит и оценки качества процесса регулирования.
Так как z(p) = y(p) – y¥ /p, то значение интеграла (1) можно вычислить по формуле
 (4)
(4)
Недостаток метода
Рассмотрим переходный процесс (рис. 2).

Рис. 2
Процесс затухает медленно, следовательно, качество системы плохое, но так как площади имеют разные знаки, то величина интеграла J1 будет мала. Поэтому этот метод не применим для колебательных переходных процессов, т.е. он пригоден только для монотонных процессов, поэтому ограничен в применении.
Хорошей оценкой мог бы служить интеграл
 , (5)
, (5)
Но его сложно вычислять, необходимо решать характеристическое уравнение.
Пример 5. Вычислить величину J1 для заданной системы (рис. 3).
| |||
 | |||
Рис. 3
3. Определим величину интеграла J1

Интегральная квадратичная оценка
Интегральная квадратичная оценка пригодна для любых переходных процессов, и вычисляется по формуле
 (6)
(6)
Подинтегральное выражение – z2(t) всегда положительно не зависимо от знака функции z(t).
Определим J2 без расчета переходного процесса, для этого воспользуемся дуальной теоремой.

Рис. 4
Основная теорема: произведению изображений соответствует свертка оригиналов
 (7)
(7)
Дуальная теорема: произведению оригиналов соответствует свертка изображений
 (8)
(8)
Так как 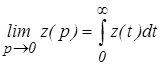 ,
,
то можно получить следующую формулу для расчета квадратичной интегральной оценки
 (9)
(9)
Этот интеграл можно вычислить либо с помощью вычетов по полюсам подинтегральной функции, либо с использованием табулированных значений интеграла для функции
 (10)
(10)
В таблице 1 приведены табулированные значения интеграла для n = 1 ¸ 3 для систем более высокого порядка таблицы приведены в литературе [5].
Таблица 1
| n | J2 |

| |

| |
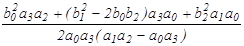
|
Недостаток метода. Рассмотрим переходные процессы (рис. 5).

а) б)
Рис. 5
При использовании этого метода два процесса могут иметь одинаковую площадь регулирования, но оба они плохие по различным показателям качества, у первого большое время регулирования, а во втором большое перерегулирование.
Пример 6. Вычислить величину J2 для заданной системы (рис. 6).
 | |||
| |||
Рис. 6
3. Определим z(p)

4. Определим величину интеграла J2 с помощью вычетов s1 = – k/T


5. Определим величину интеграла J2 с помощью таблиц

Модифицированная интегральная оценка
При использовании модифицированной (улучшенной) интегральной оценки минимизируем не только квадратичное отклонение z(t), но и его производную – z’ (t). Такой оценкой является интеграл
 (11)
(11)
где t – постоянная времени.
Минимуму интеграла соответствует приближение переходного процесса не к ступенчатому, а к некоторому экспоненциальному с заданной постоянной времени (которая называется экстремалью). Применение этой оценки приводит к более пологим переходным процессам, т.е. менее колебательным и имеющим меньшее число перерегулирований.
 2. Определим y¥
2. Определим y¥


 2. Определим y¥
2. Определим y¥