Задачник
Индивидуальных заданий по курсу «Начертательная геометрия»
Составили: Нестеров П.А.
Якушев В.А.
Бабин С.В.
Москва 2003
Якушев Виктор Александрович
Нестеров Павел Анатольевич
Бабин Сергей Васильевич
Утверждено методическим советом кафедры «Материаловедение и пластическая деформация металлов»
Подпись в печать объемом 2 п.л. тираж 60 экз.
Введение
Сборник задач по Начертательной геометрии представлен в виде тетради, на которой спроецированы геометрические фигуры. По проекциям необходимо представить пространственное расположение геометрических фигур и решить задачу на проекциях. По сравнению с перечерчиванием и последующим решением задач данный метод является более прогрессивным, и количество решаемых задач на практических занятиях и самостоятельных возрастет и, следовательно, развитие пространственного мышления будет проходить быстрее.
Методические указания к выполнению задач
По курсу «Начертательная геометрия»
Методические указания выполнены в виде тетради, на которой необходимо выполнять решение задач. Решение задач выполнять в карандаше с записью алгоритма решения. Объем задач соответствует объему материала изучаемого в данном курсе.
Сборник задач представлен в виде тетради с которой студент для себя должен сделать копию и проводить решение задач в ней или перечертить в тетрадь в эскизном варианте (т.е. перечертить в тетрадь с примерным расположением геометрических объектов).
Второй способ хранения информации - электронная версия данных задач, с которой студент может сделать копию и решать задачи на компьютере.
Решение на компьютере необходимо проводить в графическом пакете «AutoCAD», причем эти решения можно рассматривать и в пространственной модели. Для контроля правильности выполнения решения задач студент может обратиться в компьютерный класс и проверить решение данной задачи.
ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ И ПРОСТЕЙШИЕ СИМВОЛЫ
(AB) – прямая AB.
[ AB ] – отрезок AB.
[ AB) – луч AB.
│AB│- длина отрезка AB.
{ AB } – множество с элементами A и B.
Ø – пустое множество.
A Î Φ – точка A принадлежит фигуре Φ.
Φ Î Φ1 – фигура Φ принадлежит Φ1.
A Ï Φ – точка A не принадлежит фигуре Φ.
Φ1 Ï Φ – Φ1 не является подмножеством Φ.
Φ1 = Φ – фигуры Φ1 и Φ совпадают.
Φ1 ≠ Φ – фигуры Φ1 и Φ не совпадают.
Φ1 ≈ Φ - фигуры Φ1 и Φ конгруэнтны.
Φ1 U Φ2 - объединение Φ1 и Φ2.
Φ1 ∩ Φ2 - пересечение Φ1 и Φ2.
↑↑ - сонаправленные /лучи и векторы/.
↑↓ - противоположно направленные.
|| - параллельные.
|| - не параллельные.
┴ - перпендикулярные.
??? – скрещивающиеся.
Ð – угол.
^ - величина угла.
=> - следует.
П 1 – горизонтальная плоскость проекций.
П 2 - фронтальная плоскость проекций.
П 3 – профильная плоскость проекций.
X; Y; Z – оси проекций.
О – начало координат.
Точки /оригиналы/ A, B, C, ……, K, M.
Проекции точек: горизонтальная – A1, B1, C1, ……, K1, M1.
фронтальная – A2, B2, C2, ……, K2, M2.
профильная – A3, B3, C3, ……, K3, M3.
выполненная аксонометрическим методом или
принадлежащая произвольной плоскости
проекций – A’, B’, C’, ……, K’, M’.
Линии /оригиналы/ - ℓ, k, m.
Их проекции /ℓ1, k1, n1/, /ℓ2, k2, n2/, /ℓ3, k3, n3/.
Проекции [ AB ]: горизонтальная – [ A1B1 ];
фронтальная – [ A2B2 ];
профильная - [ A3B3 ].
Плоскости обозначаются буквами, символизирующими элементы, которыми задана плоскость, например: ((АВ), (СК)), (А, (ВС)), (А, В, С); строчными буквами – α, β, γ.
Проекции плоскостей соответственно:
((А1 В1 ), (С1 К1)), (А2, (В2 С2)), (А1, В1, С1).
(α1, α2, α3 ), (β1, β2, β 3 ), (γ1, γ2, γ3).
α (А ∩ В); α (∆ АВС) …….
ПРОЕЦИРОВАНИЕ
Свойства параллельного проецирования
ЗАДАЧА № 1
Построить параллельные проекции заданных геометрических образов, приняв q за направление проецирования.


ЗАДАЧА № 2
Треугольник A1B1C1 – параллельная проекция правильного треугольника.
Построить проекции высот этого треугольника.

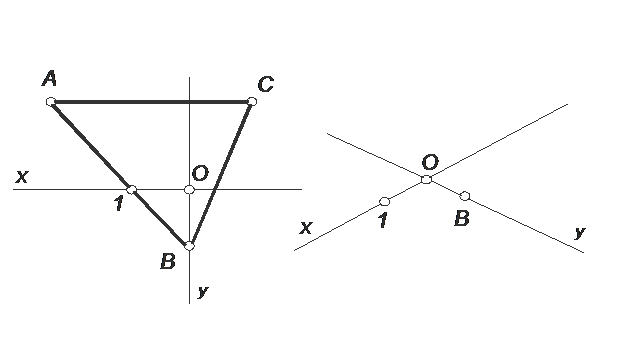
ЗАДАЧА № 3
Построить параллельную проекцию ∆ АВС / ĀВС /, отнесённого к прямоугольной системе координат x0y, если параллельная проекция системы координат и точек 1 и В задана.
ЗАДАЧА № 4
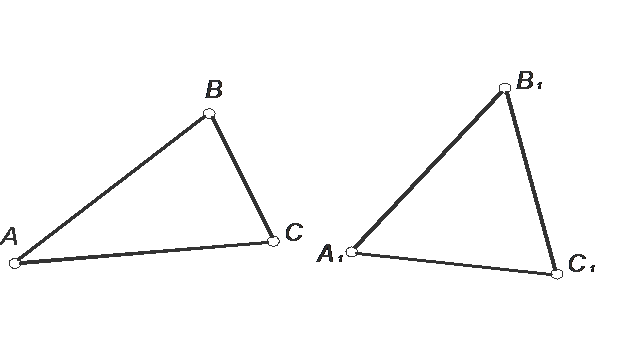
Треугольник A1B1C1 – изображение ∆ АВС. Выяснить, в косоугольной или прямоугольной проекции оно выполнено.
ЗАДАЧА № 5
Построить параллельную проекцию правильного шестиугольника.
Проекция треугольного отсека задана.

ЗАДАЧА № 6
Построить параллельную проекцию трапеции АВСК, если известно, что соотношение длин оснований трапеции │СК│: │АВ│ = 2:5 и изображение
[CK] задано.

ПОСТРОЕНИЕ ИЗОБРАЖЕНИЙ ПО МЕТОДУ КОМПЛЕКСА ПРОЕКЦИЙ /КП/
КП точки
ЗАДАЧА № 7
По заданному наглядному изображению построить КП точек А, В, С и D.

ЗАДАЧА № 8
Достроить недостающие проекции точек при условии, что глубина точки А равна 20 мм, а точки В – 5мм и что высота точки С равна 50мм, а точки D – 30мм. Построить наглядное изображение заданных точек.

ЗАДАЧА № 9
По заданному КП определить глубину / y /, высоту / z / и ширину / x / точек.
Результаты занести в таблицу. Построить наглядное изображение всех точек.

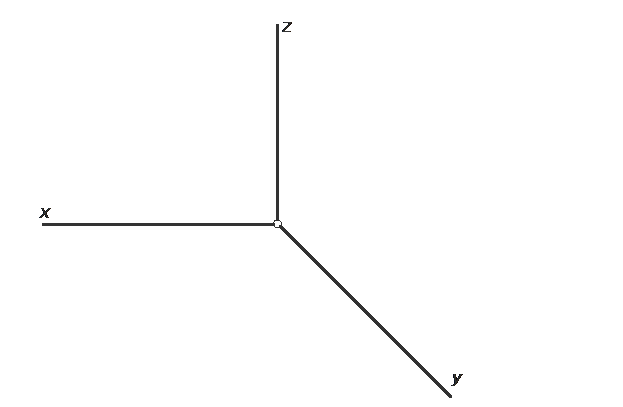
ЗАДАЧА № 10
Построить наглядное изображение параллелепипеда, вершины которого:
О – в начале координат; D - на плоскости П2;
А - / 30, 20, 25 /; E - на оси y;
В – на плоскости П1; F - на плоскости П3;
С – на оси x; G - на оси z.
На наглядном изображении показать все проекции вершин.

Записать координаты вершин параллелепипеда и построить для них КПпрямой.


КП ПРЯМОЙ
ЗАДАЧА № 11
Построить три проекции прямых DF, BF, BD, AB, DE и GB
/ из задачи №10 /. Указать расположение каждой прямой и её название.


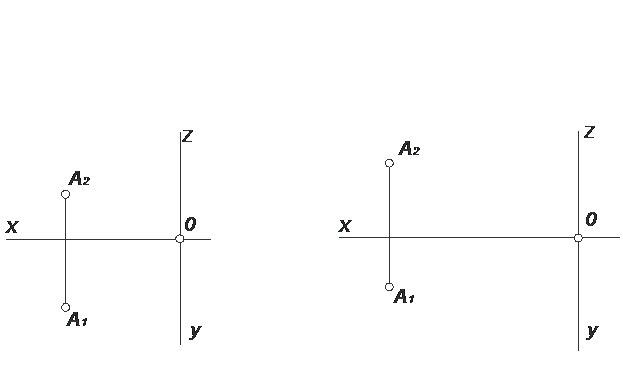
ЗАДАЧА № 12
Через точку А провести отрезок прямой АВ, если:
а/ Отрезок АВ упирается в б/ Отрезок АВ упирается в
плоскости П1 и П3 на расстоя- плоскости П2 и П3 на расстоя-
нии 5 мм от плоскости П2; нии 10 мм от плоскости П1;
 в/ Точка В удалена от всех г/ Точка В удалена от плоскостей П2 и П3
в/ Точка В удалена от всех г/ Точка В удалена от плоскостей П2 и П3
трёх плоскостей на 15 мм; на такое же расстояние, как и точка А, и
на 10 мм от плоскости П1.

ЗАДАЧА № 13
Указать расположение каждой из заданных точек K, L, F, D и E относительно прямой АВ / на прямой, выше, ниже, перед, за /.

ЗАДАЧА № 14
Построить недостающую проекцию точки С:
а/ Принадлежащую б/ Расположенную в/ Расположенную
прямой АВ; перед прямой АВ; за прямой АВ.

ЗАДАЧА № 15
Построить проекции точки С, делящей отрезок АВ в заданном отношении:
а/ АС: СВ = 2: 3; б/ АС: СВ = 2: 5.

ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ
ЗАДАЧА № 16
Через точку С провести прямую СК, параллельную прямой АВ:
а/ б/

ЗАДАЧА № 17
На двух прямых AB и CD найти конкурирующие точки:
а/ горизонтально; б/ фронтально.
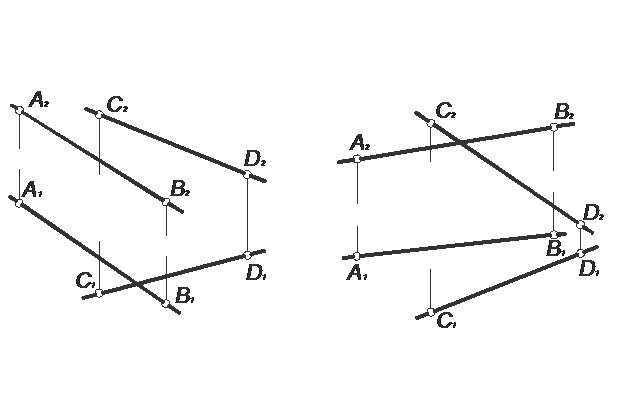
ЗАДАЧА № 18
Определить взаимное положение прямых АВ и СК:
а/ ……………………… б/ …………………………

ЗАДАЧА № 20
В заданной плоскости построить линии уровня:
а/ б/

ЗАДАЧА № 21ЗАДАЧА № 22
Установить, является ли Построить недостающую
изображённая фигура плоской. проекцию плоского много-
угольника.

ЗАДАЧА № 23
Построить проекции прямой КМ, лежащей в плоскости АВС, для которой заданы разноимённые проекции её концов:
а/ б/

ЗАДАЧА № 24
Построить недостающую проекцию треугольника АВС, лежащего в плоскости, заданной параллельными прямыми:
а/ б/ 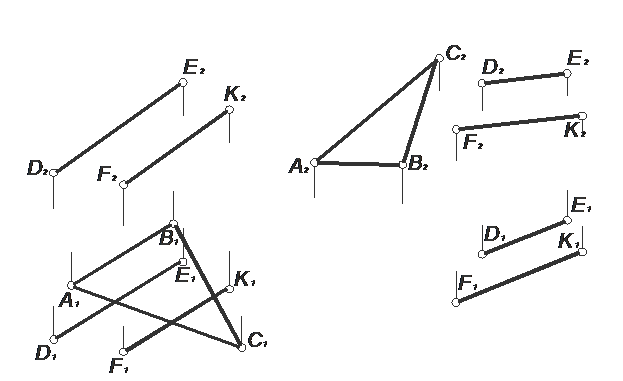
КП КРИВЫХ ЛИНИЙ
ЗАДАЧА № 25
Определить по заданному КП линии, плоская эта линия или пространственная.

ЗАДАЧА № 26
Плоская кривая ℓ задана горизонтальной проекцией и точками А, В и С. Построить её фронтальную проекцию.
. 
ЗАДАЧА № 27
Построить проекции винтовой линии / радиус цилиндра – носителя R=15
и высота подъёма Н=40/.
КП ПОВЕРХНОСТЕЙ
КП МНОГОГРАННИКОВ
ЗАДАЧА № 28
Построить очертания проекции пирамиды с вершиной S и основанием ABCDE. Определить видимость рёбер и построить недостающую проекцию точки 1, принадлежащей пирамиде:
а/ б/

ЗАДАЧА № 29
Построить три проекции наклонной призмы по заданным основанию АВС и ребру АА’. Определить видимость рёбер призмы.

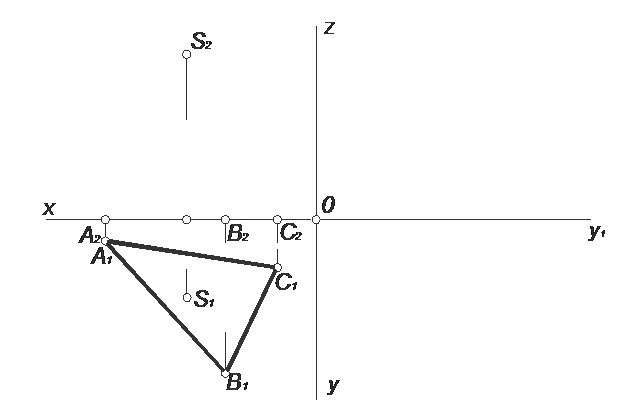
ЗАДАЧА № 30
Построить три проекции пирамиды по заданным основанию АВС и вершине S. Определить видимость рёбер пирамиды.
КП КРИВЫХ ПОВЕРХНОСТЕЙ
ЗАДАЧА № 31
Построить очертания проекций конической поверхности на П1 и П2 и вторую проекцию кривой СЕ, принадлежащей этой поверхности.

ЗАДАЧА № 32
Построить очертания проекций цилиндрической поверхности на П1 и П2 и вторую проекцию кривой СЕ, принадлежащей этой поверхности.

ЗАДАЧА № 33
Построить очертания проекций поверхности и фронтальную проекцию
точки М / по М1 /, принадлежащей:
а/ Прямому геликоиду / ось JJ, радиус цилиндра – носителя R и высота подъёма винтовой направляющей Н /;
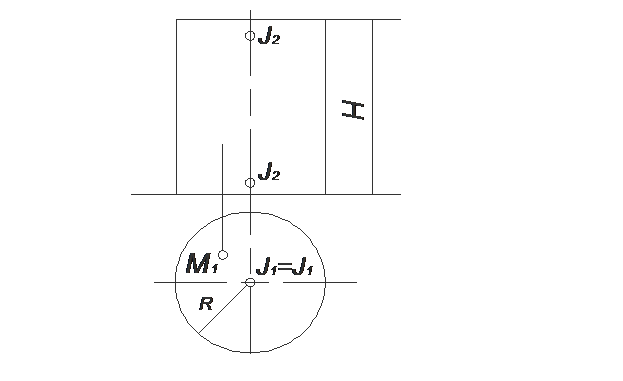
б/ Наклонному геликоиду / ось JJ, радиус цилиндра – носителя R, высота подъёма винтовой направляющей Н и угол наклона образующей базового конуса к оси 60° /.
