Пусть последовательность ненулевых комплексных чисел (не обязательно различных) - 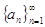 удовлетворяет условию
удовлетворяет условию
 ,
,  ,
,  . (51)
. (51)
Рассмотрим произведение(произведение Бляшке)
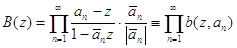 . (52)
. (52)
Для фиксированного  ,
,  , при
, при  имеет место оценка
имеет место оценка
 . (53)
. (53)
Так как ряд (51) сходится, то из (53) легко вывести, что произведение (52) сходится абсолютно и равномерно в круге  , т.е. функция
, т.е. функция  аналитична в единичном круге и имеет нули в точках
аналитична в единичном круге и имеет нули в точках 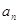 ,
,  , и только в этих точках. При этом, пользуясь неравенством
, и только в этих точках. При этом, пользуясь неравенством  (
( ,
,  ), мы находим
), мы находим
 ,
,  . (54)
. (54)
Допустим теперь, что  (
( ) - нули некоторой функции
) - нули некоторой функции 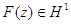 с
с  , причем каждый из них повторяется со своей кратностью. Докажем, что ряд (51) сходится. Положим
, причем каждый из них повторяется со своей кратностью. Докажем, что ряд (51) сходится. Положим
 ,
, 
Функция  (
( ) аналитична в круге радиуса больше единицы, и
) аналитична в круге радиуса больше единицы, и  , если
, если  . Следовательно,
. Следовательно,  и согласно п.3 теоремы 4
и согласно п.3 теоремы 4  . Но тогда
. Но тогда

и
 ,
,  (55)
(55)
Так как  ,
,  , то из (55) вытекает сходимость произведения
, то из (55) вытекает сходимость произведения  , а значит, и сходимость ряда (51).
, а значит, и сходимость ряда (51).
ОпределениеI.6.
Пусть 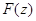 - аналитическая в круге
- аналитическая в круге  функция и
функция и 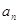 ,
,  (
( ) - ее нули, повторяющиеся со своей кратностью. Пусть также
) - ее нули, повторяющиеся со своей кратностью. Пусть также  - кратность нуля функции
- кратность нуля функции  при
при  . Произведение
. Произведение
 (56)
(56)
называется произведением Бляшке функции 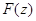 .
.
Справедлива
Теорема 6.
Каждая функция 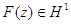 представима в виде
представима в виде
 ,
,
где  не имеет нулей в круге
не имеет нулей в круге  и
и
 ,
,  ,
,
а  - произведение Бляшке функции
- произведение Бляшке функции 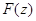 .
.
Доказательство.
Пусть 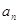 ,
,  (
( ) - нули функции
) - нули функции  (или, что то же самое, нули функции
(или, что то же самое, нули функции  ) Тогда, как отмечалось выше,
) Тогда, как отмечалось выше,  - аналитическая в круге
- аналитическая в круге  функция и
функция и
 ,
,  . (57)
. (57)
При этом функция  также аналитична в единичном круге, не имеет в нем нулей и
также аналитична в единичном круге, не имеет в нем нулей и  .
.
Для доказательства обратного неравенства рассмотрим частные произведения (56):
 ,
,  ,
,  .
.
Так как 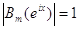 для любого
для любого  , то по теореме 4
, то по теореме 4

и
 , если
, если  .
.
Устремив в последнем неравенстве число m к бесконечности и учитывая, что  (
( ) равномерно по
) равномерно по  , мы получим
, мы получим
 ,
,  ,
,
т.е.  ,
,  .
.
Теорема 6 доказана.
ОпределениеI.7.
Пусть  ,
,  , - произвольное число. Обозначим через
, - произвольное число. Обозначим через 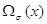 ,
,  , область, ограниченную двумя касательными, проведенными из точки
, область, ограниченную двумя касательными, проведенными из точки 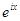 к окружности
к окружности 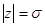 , и наибольшей из дуг окружности, заключенных между точками касания (при
, и наибольшей из дуг окружности, заключенных между точками касания (при 
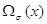 вырождается в радиус единичного круга). Для
вырождается в радиус единичного круга). Для  положим
положим
 ,
,  ,
,
где  - интеграл Пуассона функции
- интеграл Пуассона функции 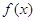 . Функция
. Функция  называется нетангенциальной максимальной функцией для
называется нетангенциальной максимальной функцией для 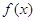 .
.
В силу теоремы 2
 для п.в.
для п.в.  . (58)
. (58)
Установим, что для произвольной функции  величина
величина  не превосходит (по порядку) значения максимальной функции
не превосходит (по порядку) значения максимальной функции  *) в точке х, т.е.
*) в точке х, т.е.
 ,
,  . (59)
. (59)
Нам понадобится
утверждение 3.
а) если функция  , то для любого
, то для любого 
 ;
;
б) если функция  ,
,  то
то  ,
,
где  - постоянная, зависящая только от числа р.
- постоянная, зависящая только от числа р.
Пусть  и
и  . По определению интеграла Пуассона
. По определению интеграла Пуассона

Положим 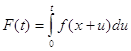 . Тогда будем иметь
. Тогда будем иметь

и, в силу неравенства  ,
,  , и периодичности
, и периодичности  ,
,
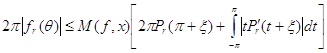 . (60)
. (60)
Так как обе функции  и
и  положительны при
положительны при  и отрицательны при
и отрицательны при  (из (5)), то, предполагая без ограничения общности, что
(из (5)), то, предполагая без ограничения общности, что  , мы получим
, мы получим
 . (61)
. (61)
Для  имеют место оценки
имеют место оценки
 ,
,
 .
.
Следовательно, для доказательства неравенства (59) достаточно проверить, что
 при
при  , (62)
, (62)
если  . Пусть
. Пусть  , тогда
, тогда
 .
.
В остальных случаях неравенство (62) очевидно. Из (58), (59) и утверждения 3 вытекает, что для любой функции  ,
, 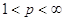 ,
,
 , (63)
, (63)
где  - постоянная, зависящая только от
- постоянная, зависящая только от  .
.
Теорема 7.
Пусть  (
( ),
),  и
и
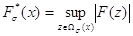 ,
,  .
.
 Тогда
Тогда  и
и
 . (64)
. (64)
Доказательство.
Утверждение теоремы 7 в случае, когда 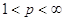 , есть прямое следствие оценки (63) и теоремы 4. Пусть теперь
, есть прямое следствие оценки (63) и теоремы 4. Пусть теперь 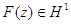 . По теореме 6
. По теореме 6  , где
, где  ,
,  , если
, если  и
и  . Из функции
. Из функции  можно извлечь корень: существует функция
можно извлечь корень: существует функция  такая, что
такая, что  , и, следовательно из (64) при р=2, получим
, и, следовательно из (64) при р=2, получим
 .
.
Оценка снизу для  вытекает из (58).
вытекает из (58).
Теорема 7 доказана.