с помощью разложения на элементарные дроби.

Раздел 3. Неопределенный интеграл.

Тема 3.1. Интегрирование по частям.

Контрольные вопросы

1) Свойства неопределенного интеграла. - Первообразной функции y=f(x), заданной на некотором интервале (a,b), называется любая функция F(x), производная которой в любой точке данного интервала равна f(x):
F′(x)=f(x).
Если F(x) является первообразной функции f(x), то функция вида F(x)+C, где C − произвольная постоянная, также является первообразной для f(x).

1. Неопределенным интегралом функции f(x) называется совокупность всех первообразных этой функции:
∫f(x)dx=F(x)+C, если F′(x)=f(x).

2. Производная неопределенного интеграла равна подынтегральной функции:
(∫f(x)dx)′=f(x).

3. Интеграл суммы функций равен сумме интегралов:
∫[f(x)+g(x)]dx=∫f(x)dx+∫g(x)dx.

4. Интеграл разности функций равен разности интегралов:
∫[f(x)−g(x)]dx=∫f(x)dx−∫g(x)dx.

5. Постоянный коэффициент можно выносить за знак неопределенного интеграла:
∫kf(x)dx=k∫f(x)dx.

6. ∫f(ax)dx=1aF(ax)+C

7. ∫f(ax+b)dx=1aF(ax+b)+C

8. ∫f(x)f′(x)dx=12f2(x)+C

9. ∫f′(x)f(x)dx=ln|f(x)|+C

10. Метод подстановки
∫f(x)dx=∫f(u(t))u′(t)dt,если x=u(t).

11. Метод интегрирования по частям
∫udv=uv−∫vdu,

где u(x), v(x) − дифференцируемые функции.

2) Таблица основных интегралов. –

№	Интеграл	Значение	№	Интеграл	Значение
	ò dx	x+C
		–

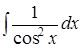
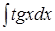
3) Метод интегрирования по частям.

Вспомним формулу производной произведения:

где u и v – некоторые функции от х. В дифференциальной форме:

Проинтегрировав, получаем: , а в соответствии с приведенными выше свойствами неопределенного интеграла:

или ;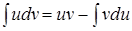

Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.

При использовании метода по частям за u берется такая функция, которая при дифференцировании упрощается, а за dv – та часть подынтегрального выражения, интеграл от которой известен или может быть найден.

Большую часть интегралов, вычисляемых по частям, можно разбить на три группы:

1. Интегралы вида 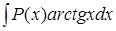, , , , , где P (x) – многочлен. Для их вычисления следует за u принимать одну из вышеуказанных функций, а dv = P (x) dx.

2. Интегралы вида , , , где P (x) – многочлен, а a – некоторое число. Для их вычисления следует приять u = P (x), а dv = e^axdx, dv = sin axdx, dv = cos axdx.

Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.

3. Интегралы вида , , где a и b – некоторые числа. Эти интегралы вычисляются двукратным интегрированием по частям.

Интегрирование рациональных дробей

с помощью разложения на элементарные дроби.

Контрольные вопросы

1) Интегрирование рациональных дробей с помощью разложения на простейшие дроби.

Найти неопределенный интеграл. Выполнить проверку.

Начинаем подбирать числитель.

Алгоритм подбора числителя примерно такой:

1) В числителе мне нужно организовать , но там . Что делать? Заключаю в скобки и умножаю на : .

2) Теперь пробую раскрыть эти скобки, что получится? . Хмм… уже лучше, но никакой двойки при изначально в числителе нет. Что делать? Нужно домножить на :

3) Снова раскрываю скобки: . А вот и первый успех! Нужный получился! Но проблема в том, что появилось лишнее слагаемое . Что делать? Чтобы выражение не изменилось, я обязан прибавить к своей конструкции это же :
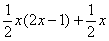. Жить стало легче. А нельзя ли еще раз в числителе организовать ?

4) Можно. Пробуем: . Раскрываем скобки второго слагаемого:
. Простите, но у меня вообще-то было на предыдущем шаге , а не . Что делать? Нужно домножить второе слагаемое на :

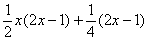
5) Снова для проверки раскрываю скобки во втором слагаемом:
. Вот теперь нормально: получено 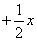из окончательной конструкции пункта 3! Но опять есть маленькое «но», появилось лишнее слагаемое , значит, я обязан прибавить к своему выражению :

Если всё выполнено правильно, то при раскрытии всех скобок у нас должен получиться исходный числитель подынтегральной функции. Проверяем:
Гуд.

Таким образом:

Готово. В последнем слагаемом я применил метод подведения функции под дифференциал.

2) Метод неопределенных коэффициентов.

Задание	Выполнить деление многочлена на многочлен
Решение	Поделим многочлен на многочлен уголком: То есть
Ответ