ОбразЦЫРЕШЕНИЯ ЗАДАЧ НА РАСЧЕТ ОДНОФАЗНЫХ И ТРЕХФАЗНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА.
Пример решения задачи на расчет неразветленной цепи.
Задача: Последовательно с катушкой, активное сопротивление которой R 1=10 Ом и индуктивность L =0,0318 Гн, включен приемник, обладающий активным сопротивлением R 2 = 1 Ом и емкостью С =796 мкф (рис. I). К цепи приложено переменное напряжение, изменяющееся по закону u =169,8·sin(314· t).
 |

Рис. 1.
Определить: полное сопротивление цепи, коэффициент мощности цепи, ток в цепи, активную, реактивную и полную мощности, а также построить в масштабе векторную диаграмму.
Как нужно изменить величину емкости, чтобы в цепи наступил резонанс напряжений? Индуктивность катушки остается постоянной.
Решение:
1. Сравнивая закон изменения напряжения о цепи с общим выражением u=U M·sin(ωt), можно заключить, что амплитуда напряжения U M=169,8 B, а ω =2 π·f =314 (1/сек).
Отсюда действующее значение напряжения

Частота тока

2. Индуктивное сопротивление катушки
X L= ωL= 2 π·f·L= 2·3.14·50·0.0318=10 Ом.
3. Емкостное сопротивление конденсатора

4. Полное сопротивление цепи

5. Коэффициент мощности цепи
 φ =28,35ْ
φ =28,35ْ
6. Сила тока в цепи

7. Активная мощность
P=I2 (R 1+ R 2)=9.62(10+1)=1014 Bт.
или
P=U·I· cos φ = 120·9.6·0.88=1014 Вт.
8. Реактивная мощность
Q = I2X L- I2X C= I2 (X L- X C)=9.62(10-4)=553 Вар.
или
Q=I·U· sin φ =120·9.6·0.49=553 Вар.
9. Полная мощность
S=I2z= 9.62·12.5=1152 ВА
или
S=U·I= 120·9.6=1152 BA
или

10. Построение векторной диаграммы начинаем с определения потерь напряжений на каждом сопротивлении:
U R1= I·R 1=9.6·10=96(В);
U R2= I·R 2=9.6·1=9.6(В);
U L= I·X L=9.6·10=96(В);
U C= I·X C=9.6·4=38.4(В);
|
|
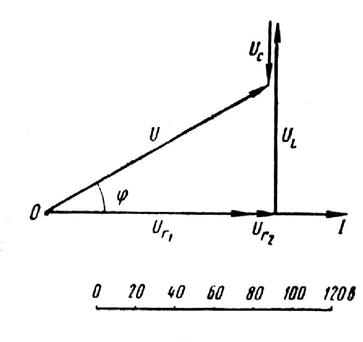
Рис.2
Затем выбираем масштаб для напряжений (см. рис. 2). Построение диаграммы начинаем с вектора тока I, который откладываем по горизонтали вправо от точки О (рис. 2). Вдоль вектора тока откладываем в принятом масштабе напряжения UR1 и UR2 теряемые в активных сопротивлениях цепи. Эти напряжения совпадают по фазе с током. От конца вектора UR2 откладываем в сторону опережения вектора тока под углом 90° вектор потери напряжения U L в индуктивном сопротивлении. Из конца вектора U L откладываем вектор U C в сторону отставания от вектора тока на угол 90°. Геометрическая сумма четырех векторов равна полному напряжению, приложенному к цепи, т. е.
U=U R1 +U R2 +U L +U C.
11. Для получения резонанса напряжений необходимо, чтобы Х C =Х L=10 Ом, тогда  , откуда
, откуда  При этом ток в цепи станет
При этом ток в цепи станет  , где
, где 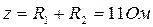 .
.
Пример решения задачи на расчет разветвленной цепи.
Задача: Катушка с активным сопротивлением R =20 Oм и индуктивностью L =0,0637 Гн соединена параллельно с конденсатором емкостью С =65 мкФ (рис. 3).
Определить: токи в ветвях и в неразветвленной части цепи, активные мощности ветвей, углы сдвига фаз между током и напряжением первой и второй ветвей и всей цепи, если к цепи приложено напряжение U =100B, частота тока f =50 Гц. Как нужно изменить емкость во второй ветви, чтобы в цепи наступил резонанс токов?
|
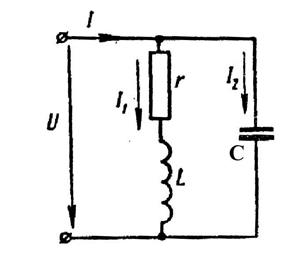
Рис.3.
Построить векторную диаграмму.
Решение:
1. Индуктивное сопротивление катушки
X L= ωL= 2 π·f·L= 2·3.14·50·0.0637 = 20 Ом.
2. Емкостное сопротивление конденсатора
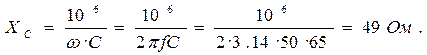
3. Токи в ветвях


4. Коэффициенты мощности ветвей
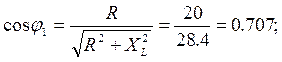
 (отстающий)
(отстающий)
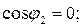
 (опережающий).
(опережающий).
5. Активные и реактивные составляющие токов ветвей

 ;
;
I R2=0; I P2=2.04·1.0=2.04 A.
6. Ток в неразвлетвленной части цепи

Реактивные токи ветвей должны вычитаться, так как реактивный ток ветви с емкостью принимается отрицательным.
7. Коэффициент мощности всей цепи
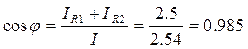
8. Активные мощности ветвей
 P 2=0
P 2=0
Построение векторной диаграммы начинаем c вектора напряжения U (рис. 4). Под углом φ 1 к вектору напряжения (в сторону отставания) откладываем вектор тока I 1, под углом φ 2 (в сторону опережения) - вектор тока I 2. Геометрическая сумма этих векторов представляет ток I в неразветвленной части цепи. Проекции токов ветвей на вектор напряжения являются активными составляющими I R1 и I R2; проекции этих токов на вектор, перпендикулярный вектору напряжения, - реактивными составляющими I P1 и I P2.
9. При резонансе токов ток I совпадает на фазе с напряжением, что возможно при равенстве реактивных токов ветвей I P1= I P2 (см. векторную диаграмму (рис.5)).
Тогда емкостное сопротивление этой ветви

отсюда

|
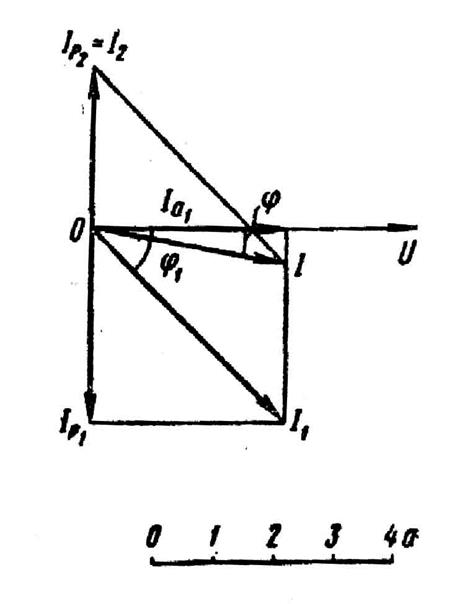
Рис. 5.