Пример решения задачи на расчет трехфазной цепи соединенной звездой.

Puc. 6.

Задача: В каждую фазу трехфазной четырехпроводной сети включили сопротивления так, как показано на рис. 6. Величины сопротивлений даны на рисунке. Линейное напряжение сети U =380 B. Определить: линейные токи, углы сдвига фаз, ток в нулевом проводе, активную, реактивную и полную мощности трех фаз. Построить в масштабе векторную диаграмму.

Решение. 1. Полные сопротивления фаз:

2. Углы сдвига фаз:

(опережающий);

(отстающий);

.

3. Фазное напряжение

4. Линейные (фазные) токи:

5. Активная мощность потребляется только активными сопротив­лениями. Поэтому активная мощность трех фаз

6. Реактивная мощность потребляется только реактивными сопро­тивлениями. Поэтому реактивная мощность трех фаз

Знак «минус» показывает, что реактивная мощность системы но­сит емкостный характер.

7. Полная мощность трех фаз:

8. Построение векторной диаграммы начинаем с векторов фаз­ных напряжений.

Рис. 7.

Из точки О (рис. 7) в принятом масштабе напряжений прово­дим три вектора фазных напряжений , и , углы между которыми составляют 120°. Затем строим векторы линейных напря­жений , и 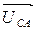, согласно уравнениям:

= - = +(- );

= - = +(- );

= - = +(- )

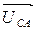Черточки над буквами показывают, что векторы должны вычи­таться и складываться геометрически. Например, для построения линейного напряжения к вектору нужно геометрически прибавить обратный по направлению вектор .

Под углом φ _А=53° в сторону опережения вектора фазного на­пряжения откладываем в принятом масштабе токов вектор то­ка ; под углом φ _В=37° в сторону отставания от вектора фазного напряжения откладываем вектор тока .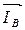

Вектор тока совпадает по направлению с вектором фазного напряжения так как φ _С=0.

Для определения тока в_нулевом проводе I ₀ складываем геомет­рически векторы токов , и . Из векторной диаграммы, поль­зуясь масштабом для токов, нахо­дим ток I ₀=34 A.

Пример 2: В каждую фазу трехфазной сети включили сопро­тивления так, как показано на рис. 8. Величины сопротивлений даны на рисунке3. Линейное напря­жение сети U =220 B.

Рис. 8.

Определить: фазные и линей­ные токи, углы сдвига фаз, актив­ную, реактивную и полную мощ­ности трех фаз. Построить в мас­штабе векторную диаграмму.

Решение 1. Полные со­противления фаз:

2. Углы сдвига фаз:

(отстающий);

(опережающий).

3. Фазные токи:

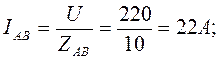
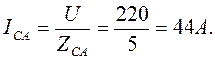
4. Активная мощность потребляется только активными сопро­тивлениями. Поэтому активная мощность трех фаз

5. Реактивная мощность потребляется только реактивными со­противлениями. Поэтому реактивная мощность трех фаз

6. Полная мощность трех фаз

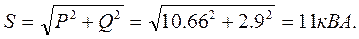
7. Для определения линейных токов строим векторную диаграм­му (рис. 4). Построение _начинаем с векторов фазных (линейных) напряжений , и .

Вектор тока совпадает с вектором фазного напряжения , так как φ _АВ=0.

Вектор тока отстает от вектора на угол φ _ВС =90°, а вектор тока опережает вектор на угол φ _ВС =53°.

Линейные ток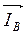и , и на диаграмме равны геометрической разности соответствующих фазных токов. Например, , т.е. ток в линейном проводе А равен геометрической сумме вектора фазного тока и обратного вектора фазного тока .

Из векторной диаграммы графически, пользуясь масштабом, определяем линейные токи: I _A=66 A; I _B=43 A; I _C=25 A.