Задана функциональная схема потенциометрической следящей системы автоматического управления (САУ), рис.1.

Рис. 1 Функциональная схема следящей системы
В схему входят следующие элементы: КУ- корректирующее устройство, МУ – магнитный усилитель, Д- двигатель постоянного тока, приводящий в движение исполнительный механизм. Математическая модель данной структуры представлена в виде структурной схемы, рис.2. Значения коэффициентов передачи и постоянных времени звеньев приведены в табл.2.

Рис.2. Структурная схема системы
Необходимо:
1. Определить передаточную функцию разомкнутой системы.
2. Найти передаточную функцию замкнутой системы при единичной отрицательной обратной связи.
3. Определить предельное значение коэффициента передачи по условию устойчивости системы. Таблица 2
| Параметр | Вариант | |||||||||

| 5,0 | 1,43 | 1,5 | 4,17 | 6,34 | 4,44 | 5,0 | 2,22 | 3,33 | 2,0 |

| 2,5 | 3,0 | 4,0 | 1,5 | 2,0 | 0,8 | 3,0 | 6,5 | 1,5 | |

| 0,2 | 0,3 | 0,4 | 0,2 | 0,06 | 0,07 | 0,05 | 0,1 | 0,1 | 0,25 |

| 2,0 | 1,5 | 2,0 | 3,5 | 2,0 | 0,5 | 2,5 | 2,5 | ||

| 1,2 | 5,0 | 3,2 | 2,0 | 2,0 | 2,0 | 3,0 | 4,0 | 3,0 | 2,0 |

| 0,5 | 0,4 | 0,3 | 0,3 | 0,3 | 0,2 | 0,15 | 0,3 | 0,2 | 0,5 |
| Параметр | Вариант | |||||||||

| 3,0 | 1,3 | 2,5 | 5, 7 | 7,1 | 4,4 | 6,0 | 2,4 | 3,4 | 8,0 |

| 3,5 | 3,6 | 4,2 | 1,3 | 2,1 | 0,48 | 3,1 | 3,5 | 2,5 | |

| 0,12 | 0,23 | 0,2 | 0,05 | 0,09 | 0,17 | 0,07 | 0,15 | 0,6 | 0,4 |

| 3,7 | 2,7 | 1,8 | 2,5 | 3,2 | 3,6 | 2,2 | 0,59 | 3,5 | 1,5 |

| 1,5 | 5,7 | 3,7 | 2,1 | 2,8 | 1,9 | 3,4 | 4,25 | 5,6 | 3,0 |

| 0,5 | 0,3 | 0,25 | 0,36 | 0,3 | 0,5 | 0,18 | 0,32 | 0,27 | 4,5 |
Методические указания
Если на структурной схеме, рис.2, удалить цепь отрицательной обратной связи, то схема станет разомкнутой и приобретёт вид, рис. 3.
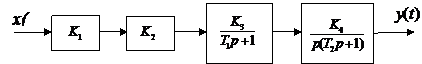
Рис.3. Структурная схема разомкнутой САУ
Система состоит из четырех последовательно включённых звеньев. Общая передаточная функция в этом случае определяется как
|
|
W раз(p) =W 1(p) W 2(p) W 3(p) W 4(p),
Тогда схема рис.3 может быть представлена в виде рис. 4 а. где К=К 1 К 2 К 3 К 4 – общий коэффициент усиления
 |  | ||
а) б)
Рис.4. Структурные схемы САУ: а – разомкнутая; б - замкнутая
Если разомкнутую схему рис.4а охватить единичной обратной связью то она примет вид рис. 4б. Её общую передаточную функцию можно определить по формуле

В результате схему рис. 4б можно свернуть и представить в виде рис.5
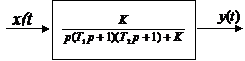 |
Рис.5. Структурная схема САУ в свернутом виде
Устойчивость САУ определяется по характеристическому уравнению, полином которого находится в знаменателе передаточной функции замкнутой системы. Воспользуемся критерием устойчивости Гурвица, который формируется следующим образом: система будет устойчивой, если при аi>0 главный определитель Гурвица Δ и все его диагональные миноры Δ i будут больше нуля.
Характеристическое уравнение системы

После преобразований получим

Обозначим коэффициенты при p соответственно 
Тогда это уравнение будет иметь вид
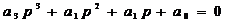
где 
Условие устойчивости системы по критерию Гурвица для уравнения третьего порядка определяется:

Для решаемой задачи это означает 
Подставляя в это неравенство коэффициенты а i, получаем:  или
или 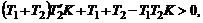
Отсюда условие устойчивости

и величина предельного коэффициента передачи

Литература
- Дронов В.В. Основы теории управления. Конспект лекций–В. Новгород, 2010
2. Теория автоматического управления: Учеб. для вузов/ С.Е. Душин, Н.С. Зотов, Д.Х. Имаев и др.; Под ред. В. Б. Яковлева.- М.: Высшая школа, 2009.– 567 с.
|
|
- Шандров Б. В. Технические средства автоматизации: учебник для студeнтов высших учебных заведений.- М.: Издательский центр «Академия», 2007. — 368 с.
Певзнер Л.Д. Практикум по теории автоматического управленияю. –М.:Высш. школа,2006.–590 с.
- Теория систем автоматического управления Бесекерский В.А., Попов Е.П.– СПб.: Профессия, 2007.–761 с.