Практическая работа №2.
Тема: «Нахождение производной функции»
Цель: Сформирование практические навыки нахождения производных функций;
Теоретическая часть
Производной функции 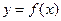 в точке
в точке 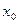 называется предел отношения приращения
называется предел отношения приращения 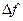 функции в этой точке к приращению
функции в этой точке к приращению 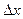 аргумента, когда приращение аргумента стремится к нулю:
аргумента, когда приращение аргумента стремится к нулю:
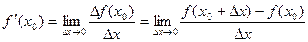 .
.
Функция 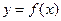 , имеющая производную в каждой точке некоторого промежутка, называется дифференцируемой в этом промежутке.
, имеющая производную в каждой точке некоторого промежутка, называется дифференцируемой в этом промежутке.
Производная функции 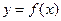 обозначается
обозначается 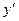 ,
, 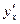 ,
, 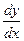 или
или 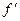 ,
, 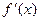 ,
, 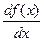 .
.
Нахождение производной называется дифференцированием.
Правила дифференцирования
1. 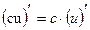 , c – const,
, c – const,
2. 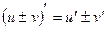
3. 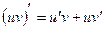 , где
, где 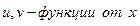
4. 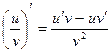
Таблица производных элементарных функций
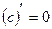 , c - const , c - const
| 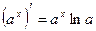
|
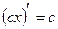
| 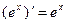
|
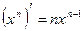
| 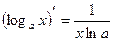
|
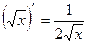
| 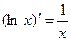
|
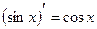
| 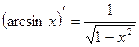
|
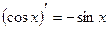
| 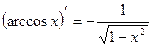
|
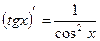
| 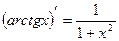
|
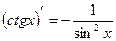
| 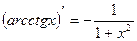
|
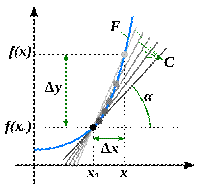
Геометрический смысл производной
Производная функции 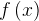 в точке
в точке 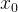 равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.
равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.
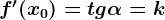
Пример 1. На рисунке изображён график функции 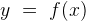 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой 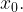 Найдите значение производной функции
Найдите значение производной функции 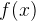 в точке
в точке 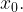
Производная функции 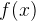 в точке
в точке 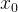 равна тангенсу угла наклона касательной, проведенной в точке
равна тангенсу угла наклона касательной, проведенной в точке 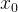 .
.
Достроив до прямоугольного треугольника АВС, получим:
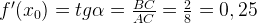
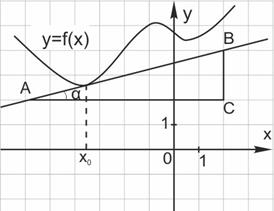
Ответ: 0,25.
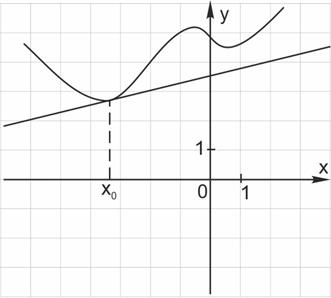
Пример 2. На рисунке изображён график функции 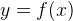 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой 
Найдите значение производной функции 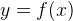 в точке
в точке 

Начнём с определения знака производной. Мы видим, что в точке 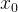 функция убывает, следовательно, её производная отрицательна. Касательная в точке
функция убывает, следовательно, её производная отрицательна. Касательная в точке 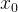 образует тупой угол
образует тупой угол 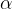 с положительным направлением оси
с положительным направлением оси 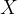 . Поэтому из прямоугольного треугольника мы найдём тангенс угла
. Поэтому из прямоугольного треугольника мы найдём тангенс угла 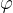 , смежного с углом
, смежного с углом 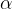 .
.
Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: 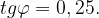 Поскольку
Поскольку 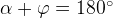 , имеем:
, имеем:
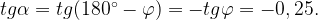
Ответ: −0, 25.
Касательная к графику функции
Пример 3. Прямая 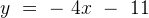 является касательной к графику функции
является касательной к графику функции 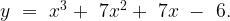
Найдите абсциссу точки касания.
Запишем условие касания функции 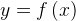 и прямой
и прямой 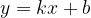 в точке
в точке 
При 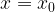 значения выражений
значения выражений  и
и 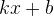 равны.
равны.
При этом производная функции  равна угловому коэффициенту касательной, то есть
равна угловому коэффициенту касательной, то есть 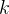 .
.
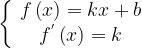
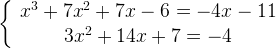
Из второго уравнения находим 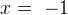 или
или 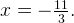 Первому уравнению удовлетворяет только
Первому уравнению удовлетворяет только 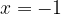 .
.
Физический смысл производной
Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике. Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.
Пример 1. Материальная точка движется прямолинейно по закону 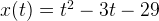 , где
, где 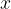 — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, 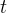 — время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени
— время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени 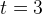 с.
с.
Мгновенная скорость движущегося тела является производной от его координаты по времени. Это физический смысл производной. В условии дан закон изменения координаты материальной точки, то есть расстояния от точки отсчета: 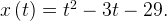
Найдем скорость материальной точки как производную от координаты по времени:
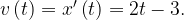 В момент времени
В момент времени 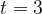 получим:
получим:
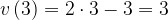 .
.
Ответ: 3
| ХОД РАБОТЫ Внимательно изучите теоретическую часть практической работы, основные и дополнительные источники и дайте развёрнутые ответы на контрольные вопросы: 1. Дайте определение производной функции, какая функция называется дифференцируемой, что означает дифференцирование функции. 2. Какие вы знаете правила дифференцирования. 3. Составьте таблицу производных. 4. В чём состоит геометрический смысл производной, приведите примеры. 5. В чём состоит физический смысл производной, приведите примеры. |
Основные источники:
1. Григорьев С.Г., Иволгина С.В. «Математика»: учебник для студ. образоват. учреждений сред.проф. образования под редакцией В.А. Гусева. – 10-е изд., стер. – М.: Издательский центр «Академия», 2018.
Дополнительные источники:
2. Богомолов Н.В., Самойленко П.И. «Математика» учебник для средних спец. учебных заведений -5 изд., переработанное и доп. – М.: издательство Юрайт, 2015.
3. Богомолов Н.В. практические занятия по математике: учебное пособие для СПО / Н.В. Богомолов. – 11-е изд., перераб. И доп. –М.: издательство Юрайт, 2015.
4. Федеральное хранилище Единой коллекции цифровых образовательных ресурсов [Электронный ресурс] / Национальный фонд подготовки кадров – Электрон.дан. – Режим доступа: https://school-collection.edu.ru/catalog/– Загл. с экрана;
5. Единое окно доступа к образовательным ресурсам [Электронный ресурс]: каталог образовательных Интернет - ресурсов/ ФГУ ГНИИ ИТТ «Информика». – Электрон.дан. – Режим доступа: https://window.edu.ru/– Загл. с экрана