Как уже отмечалось, излишнее увеличение материальных запасов предприятиям экономически невыгодно. При этом базовая модель Уилсона предполагает независимость цены приобретения (С) товара от объема закупки. Однако реальным хозяйствующим субъектам поставщики могут предоставлять скидки в зависимости от размера приобретаемой партии. В этом случае перед финансовыми менеджерами предприятия стоит вопрос о выяснении такого размера скидок, которые за отчетный период компенсируют повышенные расходы на хранение приобретаемой продукции.
В этом случае в общую модель суммарных издержек (1) необходимо добавить фактически понесенные затраты Спр на приобретение товара:
CΣ = Cc + Co + Спр = I*Q/2 + F*D/Q + С*D, (5)
Пример.
Рассмотрим теперь деятельность того же магазина при условии, что упомянутые пакетики поставщик готов отгружать по цене 1,9 руб., если размер приобретаемой партии составляет 200 шт.
Решение.
Как видно из предыдущих вычислений, нам предлагают увеличить объем закупки с 158 до 200 шт. Мы пытаемся установить для себя выгодность этого условия. При этом полагаем, что при новой цене С1 < C суммарная величина понесенных затрат равна (5)
СΣ = 0.4*158/2 + 10*500/158 + 2*500 =1063,25 руб. – для С = 2 руб.
и
СΣ = 0.38*200/2 + 10*500/200 + 1,9*500 = 1013 руб. – для С1 = 1,9 руб.
Анализируя полученные значения приходим к выводу, что предложение поставщика следует принять.
1.3. Модель планирования экономического размера партии
Основную модель, используемую для моделирования процессов приобретения запасов у внешнего поставщика можно распространить и на другие производственные ситуации, большинство из которых предполагает частичное восполнение запасов за счет их производства на данном предприятии.

Рис.2. Изменение уровня запасов при наличии собственного производства
В этом случае исходное допущение модели Уилсона о мгновенном изменении уровня запасов от 0 до Q не может быть принято. Это изменение в действительности характеризуется некоторым временным интервалом t в течение которого происходит увеличение запасов (рис.2). В этом случае принято говорить о модели с продолженной поставкой, и в качестве параметра оптимизации здесь выступает оптимальный размер партии запасов, произведенной своими силами. За это же время (t) происходит одновременное потребление произведенного ресурса.
Очевидно, что в этом случае восполнение запасов происходит в количестве H (H < Q), причем средний уровень запасов на предприятии равен H/2. Если обозначить через λ интенсивность производства (шт./ед.вр.) и через γ – интенсивность потребления (шт./ед.вр.), то
H = t*(λ - γ), где t=Q/λ,
откуда средний запас равен
 , (6)
, (6)
и при известном числе партий (т.е. тех же самых заказов на поставку, только не от сторонних поставщиков)
n = γ/Q
суммарные затраты производства СΣ можно представить в виде:
СΣ = I*H/2 + F*n  + F*γ /Q, (7)
+ F*γ /Q, (7)
откуда
Q* =  (8)
(8)
Пример.
Если предположить, что в рассмотренном нами магазине существует производственный процесс, при котором на станке производится партия бумажных пакетиков в количестве 10 пакетиков в день. По оценкам специалистов стоимость производства одного пакетика равна 2,5 руб., издержки хранения оцениваются как 20 % цены изделия, годовые затраты на подготовку технологического процесса их производства составляют 500 руб. Необходимо определить оптимальный размер партии пакетиков и частоту запуска производства этих партий.
Решение.
В данном случае плановый период равен 1 году. Стоимость подготовки производственного процесса аналогична издержкам на размещение заказа у сторонних поставщиков F = 500 руб. Интенсивность потребления γ = 500 пакетов/год, интенсивность производства λ = 3000 шт./год, I = i*C = 0.2*2.5 = 0.5 руб./год за пакетик.
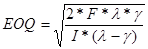 =
=  = 1095 пакетиков.
= 1095 пакетиков.
В год таких партий потребуется 500/1095 = 0,46 партии, т. е. запуск производства необходимо осуществлять приблизительно 1 раз в 2 года. При этом время работы станка составит 1095/10 = 109,5 дней, а суммарные годовые затраты по управлению запасами составляют по ф-ле (7):
СΣ  +
+  = 456,44 руб.
= 456,44 руб.