Выполним расчет сосуда, состоящего из участков сферической, цилиндрической и конической оболочек (рис.10), по безмоментной теории.
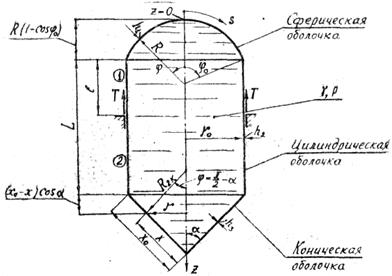
Рис.10. Расчетная схема сосуда
Геометрические размеры сосуда  известны. Заданы также модуль упругости Е и коэффициент Пуассона m материала сосуда. Сосуд заполнен жидкостью с плотностью r. Жидкость находится под давлением p.
известны. Заданы также модуль упругости Е и коэффициент Пуассона m материала сосуда. Сосуд заполнен жидкостью с плотностью r. Жидкость находится под давлением p.
Если пренебречь весом сосуда, то реакция кольцевой опоры будет численно равна весу жидкости, заключенной в сосуде:
 (9)
(9)
где g = r g – удельный вес жидкости, V - объём сосуда.
Расчет сосуда производим по отдельным его элементам.
Сферическая оболочка
Сферическая оболочка нагружена давлением
 (10)
(10)
переменным вдоль дуги меридиана.
Главные радиусы кривизны сферической оболочки:
R 1 = R 2= R (11)
радиус параллельного круга
r = R sin j (12)
Нормальным коническим сечением с углом 2φ при вершине выделим часть сферической оболочки, как показано на рис. 11.

Рис.11. Расчетная схема сферической оболочки
Уравнение равновесия отсеченной части оболочки:
 (13)
(13)
Осевую равнодействующую P z сф внешней нагрузки q = var на рассматриваемую часть оболочки находим по выражению (5), переходя к интегрированию по переменной j:
 (14)
(14)
Подставляя полученное выражение для P z сф в уравнение (13) находим меридиональные напряжения в оболочке
 . (15)
. (15)
Подставляя значения главных радиусов кривизны (11) и выражение (10) для давления q в уравнение Лапласа (3), получаем следующее соотношение:
 (16)
(16)
откуда c помощью выражения (15) находим кольцевые напряжения в оболочке:
 . (17)
. (17)
Радиальные перемещения точек оболочки определяем по формуле (7) с использованием выражений (15) и (17)
 (18)
(18)
Формулу для определения углов поворота нормали к оболочке получим, подставляя соотношение (16) в выражение (8):
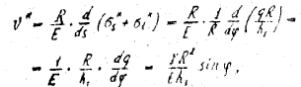 (19)
(19)
Коническая оболочка
Главные радиусы кривизны конической оболочки:
 (20)
(20)

Рис.12. Расчетная схема конической оболочки.
При расчете конической оболочки удобно ввести параметр x, определяющий расстояние исследуемого сечения от вершины конуса по образующей (см. рис. 10). Радиус параллельного круга и второй главный радиус кривизны конической оболочки выражаются через параметр х очевидными соотношениями:
 (21)
(21)
Внешняя нагрузка изменяется вдоль образующей конуса по закону:
 (22)
(22)
Кольцевые напряжения в оболочке находим из уравнения Лапласа:
 (23)
(23)
Меридиональные напряжения находим из уравнения равновесия зоны оболочки, отсеченной нормальным коническим сечением c углом 2 j при вершине, (рис.12):
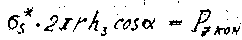 (24)
(24)
Осевую равнодействующую P z кон внешней нагрузки на отсеченную часть оболочки, ограниченную параллельным кругом r = x sin a (рис. 12)., находим по выражению (5), переходя к интегрированию по переменной х и принимая во внимание, что cos j = sin a:
 (25)
(25)
Подставляя полученное выражение в уравнение (24) находим меридиональные напряжения в оболочке:
 (26)
(26)
Радиальные перемещения точек оболочки находим по формуле (7):
 (27)
(27)
где ss и st определены выражениями (23) и (26).
Угол поворота нормали к оболочке определяем по формуле (8), используя выражения (23) и (26):
 (28)
(28)
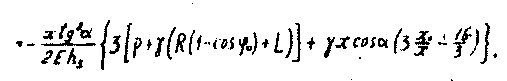 (28)
(28)
Цилиндрическая оболочка
Цилиндрическая оболочка нагружена переменным давлением
 (29)
(29)
Координата z изменяется в пределах
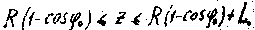
Главные радиусы кривизны цилиндрической оболочки
 (30)
(30)
Радиус параллельного круга
r = r 0 (31)
При определении меридиональных напряжений следует учесть, что цилиндрическая оболочка имеет в данном случае два участка нагружения (см.рис.10):
1 участок - от сферической крышки до кольцевой опоры

2 участок - от кольцевой опоры до конического днища
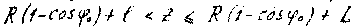
Расчетная схема для 1 участка цилиндрической оболочки представлена на рис.13.

Рис.13. Расчетная схема цилиндрической оболочки (1 участок)
Уравнение равновесия рассматриваемой части сосуда:
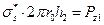 (32)
(32)
Осевую равнодействующую сил давления среда на сферическую крышку сосуда можно определить из выражения (14) полагая в нем j = j 0
 (33)
(33)
Расчетная схема для 2 участка цилиндрической оболочки представлена на рис.14

Ряо.14. Расчетная схема цилиндрической оболочки (2 участок).
Уравнение равновесия рассматриваемой части сосуда:
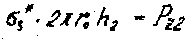 (34)
(34)
где P z2- осевая равнодействующая сил давления среды на коническое днище сосуда. Величину ее можно определить из выражения (25), полагая в нем x = x 0:
 (35)
(35)
В результате получаем следующие формулы для определения меридиональных напряжений в цилиндрической оболочке:
- на 1 участке
 (36)
(36)
на 2 участке
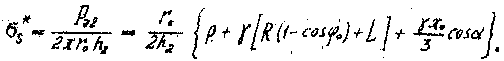 (37)
(37)
Кольцевые напряжения в оболочке находим, подставляя значения главных радиусов кривизны (30 в выражение (29) для давления q в уравнение Лапласа (3). В результате получим следующую формулу:
 , (38)
, (38)
общую для 1 и 2 участков оболочки.
Радиальные перемещения точек цилиндрической оболочки определяем по формуле (7):
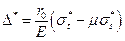
Таким образом,
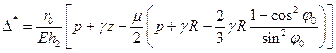 на первом участке,
на первом участке,
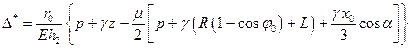 на втором участке. (39)
на втором участке. (39)
Угол поворота нормали к оболочке определяем по формуле (8):
 (40)
(40)
Численный расчет выполним для следующих значений параметров сосуда и нагрузки:
r 0 = 500 мм, j 0 = 60°, p = 0,1 МПа,
L = 7000 мм, a = 45°, r = 1,02 кг/м3,
l = 3500 мм, E = 2×105 МПа, m = 0,3
h 1 = h 2 = h 3 = 10 мм.
Очевидно, что
 ,
,
 ,
,
g = r × g = 10-5 Н/мм3.
Подставляя значения параметров в выражения для напряжений и перемещений, получаем следующие расчетные формулы для элементов сосуда:
– для сферической оболочки:
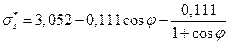 , (41)
, (41)
 , (42)
, (42)
 , (43)
, (43)
 . (44)
. (44)
– для цилиндрической оболочки:
 на первом участке,
на первом участке,
 на втором участке; (45)
на втором участке; (45)
 , (46)
, (46)
 на первом участке,
на первом участке,
 на втором участке; (47)
на втором участке; (47)
 ; (48)
; (48)
– для конической оболочки:
 , (49)
, (49)
 , (50)
, (50)
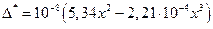 , (51)
, (51)
 . (52)
. (52)
Результаты расчета сводим в табл. 1
Таблица 1
Результаты расчета сосуда по безмоментной теории
| Элемент сосуда | Координата точки | Расчетные величины | ||||
| ss*, МПа | st*, МПа | D*×103, мм | u*×106, рад | |||
| Сферическая оболочка | j | |||||
| 2,96 | 0,83 | |||||
| 5,35 | 1,44 | |||||
| Цилиндрическая оболочка | z, мм | 11,0 | 1,25 | |||
| 3789 -0 | 15,3 | 1,25 | ||||
| 3789 +0 | 14,0 | 1,25 | ||||
| 18,3 | 1,25 | |||||
| Коническая оболочка | x, мм | 25,9 | -89,4 | |||
| 6,45 | -45,4 | |||||
По результатам расчета строим эпюры меридиональных и кольцевых напряжений, радиальных и угловых перемещений для элементов сосуда, руководствуясь при этом известными из курса математического анализа правилами построения графиков кривых по их уравнениям.
На рис.15 показано распределение меридиональных и кольцевых напряжений в элементах сосуда. На рис.16 представлены эпюры радиальных и угловых перемещений.
Анализ полученных результатов приводит нас к выводу, что безмоментная теория не дает удовлетворительного решения задачи о расчете сосудов, состоящих из оболочек различной геометрической формы. Этот вывод следует из того, что в точках сопряжения элементов сосуда расчет по безмоментной теории дает нам скачки величин радиальных и угловых перемещений, 45а это противоречит условию неразрывности конструкции.

Рис.15. Графики меридиональных и кольцевых напряжений
в элементах сосуда
Полученные результаты справедливы для участков сосуда, находящихся на некотором удалении от точек сопряжения. В узких зонах элементов сосуда, примыкающих к точкам сопряжения, а также к кольцевой опоре, возникает моментное напряженное состояние, которое носит название краевого эффекта. Исследование напряженно-деформированного состояния в зонах краевого эффекта необходимо выполнять методами моментной теории оболочек.
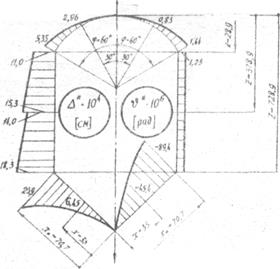
Рис.16. Графики радиальных и угловых перемещений элементов сосуда
Необходимо отметить, что вершина конической оболочки является особой точкой (в окрестности вершины, в частности, -нарушается условие тонкостенности оболочки), и исследование напряженно-деформированного состояния зона оболочки, примыкающей к вершине, следует проводить особыми методами.