ЭЛЕМЕНТАРНЫЕ СВЕДЕНИЯ ПО ГЕОМЕТРИИ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНЖЕНЕРНОЙ ЭКОЛОГИИ

Кафедра «Системы автоматизированного проектирования»

 

 

 

РАСЧЕТ ТОНКОСТЕННЫХ КОНСТРУКЦИЙ

ОБОЛОЧЕЧНОГО ТИПА

Часть 1

 

(методические указания)

 

 

Москва – 2002

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Курс "Методы и алгоритмы расчетов на прочность в САПР" изучается студентами специальности 220300 в течение 5 и 6 семестров. Теория тонкостенных оболочек враще­ния является одним из разделов этого курса и изучается в 5 семестре. В процессе изучения этого раздела студенты выпол­няют расчетно-проектировочную работу по расчету сосудов. Настоящая методическая разработка составлена применительно к выполнению этой работы. Теория и основы расчета оболочек вращения излагаются на лекциях и практических занятиях по курсу в достаточно полном объёме. Поэтому здесь мы ограничиваемся сводкой основных понятий теории оболочек, краткими указани­ями и пояснениями отдельных вопросов и основное внимание сосредотачиваем на решении конкретных задач.

При изучении основ расчета тонкостенных оболочек враще­ния студент должен обратить внимание на следующие вопросы:

1. Обычно оболочку относят к тонким при , где

Эта оценка условная, ориентировочная и зависит от степени погрешности расчета, принятой в качестве допустимой. Оболочку с большей величиной отношения тоже можно рассматривать как тонкостенную, но при этом следует иметь в виду, что погрешность расчета возрастает вместе с величиной этого отношения. На практике теорию тонких оболо­чек иногда применяют и при величинах отношения .

 

2. Необходимо тщательно проработать постановку задачи о расчете оболочек, уяснить при этом физический смысл принятых допущений. При изучении условий возникновения в оболочке безмоментного напряженного состояния обратите внимание на условия закрепления края оболочки.

3. Обратите внимание на размерности внутренних усилий в оболочке и внешних моментной и радиальной нагрузок. Все эти усилия равномерно распределены но окружности. Рассматриваются их величины, приходящиеся на единицу длины окружности.

4 Студент должен хорошо усвоить правило знаков для радиальных и угловых перемещений. Радиальное перемещение счи­тается положительным, если сопровождается увеличением радиуса параллельного круга. Угол поворота нормали к срединной поверхности оболочки будем считать положительным, если нормаль поворачивается как показано на рис.9.

5. Основная трудность при расчете оболочек по безмоментной теории заключается в правильной записи уравнения равнове­сия зоны оболочки, в частности, в определении осевой равно­
действующей внешней нагрузки. При составлении уравнения равновесия зоны силы взаимодействия между оболочкой и средой могут рассматриваться как внешние по отношению к оболочке. В этом случае записывается уравнение равновесия собственно оболочки, и осевая равнодействующая внешней нагрузки определяется ин­тегралом (5), стр.14.

Можно также рассматривать равновесие оболочки вместе с содержащейся в ней жидкостью. Силы взаимодействия между обо­лочкой и жидкостью в этом случае являются внутренними и в уравнение равновесия не входят.

Студент должен хорошо усвоить, по крайней мере, один из этих способов составления уравнения равновесия зоны. Для этого необходимо внимательно рассмотреть решение задачи, выполненное в п.п. 6 и 7 настоящего пособия.

При выполнении расчетно-проектировочной работы допуска­ется определять численные значения напряжений и перемещений только на границах элементов сосуда. При построении графиков точки, соответствующие найденным значениям, соединяются кри­выми, характер которых определяется по их уравнениям.

В 1 части настоящего пособия основное внимание уделяется расчету оболочек по безмоментной теории. Вторая часть посвя­щена расчету сопряжений оболочек различной геометрической формы методами моментной теории. В приложении к разработке приведены формулы для расчета длинных цилиндрических, кони­ческих и сферических оболочек.

 

ОБОЗНАЧЕНИЯ

 

R ₁, R ₂ – главные радиусы кривизны, мм;

r – радиус параллельного круга, мм;

h – толщина оболочки, мм;

m – моментная нагрузка, равномерно распределенная по окружности, Н*мм/мм;

P – радиальная нагрузка, равномерно распределенная по окружности, Н/мм;

q – распределенная по площади нагрузка, МПа;

N _s – нормальное меридиональное усилие, Н/мм;

N _t – нормальное кольцевое усилие, Н/мм;

M _s – меридиональный изгибающий момент, Н*мм/мм;

M _t – кольцевой изгибающий момент, Н*мм/мм;

Q – поперечное усилие, Н/мм;

s _s – нормальное меридиональное напряжение, МПа;

s _t – кольцевое меридиональное напряжение, МПа;

D – радиальное перемещение, мм;

u – угол поворота нормали к срединной поверхности оболочки, рад;

s _s^*, s _t^* – нормальные меридиональные и кольцевые напряжения, вычисленные по безмоментной теории, МПа;

D ^*, u ^* – радиальное и угловое перемещения, вычисленные по безмоментной теории;

P _z – осевая равнодействующая внешней нагрузки на оболочку, Н;

E – модуль упругости материала оболочки, МПа;

m – коэффициент Пуассона материала оболочки.

 

 

СОДЕРЖАНИЕ

 

1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ …………………………………………………… 5

2. ЭЛЕМЕНТАРНЫЕ СВЕДЕНИЯ ПО ГЕОМЕТРИИ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ ………..5

3. ОСНОВЫТЕОРИИ ТОНКОСТЕННЫХ ОБОЛОЧЕК ВРАЩЕНИЯ. ПОСТАНОВКА ЗАДАЧИ …………………………………………………………………………………………… 6

4. ВНУТРЕННИЕ УСИЛИЯ И НАПРЯЖЕНИЯ В ОБОЛОЧКЕ …………………………………..7

5. РАСЧЕТ ОБОЛОЧЕК ВРАЩЕНИЯ ПО БЕЗМОМЕНТНОЙ ТЕОРИИ ………………………..8

6. ПРИМЕР РАСЧЕТА СОСУДА ПО БЕЗМОМЕНТНОЙ ТЕОРИИ ………………………….....11

6.1. Сферическая оболочка ……………………………………………………………………… 11

6.2. Коническая оболочка ……………………………………………………………………….. 13

6.3. Цилиндрическая оболочка …………………………………………………………………..15

7. К ВОПРОСУ О РАСЧЕТЕ МЕРИДИОНАЛЬНЫХ НАПРЯЖЕНИЙ ………………………..19
1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

 

Под оболочкой понимается тело, одно из измерений которого – толщина – значительно меньше двух других. Геометриче­ское место точек, равноотстоящих от обеих поверхностей оболочки, носит название срединной поверхности. Осесимметричными или просто симметричными оболочками (оболочками вращения.) называются такие, срединная поверхность которых представляет собой поверхность вращения (рис.1).

 

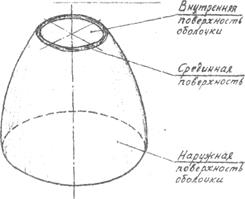
Рис 1. Тонкостенная оболочка вращения

 

В дальнейшем будем рассматривать осесимметричные оболочки постоянной толщины, малой по сравнению с размерами оболочки. Полагаем при этом, что нагрузка, действующая на оболочку, также осесимметрична. Для таких оболочек задача рас­чета значительно упрощается вследствие того, что возникающие в оболочке внутренние усилия и перемещения изменяются только вдоль образующей, оставаясь неизменными в окружном направления.

 

ЭЛЕМЕНТАРНЫЕ СВЕДЕНИЯ ПО ГЕОМЕТРИИ

ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ

Плоская кривая, вращением которой вокруг некоторой оси образована поверхность, называется образующей, точки пересечения ее с осью вращения – полюсами. Кривая, образованная на поверхности сечением ее плоскостью, проходящей через ось, называется меридианом. Очевидно, меридианы совпадают с образующими. Плоскости, перпендикулярные оси вращения, пересекают поверхность по окружностям, называемым параллельными кругами.

Проведем нормаль n – n к поверхности в некоторой ее точ­ке Р (рис.2). Связка плоскостей, проходящих через нормаль, пересекает поверхность по линиям, называемым нормальными сечениями. Радиусы кривизны этих сечений в точке Р будут в общем случае различны.

Рис.2. Поверхность вращения

Очевидно, меридиан поверхности также является нормальным сечением. Меридиан и нормальное сечение поверхности плоскостью, перпендикулярной меридиану (перпен­дикулярной касательной к меридиану в точке Р), отличаются тем, что из всех нормальных сечений в данной точке они имеют наибольший и наименьший радиусы кривизны.

Радиус кривизны меридиана называется первым главным ра­диусом кривизны R ₁ поверхности в данной точке (отрезок нормали К ₁ Р на рис.2), радиус кривизны нормального сечения плос­костью, перпендикулярной меридиану, – вторым главным радиусом кривизны R ₂ поверхности в этой точке (отрезок нормали К ₂ Р между точкой Р и осью вращения поверхности на рис.2. Центры кривизны К ₁ и К ₂ лежат на нормали к поверхности в этой точке, причем второй центр кривизны К ₂ поверхности вращения лежит на оси вращения, как это доказывается в дифференциальной геометрии.

Нормали, проведенные к поверхности в точках параллель­ного крута, пересекаются в одной точке, лежащей на оси вра­щения, и образуют коническую поверхность, нормальную к рас­сматриваемой поверхности.

Радиус параллельного круга r связан со вторым главным радиусом кривизны очевидным соотношением:

, (1)

где ( - угол между нормалью к поверхности и осью вращения).

Теперь можно дать более точное определение понятию тонкой оболочки. Тонкостенными считаются оболочки, для которых выполняется соотношение 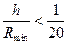, где h - толщина оболочки, R _min = min(R ₁, R ₂).

В теории оболочек доказывается, что относительная погрешность расчета не превышает величины . Поэтому, при­нимая указанное выше соотношение, мы обеспечиваем обычную для технических задач точность расчета.

В зависимости от формы срединной поверхности различают оболочки цилиндрические, конические, сферические и. т.д.