Момент силы
Перейдем к динамике вращения.
Желательно изобрести аналог силы - момент силы. Это причина, которая заставляет тело вращаться. Для того, чтобы выразить момент силы количественно, можно приравнять работу, которая производится при повороте тела на какой-то угол, к произведению момента силы на этот угол.
Пусть сила F приложена к точке (x, y).
D А = Fx D x + Fy D y
Учитывая, что D x = - y Dq; D y = x Dq
D А = (xFy - yFx) Dq
Моментом силы N является «странная» комбинация сил и расстояний
N = xFy - yFx.
Если на тело действует несколько сил, то моменты их складываются при определении работы: Ni = xiFyi - yiFxi;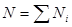 
Для того, чтобы тело не вращалось нужно, чтобы суммарный момент N = 0 относительно какой-то одной произвольной оси (двумерный случай).
Выясним геометрический смысл комбинации сил и расстояний, составляющих момент. Работу при вращении производит тангенциальная (перпендикулярная радиусу) составляющая F t силы (рисунок).
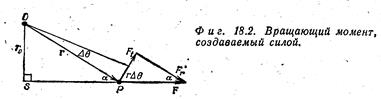
Выражаем работу через произведение силы на перемещение:
D А = Ft r Dq. Можно выразить работу и так: D А = F r sina = F r 0, где a - угол между направлением действия силы и радиусом, проведенным в точку ее приложения. Величина r 0 = r sina называется плечом силы F. Плечо силы - это расстояние между линией действия силы и осью вращения (рисунок).
Таким образом, сила оказывает на вращающееся тело тем большее действие, чем дальше от оси вращения расположена точка ее приложения.
Момент количества движения (момент импульса)
Теорема:
подобно тому, как внешняя сила равна скорости изменения величины р, которая называется полным импульсом системы частиц (второй закон Ньютона для системы частиц), так и момент силы равен скорости изменения некоторой величины L, называемой моментом количества движения, моментом импульса или угловым моментом группы частиц.
Для доказательства рассмотрим систему частиц, на которые действуют силы и посмотрим, что произойдет с системой в результате действия вращающих моментов, созданных этими силами.
Для начала возьмем одну частицу с массой m:
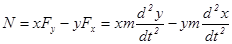
Надо увидеть, что это производная по времени от какой-то простой величины. Действительно, легко проверить, что:
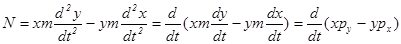
Таким образом, момент количества движения связан с компонентами импульса так же, как и момент силы с компонентами силы:
L = xpy - ypx; N = xFy - yFx
Угловой момент или момент количества движения показывает насколько быстро движется частица вокруг какого-то центра, ведь он учитывает только тангенциальную составляющую импульса. Кроме того, чем дольше от центра удалена линия, по которой направлен импульс, тем больше будет угловой момент. Существует (по аналогии с моментом силы) плечо импульса (не совпадает с плечом силы!):
L = xpy - ypx = r pt = p × (плечо импульса)
Закон сохранения момента количества движения
Распространим понятия момента сил и количества движения на систему частиц, взаимодействующих между собой и с внешними силами.
Сложим моменты сил всех частиц Ni и назовем это полным моментом сил .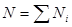
Сложим моменты количества движения всех частиц и назовем сумму полным моментом количества движения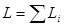 
Тогда:
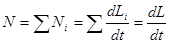
Полный момент сил N учитывает все внутренние и внешние силы. Однако, внутренние силы взаимно скомпенсируются и не внесут вклада в полный момент. Действительно, сила действия равна силе противодействия и действуют они вдоль одной прямой.
В результате доказана теорема:
скорость изменения момента количества движения относительно любой оси равна моменту внешних сил относительно этой оси.
Эта теорема верна для любого набора частиц, независимо от того, образуют они твердое тело или нет.
Закон сохранения момента количества движения:
если на систему частиц не действуют никакие внешние моменты сил, то ее момент количества движения остается постоянным.
Рассмотрим важный частный случай набора частиц - твердое тело. Посмотрим, как можно выразить момент количества движения L в этом случае. Разобьем тело на частицы mi, которые движутся по окружностям радиуса ri:
Li = mi vi ri =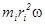 
L = I w, где за величину I, называемую моментом инерции, обозначили величину
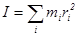
Момент инерции служит коэффициентом пропорциональности между моментом импульса и угловой скоростью, аналогично тому, как масса служит коэффициентом пропорциональности между импульсом и скоростью в случае поступательного движения. Таким образом, момент инерции отражает инерцию тела при вращательном движении. Из формулы для момента инерции видно, что инерция вращающегося тела зависит не только от его массы, а очень сильно зависит от того, насколько удалена масса тела от оси вращения.
Свойства момента инерции
Теорема Штейнера (теорема о параллельном переносе оси).
Момент инерции I относительно произвольной оси равен сумме момента инерции IC относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния а между осями:
I = IC + ma 2,
где I - момент инерции тела относительно данной произвольной оси;
ІC - момент инерции тела относительно оси, проходящей через центр масс и расположенной параллельно данной оси;
m - масса тела;
а - расстояние между данной осью и осью, проходящей через центр масс.
Для доказательства теоремы Штейнера рассмотрим ось С, проходящую через центр масс тела, и параллельную ей ось О, отстоящую от оси С на расстояние а (на рисунке обе оси перпендикулярны плоскости чертежа). Обозначим через R i перпендикулярный к оси С вектор, проведенный от оси к элементарной массе D mi, а через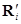 
-аналогичный вектор, проведенный от оси О. Введем также перпендикулярный к осям вектор а, соединяющий соответствующие точки осей О и С:
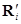= а + R i
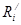2 = а 2 +2 а×R i + Ri 2
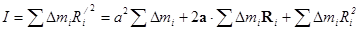
Первое слагаемое равно ma 2.
Сумма во втором слагаемом равна произведению массы тела на вектор R, проведенный от оси С к центру масс тела (согласно определению центра масс). Поскольку центр масс лежит на оси С, этот вектор R, а следовательно, и второе слагаемое равны 0.
Третье слагаемое равно ІC.
Таким образом, I = IC + ma 2.
Есть еще одно свойство момента инерции. Если имеется плоская фигура и тройка координатных осей с началом координат, расположенным в этой плоскости, и осью z, направленной перпендикулярно к ней, то момент инерции этой фигуры относительно оси z равен сумме моментов инерции относительно осей х и у:
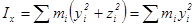(поскольку z = 0)
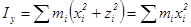
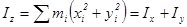
Кинетическая энергия вращения
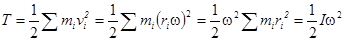
Как видим, наблюдается полная аналогия между формулами для одномерного поступательного и вращательного движения.
Силы инерции во вращающейся системе отсчета
Любая данная точка на вращающемся колесе движется относительно неподвижного наблюдателя с ускорением, направленным по радиусу к центру колеса и равным v 2/ R, где v - линейная скорость движения точки по окружности радиуса R. Если тело является неподвижным относительно колеса и находится в упомянутой точке, то оно должно двигаться с таким же ускорением. Это ускорение сообщается телу силой F = mv 2/ R, с которой на него действует колесо. Тело отвечает колесу силой противодействия такой же величины, противоположной по направлению (сила направлена по радиусу от центра вращения). С точки зрения наблюдателя, связанного с колесом, тело является неподвижным и на него действует сила F = mv 2/ R, направленная по радиусу от центра вращения. Эта сила называется центробежной силой инерции. Она уравновешивается реакцией опоры (колеса).
Центробежная сила является не единственной силой инерции во вращающейся системе отсчета. Если тело движется относительно вращающегося колеса, например, по радиусу от центра вращения со скоростью vr = dr / dt, то оно при этом должно увеличивать линейную скорость v = w r вращательного движения. Увеличение линейной скорости вращательного движения соответствует ускорению, направленному по касательной к окружности, перпендикулярно радиусу вращения. Это ускорение сообщается телу колесом. Тело отвечает колесу силой противодействия, которая, аналогично центробежной силе, является силой инерции и носит название силы Кориолиса. Она обладает странным свойством: оказывается, что если мы во вращающейся системе двигаем какой-то предмет, то сила Кориолиса толкает его вбок. Получим выражение для силы Кориолиса для упомянутого частного случая движения тела по радиусу от центра вращения.
Пусть тело движется по радиусу r вращающегося колеса. Момент импульса тела L = mvr = m w r 2. Если меняется r, то меняется L и, следовательно, должен действовать момент силы N = dL / dt:
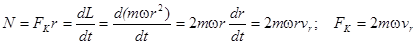
С кориолисовой силой мы встречаемся не только при движении тела относительно вращающейся системы отсчета, когда меняется радиус вращения. Можно показать, что если предмет m движется с постоянной скоростью vm по краю колеса, то на него тоже действует кориолисова сила. Почему? Наблюдатель на колесе видит предмет движущимся со скоростью vm, а неподвижный наблюдатель видит его движущимся по окружности со скоростью v = vm +w r, поскольку предмет вдобавок переносится колесом. Действующая в этом случае сила инерции будет центробежной силой mv 2/ r, которая соответствует скорости v. С точки зрения наблюдателя на колесе эта сила F будет состоять из трех частей:
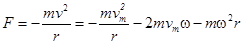
Первое слагаемое - это просто центробежная сила, которая должна возникнуть если побежать по кругу со скоростью vm. Эта сила не зависит от вращения колеса. Можно ожидать также появления центробежной силы, связанной с вращением колеса, которое осуществляется с угловой скоростью w (третье слагаемое). Однако, в добавление к этим центробежным силам прибавляется второе слагаемое. Раньше, при радиальной скорости, кориолисова сила была тангенциальной. Теперь же, при тангенциальной скорости, она радиальна. Видим, что сила всегда имеет одно и то же направление по отношению к скорости независимо от того, куда направлена скорость. Она действует под прямым углом к скорости и равна по величине 2 mv w.
Вращение в пространстве
Распространим математическое описание вращения, понятие момента количества движения, момента силы и т.д. на трехмерное пространство.
xFy - yFx так и остается моментом силы относительно оси z (плоскость вращения ху) и он равен скорости изменения момента импульса (xpy - ypx) относительно оси z:
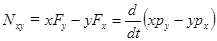ось z
Аналогично можно получить для оси х (плоскость вращения yz):
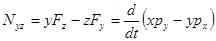ось х
Для оси у (плоскость вращения zx):
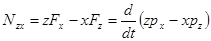ось у
Таким образом, имеются законы о том, что внешний момент сил в некоторой плоскости равен скорости изменения углового момента в этой плоскости.
А если повернуть оси, например, в плоскости х, у. Новые координаты назовем х /, у /. Новый момент сил в этой плоскости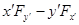 
. Найдем связь между новыми и старыми моментами. Это похоже на манипуляции с векторами. - Да. А не вектор ли момент сил? - Да. Докажем это.
Пусть ось z останется той же. Поворачиваем х и у на угол q. Законы преобразования координат мы рассматривали раньше:
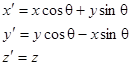
Поскольку сила является вектором, закон преобразования ее компонент такой же:
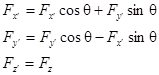
Подставляем уравнения преобразования координат и силы в выражения для моментов силы (промежуточные преобразования опускаем):
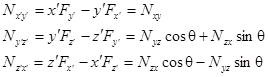
Можно увидеть связь между законами преобразования моментов силы и законами преобразования координат. Если назвать Nxy z -компонентой Nz вектора N, аналогично, если связать плоскость yz с х -компонентой новоиспеченного вектора N, а плоскость zx с у -компонентой, то закон преобразования будет выглядеть так:
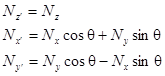
что в точности соответствует закону преобразования векторов.
Следовательно, доказано, что комбинацию xFy - yFx можно отождествить с тем, что обычно называется z -компонентой некоторого искусственно введенного вектора. Хотя момент сил является своего рода «кручением» в плоскости и, казалось бы, не имеет векторного характера, математически он все-таки ведет себя как вектор. Этот вектор направлен под прямым углом к плоскости кручения, а его длина пропорциональна силе кручения. Три компоненты такой величины будут преобразовываться при вращении системы координат как самый настоящий вектор.
Итак, мы представляем момент силы в виде вектора. Согласно правилу, с каждой плоскостью, в которой он действует, мы связываем прямую, перпендикулярную к этой плоскости. Однако перпендикулярность к плоскости оставляет неопределенный знак вектора. Чтобы определить его, необходимо еще одно дополнительное правило, которое говорило бы нам, что если момент силы действует определенным образом в плоскости ху, то соответствующий ему вектор направлен «вверх» по оси z. Предположим, что система координат хуz правосторонняя (если вращать ось х по направлению к оси у, то направление, связанного с таким вращением, поступательного движения винта с правовинтовой резьбой, укажет положительное направление оси z). Тогда правило должно быть таким: если представить себе кручение, как ввертывание болта с правовинтовой резьбой, то направление вектора, связанного с этим кручением, определяется поступательным движением болта.
Векторное произведение
В предыдущих рассуждениях совершенно несущественно, что х - координата, F -сила, а существенным является закон преобразования векторов. Значит, например, (axby - aybx) можно связать с z -компонентой какого-то вектора с и т.д. Можно придумать для такой связи название и обозначение:
векторное произведение с = а ´ b = [ a, b ],
что расшифровывается:
cx = aybz - azby
cy = azbx - axbz
cz = axby - aybx
Свойства векторного произведения
а ´ b = -b ´ a
Отсюда:
а ´ а = 0
Результатом векторного произведения есть вектор, который перпендикулярен обоим перемножаемым векторам: с ^ а, с ^ b. Доказательством является равенство нулю скалярных произведений с × а и с × b (скалярные произведения можно расписать как сумму произведений одноименных проекций векторов).
Модуль векторного произведения равен произведению модулей векторов на синус угла между ними: ÷ а ´ b ê= а b sina. Это правило легко доказывается путем вычисления результата векторного произведения через проекции векторов для простейшего частного случая: вектор а смотрит из начала координат в направлении оси х (аy и az = 0; ax = a), вектор b -расположен в плоскости ху (bz = 0). Поскольку результат векторного произведения не зависит от выбора системы координат (это свойство любого вектора, для этого они и придуманы), правило можно распространить на произвольную систему координат.
Способ определения направления вектора, являющегося результатом векторного произведения: если вращать вектор а (первый из перемножаемых векторов) по направлению к вектору b (второй из перемножаемых векторов), то вектор c = а ´ b будет направлен в сторону поступательного движения, связанного с этим вращением, винта с правой резьбой. Это простая договоренность. Получается, что результатом векторного произведения является не совсем «честный» вектор. Такие вектора называются аксиальными, или псевдовекторами, в отличие от обычных полярных векторов. Аксиальные вектора хорошо передают свойства вращения.
Приводим без доказательства сводку правил векторной алгебры:
A×B =Скаляр=AxBx+AyBy+AzBz,
A´B =Вектор,
(A´B)z=AxBy-AyBx,
(A´B)x=AyBz-AzBy,
(A´B)y=AzBx-AxBz,
A´A =0,
A× (A´B)=0,
A× (B´C)=(A´B) ×C,
A´ (B´C)= B (A×C)- C (A×B)