Матрицы и действия с ними
Основные определения
Прямоугольная таблица чисел
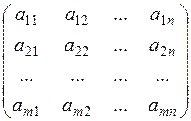, (4.1)
содержащая 
строк и 
столбцов, называется матрицей размером 
. Числа 
называются элементами матрицы.
Две матрицы 
и 
считаются равными, если совпадают их размеры и 
при любых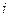 
и 
.
Наряду с матрицей
часто приходится рассматривать матрицу, столбцами которой являются строки матрицы 
(т.е. столбцы и строки меняются местами). Эта матрица называется транспонированной к 
и обозначается через 
:
.
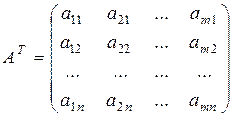Если число строк матрицы равно числу ее столбцов, то матрица называется квадратной, а число 
ее строк (равное числу столбцов) – порядком квадратной матрицы. Диагональ 
квадратной матрицы называется главной диагональю, а диагональ 
– побочной диагональю.
Квадратная матрица называется треугольной, если все ее элементы, которые находятся ниже (или выше) главной диагонали, равны нулю, т.е. треугольная матрица имеет вид
или 
.
При этом матрицу называют верхнетреугольной, а матрицу 
– нижнетреугольной.
Матрица E вида
называется единичной матрицей. Легко проверить, что для любой матрицы -го порядка имеют место равенства
.
Действия с матрицами.
1) Умножение матрицы на число. Для того чтобы умножить матрицу на число 
, нужно каждый элемент матрицы умножить на это число: 
.
2) Сложение матриц. Складывать можно только матрицы с одинаковым числом строк и столбцов, т.е. матрицы одинаковых размеров. Суммой матриц и называется матрица 
, элементы которой равны суммам соответствующих элементов матриц и 
, т.е. 
для любых индексов 
, 
.
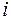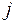3) Умножение матриц. Произведение матрицы на матрицу (обозначается 
) определено только в том случае, когда число столбцов матрицы равно числу строк матрицы . В результате умножения получим матрицу 
, у которой столько же строк, сколько их в матрице , и столько же столбцов, сколько их в матрице . Для удобства запоминания запишем это кратко:
Есл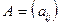и 
, и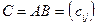 
, то элементы 
определяются следующим образом:
, (4.2)
где 
.
В качестве примера применения указанного правила приведем формулу перемножения квадратных матриц 2-го порядка:
.
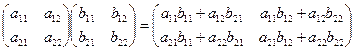Определители
Основные определения.
Перестановкой чисел 1, 2,..., n называется любое расположение этих чисел в определенном порядке. Число всех перестановок, которые можно образовать из n чисел, равно 
. Например, из трех чисел 1, 2, 3 можно образовать 3!=6 перестановок: 123, 132, 312, 321, 231, 213. Говорят, что в данной перестановке числа i и j составляют инверсию (беспорядок), если i>j, но i стоит в этой перестановке раньше j, то есть если большее число стоит левее меньшего.
Обозначим общее число инверсий в перестановке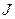 
символом 
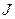. Перестановка называется четной, если число – четное, и нечетной, если число – нечетное.
Так в рассмотренном выше примере перестановка содержала 3 инверсии и, следовательно, является нечетной. Заметим, что перестановка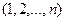 
не содержит ни одной инверсии, иначе говоря, содержит 0 инверсий. Следовательно, эта перестановка является четной.
Определителем -го порядка (или определителем квадратной матрицы -го порядка) называется число, равное
, (4.3)
где суммирование распространяется на все перестановки 
, которые можно составить из чисел 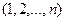. Количество слагаемых в правой части равенства (4.3) равно 
, так как количество всех перестановок множества из элементов равно 
Правила вычисления определителей 2-го и 3-го порядков легко выписать:
,
Приведенное правило вычисления определителей 3-го порядка называется правилом треугольников.
Свойства определителей
1. Определитель не меняется при транспонировании.
2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.
3. Если в определителе переставить две строки, определитель поменяет знак.
4. Определитель, содержащий две одинаковые строки, равен нулю.
5. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k.
6. Определитель, содержащий две пропорциональные строки, равен нулю.
7. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых ai j = bj + cj (j= 
), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj.
8. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.
Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.
Минором Mij элемента aij определителя 
n-го порядка называется определитель порядка n-1, который получается из вычеркиванием строки и столбца, содержащих данный элемент.
Алгебраическим дополнением элемента aij определителя называется его минор Mij, взятый со знаком (-1) i + j. Алгебраическое дополнение элемента aij будем обозначать Aij. Таким образом, Aij = (-1) i + j Mij.
На практике определители удобно находить, используятеорему оразложенииопределителя по строке или столбцу:
Теорема (разложение определителя по строке или столбцу).
Определитель равен сумме произведений всех элементов его произвольной строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение определителя d по элементам i-й строки
= ai 1 Ai 1 + ai 2 Ai 2 +... + ai n Ai n (i = )
или j- го столбца
= a1 j A1 j + a2 j A2 j +... + an j An j (j = ).
В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.
В дальнейшем i -ую строку определителя или матрицы будем обозначать Si, а j-ый столбец - Сj.
Обратная матрица и способы ее нахождения
Основные определения.
Рассмотрим квадратную матрицу
A = 
.
Обозначим D =det A.
Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если D = 0.
Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В.
Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
Матрица, обратная матрице А, обозначается через А-1, так что В = А-1. Обратная матрица вычисляется по формуле
А-1 = 1/D 
, (4.4)
где А i j - алгебраические дополнения элементов a i j.
Вычисление обратной матрицы по формуле (4.4) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП).
Элементарными называются следующие преобразования матрицы:
1) перестановка двух любых строк (или столбцов),
2) умножение строки (или столбца) на отличное от нуля число,
3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту, но в процессе преобразований следует использовать только операции над строками.
Ранг матрицы
Основные определения.
Рассмотрим прямоугольную матрицу (4.1). Если в этой матрице выделить произвольно k строк и k столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел m и n. Среди всех отличных от нуля миноров матрицы А найдется по крайней мере один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен r, то это означает, что в матрице А имеется отличный от нуля минор порядка r, но всякий минор порядка, большего чем r, равен нулю. Минор порядка r называется базисным. Ранг матрицы А обозначается через r(A). Очевидно, что выполняется соотношение
0 £ r(A) £ min (m, n).
Ранг матрицы находится либо методом окаймления миноров (перебора миноров и выбора из них ненулевого минора наибольшего порядка), либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A ~ B.
С помощью элементарных преобразований матрицу можно привести к виду
,
в котором элементы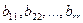 
отличны от нуля, а элементы, расположенные ниже, равны нулю. Матрицу 
такого вида называют ступенчатой. После приведения матрицы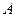 
к ступенчатому виду можно сразу записать, что 
.
В самом деле, 
(т.к. элементарные преобразования не меняют ранга). Но у матрицы существует отличный от нуля минор порядка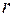 
:
,
а любой минор порядка 
содержит нулевую строку и поэтому равен нулю.
Сформулируем теперь практическое правило вычисления ранга матрицы 
с помощью элементарных преобразований: для нахождения ранга матрицы следует с помощью элементарных преобразований привести ее к ступенчатому виду 
. Тогда ранг матрицы будет равен числу ненулевых строк в полученной матрице 
.