Сущность метода Гаусса заключается в том, что с помощью элементарных преобразований расширенная матрица системы приводится к ступенчатому виду (производя при этом элементарные преобразования только над строками матрицы). Причем выделяют две стадии метода Гаусса: прямой ход, когда мы «обнуляем» элементы под «диагональными» элементами, и обратный ход, когда мы «обнуляем» элементы над «диагональными». Можно сразу обнулять элементы столбцов как ниже главной диагонали, так и выше. В этом случае «обратного хода» не требуется. Такая модификация метода называется метод Гаусса-Жордана. Если ранг матрицы r меньше числа неизвестных n, то необходимо выделить базисный минор матрицы системы. Тогда столбцы, из которых выделяется базисный минор, будут определять базисные переменные, а оставшиеся – свободные переменные. Рассмотрим алгоритм применения метода Гаусса на простых примерах.
Примеры решения задач
Пример 1. Даны две матрицы A и B. Найти: AB
А=  , В =
, В =  .
.
Решение. Поскольку матрица А размера 2´3, матрица В размера 3´3, то произведение АВ = С существует и элементы матрицы С равны
с11 = 1×1 +2×2 + 1×3 = 8, с21 = 3×1 + 1×2 + 0×3 = 5, с12 = 1×2 + 2×0 + 1×5 = 7,
с22 =3×2 + 1×0 + 0×5 = 6, с13 = 1×3 + 2×1 + 1×4 = 9, с23 = 3×3 + 1×1 + 0×4 = 10.
AB = 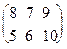 , а произведение B A не существует.
, а произведение B A не существует.
Пример 2.. Найти АВТ, если А = 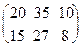 , В = (50 70 130).
, В = (50 70 130).
Решение. АВT = 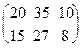
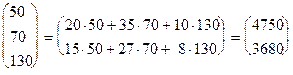 .
.
Пример 3. Даны две матрицы A и B. Найти: а)AB; б)BA; в)3АВ-2А
A = 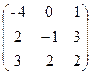 , B =
, B = 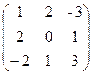 .
.
Решение:
а) Произведение АВ имеет смысл, так как число столбцов матрицы А равно числу строк матрицы В. Находим матрицу С=АВ, элементы которой определяются по формуле cij =ai1b1j+. ai2b2j+ ai3b3j+. …+ ainbnj. Имеем:
AB= 
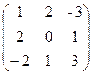 =.
=.  =
= 
б) Вычислим BA=  .
. 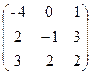 ==.
==. 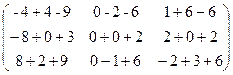 =
= 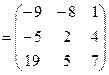
Очевидно, что; AB  BA
BA
в)Вычислим 3АВ-2А, используя полученный результат для АВ из пункта а)
3АВ-2А = 3 
 - 2
- 2 
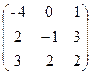 =
=  -
-  =
= 
Пример 4. Найти BACT + BADT, если A = 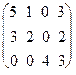 , B= (10 15 23),
, B= (10 15 23),
C= (40 35 24 16), D= (5 3 2 2).
Решение.
BА=(10 15 23) 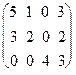 =
=  =
=
=(95 40 92 129).
B А C T = (95 40 92 129) 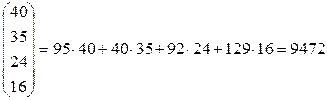 .
.
BАD T = (95 40 92 129) 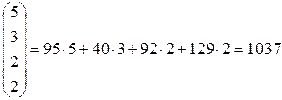 .
.
Итак, BАC T + BАD T = 9472 + 1037 = 10509
Пример 5. Найти B3, если 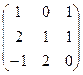
Решение. Сначала найдем В2=В B= 
 =
=  .
.
В3=В В2 = 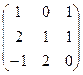
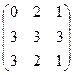 =
= 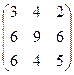 .
.
Легко убедиться, что В3=В2 В = 
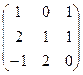 =
=  , что подтверждает правильность сочетательного закона при умножении матриц.
, что подтверждает правильность сочетательного закона при умножении матриц.
Пример 6. Для данного определителя  :
:
1) найти миноры и алгебраические дополнения элементов a12 и a32.
2) Вычислить определитель: а) разложив его по элементам 1-ой строки; б) разложив его по элементам 2-го столбца; в) получив предварительно нули в 1-ой строке.
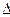 =
= 
Решение:
1). Находим миноры к элементам a12 и a32 по правилу треугольников:
M12 = 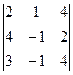 = -8-16+6+12+4-16=-18,
= -8-16+6+12+4-16=-18,
M32 = 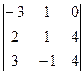 =-12+12=12-8=-20.
=-12+12=12-8=-20.
Алгебраические дополнения элементов a12 и a32 соответственно равны:
A12 =(-1)1+2 M12 –(-18)=18,
A32 =(-1)3+2 M32 –(-20)=20,
2) а). Вычислим определитель, разложив его по элементам первой строки:
 = a1 1 A11j + a12 A12 + a13 A13 + a14 A14 =-3
= a1 1 A11j + a12 A12 + a13 A13 + a14 A14 =-3 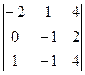 - 2
- 2 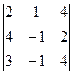 + 1
+ 1 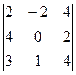 - +0
- +0 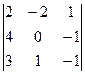 -= -3(8 + 2 + 4 – 4) - -2(-8 – 16 + 6 + 12 +4 + 16) + (16 – 12 – 4 + 32) = 38.
-= -3(8 + 2 + 4 – 4) - -2(-8 – 16 + 6 + 12 +4 + 16) + (16 – 12 – 4 + 32) = 38. 
б) Вычислим определитель, разложив его по элементам второго столбца:
 = a2 1 A21 + a22 A22 + a23 A23 + a24 A24 =-2
= a2 1 A21 + a22 A22 + a23 A23 + a24 A24 =-2 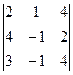 - 2
- 2 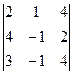 +
+
+0 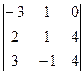 +1
+1 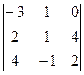 = -2(-8 + 6 - 16 +12 +4 - 16) – 2(12+ 6 – 6 – 16) + (-6 + 16 - - 12 – 4)=38.
= -2(-8 + 6 - 16 +12 +4 - 16) – 2(12+ 6 – 6 – 16) + (-6 + 16 - - 12 – 4)=38.
в) Вычислим определитель  , получив предварительно нули в первой строке. Используем свойство определителей: определитель не изменится, если ко всем элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же произвольное число. Умножим третий столбец определителя на 3 и прибавим к первому (3C3+C1).Полученный столбец запишем вместо первого. Затем третий столбец умножим на (-2) и прибавим ко второму (-2C3+C2.), и полученный столбец запишем вместо второго. Тогда в первой строке все элементы, кроме одного, будут нулями. Разложим полученный таким образом определитель по элементам первой строки и вычислим его:
, получив предварительно нули в первой строке. Используем свойство определителей: определитель не изменится, если ко всем элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же произвольное число. Умножим третий столбец определителя на 3 и прибавим к первому (3C3+C1).Полученный столбец запишем вместо первого. Затем третий столбец умножим на (-2) и прибавим ко второму (-2C3+C2.), и полученный столбец запишем вместо второго. Тогда в первой строке все элементы, кроме одного, будут нулями. Разложим полученный таким образом определитель по элементам первой строки и вычислим его:
 =
=  =
=  =
= 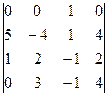 = 1*
= 1* 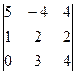 .= =
.= =  =
= 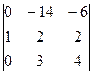 = -(-56+18)=38
= -(-56+18)=38
Пример7. Не вычисляя определителя 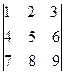 , показать, что он равен нулю.
, показать, что он равен нулю.
Решение. Вычтем из второй строки первую, получим определитель 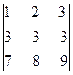 , равный исходному. Если из третьей строки также вычесть первую, то получится определитель
, равный исходному. Если из третьей строки также вычесть первую, то получится определитель 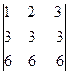 , в котором две строки пропорциональны. Такой определитель равен нулю.
, в котором две строки пропорциональны. Такой определитель равен нулю.
Пример 8. Вычислить определитель D = 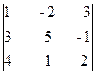
а) разложив его по элементам второго столбца,
б) по правилу треугольников.
Решение.
а) Разложим определитель по элементам второго столбца:
D = a12A12 + a22A22+a32A32=
= 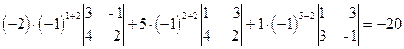 .
.
б) По правилу треугольников:
D = 10+8+9-60+12+1 = -20.
Пример 9. Вычислить определитель А, в котором все элементы по одну сторону от главной диагонали равны нулю.
А = 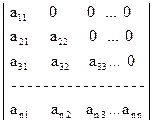 ,
,
Решение. Разложим определитель А по первой строке:
A = a11 A11 = 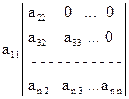 .
.
Определитель, стоящий справа, можно снова разложить по первой строке, тогда получим:
A = 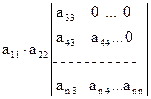 .
.
И так далее. После n шагов придем к равенству A = а11 а22... ann.
Пример 10. Вычислить определитель  .
.
Решение. Если к каждой строке определителя, начиная со второй, прибавить первую строку, то получится определитель, в котором все элементы, находящиеся ниже главной диагонали, будут равны нулю. А именно, получим определитель: 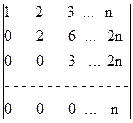 , равный исходному.
, равный исходному.
Рассуждая, как в предыдущем примере найдем, что он равен произведению элементов главной диагонали, т.е. n!. Способ, с помощью которого вычислен данный определитель, называется способом приведения к треугольному виду.
Пример11. Для матрицы А = 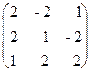 найти обратную.
найти обратную.
Решение. Находим сначала детерминант матрицы А
D = det А =  = 27 ¹ 0, значит, обратная матрица существует и мы ее можем найти по формуле: А-1 = 1/D
= 27 ¹ 0, значит, обратная матрица существует и мы ее можем найти по формуле: А-1 = 1/D  , где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j исходной матрицы. Имеем:
, где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j исходной матрицы. Имеем: 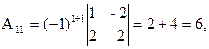
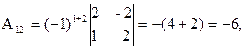
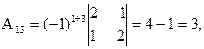
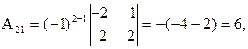
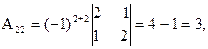
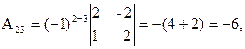
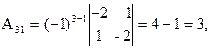

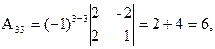 откуда
откуда
А-1 =  .
.
Проверим равенство АА-1=Е


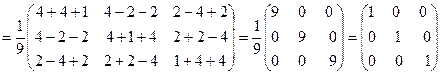
Пример12. Методом элементарных преобразований найти обратную матрицу для матрицы: А= 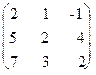 .
.
Решение. Приписываем к исходной матрице справа единичную матрицу того же порядка: 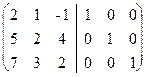 . С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие же преобразования над правой матрицей.
. С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие же преобразования над правой матрицей.
Для этого поменяем местами первый и второй столбцы: 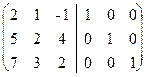 ~
~ 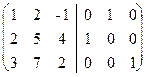 . К третьему столбцу прибавим первый, а ко второму - первый, умноженный на -2:
. К третьему столбцу прибавим первый, а ко второму - первый, умноженный на -2: 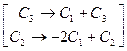

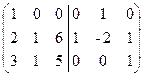 . Из первого столбца вычтем удвоенный второй, а из третьего - умноженный на 6 второй:
. Из первого столбца вычтем удвоенный второй, а из третьего - умноженный на 6 второй: 

 . Прибавим третий столбец к первому и второму:
. Прибавим третий столбец к первому и второму: 

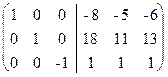 . Умножим последний столбец на -1:
. Умножим последний столбец на -1: 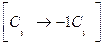

 . Полученная справа от вертикальной черты квадратная матрица является обратной к данной матрице А. Итак,
. Полученная справа от вертикальной черты квадратная матрица является обратной к данной матрице А. Итак,
А-1 = 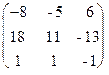 .
.
Сделаем проверку А-A-1-= 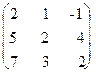
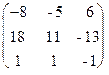 =
= 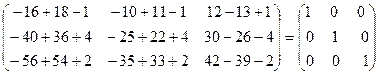 .
.
Пример 13. Методом элементарных преобразований найти обратную матрицу для матрицы: А=  .
.
Решение. Приписываем к исходной матрице справа единичную матрицу того же порядка и контрольный столбец:  . С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие же преобразования над правой матрицей:
. С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие же преобразования над правой матрицей:
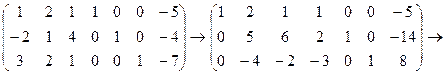
Вместо второй строки напишем сумму третьей и второй строк:


Итак,
А-1 =  .
.
Пример 14. Найти методом окаймления миноров ранг матрицы 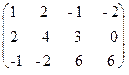 и написать один из базисных миноров.
и написать один из базисных миноров.
Решение: Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) М1 = 1, расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор M2 = 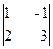 , отличный от нуля. Переходим теперь к минорам 3-го порядка, окаймляющим М2. Их всего два (можно
, отличный от нуля. Переходим теперь к минорам 3-го порядка, окаймляющим М2. Их всего два (можно
добавить второй столбец или четвертый). Вычисляем их:  = 0. Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум а базисным минором будет, например M2 =
= 0. Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум а базисным минором будет, например M2 =  .
.
Пример15. Найти ранг матрицы А=  и привести ее к ступенчатому виду.
и привести ее к ступенчатому виду.
Решение: Из второй строки вычтем первую и переставим эти строки: 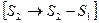 ~
~ 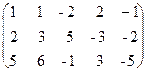 . Теперь из второй и третьей строк вычтем
. Теперь из второй и третьей строк вычтем  первую, умноженную соответственно на 2 и 5
первую, умноженную соответственно на 2 и 5  ~:
~: 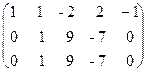 ; из третьей строки вычтем первую; получим матрицу В =
; из третьей строки вычтем первую; получим матрицу В = 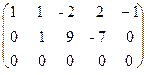 , которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2. Базисным минором является минор
, которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2. Базисным минором является минор 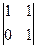 .
.
Пример 16. Исследовать систему уравнений на совместность:

Решение: Выписываем расширенную матрицу системы:
`A = 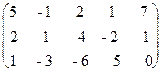 .
.
Вычислим ранг основной матрицы системы. Очевидно, что, например, минор второго порядка в левом верхнем углу  = 7 ¹ 0; содержащие его миноры третьего порядка равны нулю:
= 7 ¹ 0; содержащие его миноры третьего порядка равны нулю:
M¢3 = 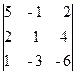 = 0, M²3 =
= 0, M²3 = 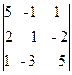 = 0.
= 0.
Следовательно, ранг основной матрицы системы равен 2, т.е. r(A)=2. Для вычисления ранга расширенной матрицы `A рассмотрим окаймляющий минор
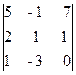 =
= 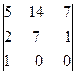 = -35 ¹ 0,
= -35 ¹ 0,
значит, ранг расширенной матрицы r(`A) = 3. Поскольку r(A) ¹ r(`A), то система несовместна.
Пример 17. Решить методом Крамера систему уравнений:

Решение: Главный определитель этой системы
D =  = -142 ¹ 0,
= -142 ¹ 0,
значит, система имеет единственное решение. Вычислим вспомогательные определители D i (i=  ), получающиеся из определителя D путем замены в нем столбца, состоящего из коэффициентов при xi, столбцом из свободных членов:
), получающиеся из определителя D путем замены в нем столбца, состоящего из коэффициентов при xi, столбцом из свободных членов:
D 1 =  = - 142, D 2 =
= - 142, D 2 = 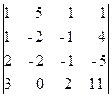 = - 284,
= - 284,
D 3 =  = - 426, D 4 =
= - 426, D 4 =  = 142.
= 142.
Отсюда x1 = D 1/D = 1, x2 = D 2/D = 2, x3 = D 3/D = 3, x4 = D 4/D = -1, решение системы - вектор С=(1, 2, 3, -1)T.
Пример 18. Решить методом Крамера систему уравнений:.

Решение: Как и в предыдущем примере, найдем главный определитель и вспомогательные определители
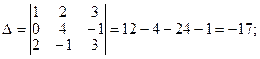
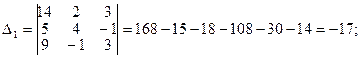

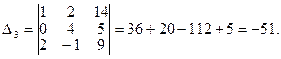
Находим решение системы:
x1 = D 1/D = -  = 1, x2 = D 2/D =
= 1, x2 = D 2/D = 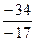 = 2, x3 = D 3/D =
= 2, x3 = D 3/D =  = 3.
= 3.
Пример 19. Решить матричным способом систему уравнений

Решение: Обозначим
A = 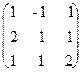 ,
,  , B =.
, B =. 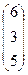 .
.
Тогда данная система уравнений запишется матричным уравнением AX=B. Поскольку D = det 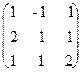 =5 ¹ 0, то матрица A невырожденная и поэтому имеет обратную:
=5 ¹ 0, то матрица A невырожденная и поэтому имеет обратную:
А-1 = 1/D  , где.
, где. 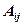 - алгебраическое дополнение к элементу
- алгебраическое дополнение к элементу 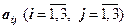 .
.
Для получения решения X мы должны умножить вектор-столбец B слева на матрицу A: X = A-1B. В данном случае
A-1 = 
и, следовательно,
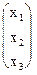 =
= 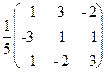
 .
.
Выполняя действия над матрицами, получим:
x1 = 1/5(1×6+3×3-2×5) = 1/5 (6+9-10) = 1,
x2 = 1/5 (-3×6 +1×3 - 1×5) = 1/5 (- 18 + 3 + 5) = -2,
x3 = 1/5 (1×6 - 2×3 + 3×5) = 1/5 (6 -6 + 15) = 3.
Итак, X = (1, -2, 3)T.
Пример 19. Решить матричным способом систему уравнений, при этом проверив правильность вычисления обратной матрицы

Решение: Для нахождения решения с помощью обратной матрицы запишем систему уравнений в матричной форме AX=B, где
 ,
,  ,
, 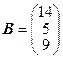 .
.
Как и в предыдущем примере D = det 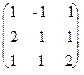 =-17 ¹ 0, поэтому матрица A невырожденная и поэтому имеет обратную. Решение системы в матричной форме имеет вид
=-17 ¹ 0, поэтому матрица A невырожденная и поэтому имеет обратную. Решение системы в матричной форме имеет вид 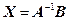 , где
, где 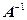 - матрица, обратная матрице
- матрица, обратная матрице  . Найдем матрицу
. Найдем матрицу 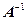 по формуле
по формуле
А-1 = 1/D 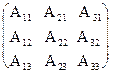 ., где
., где  =17,
=17, 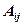 - алгебраическое дополнение к элементу
- алгебраическое дополнение к элементу 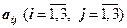 .
.
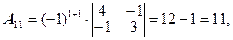
| 
| 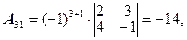
|
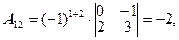
| 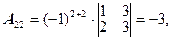
| 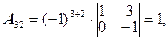
|
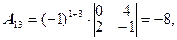
| 
| 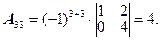
|
Обратная матрица имеет вид: 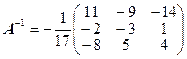 .
.
Проверим правильность нахождения обратной матрицы:


Находим решение системы.
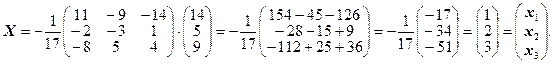
Итак, решение системы: 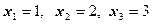 .
.
Пример 20. Решить систему линейных алгебраических уравнений методом Гаусса:

Решение. Преобразуем расширенную матрицу системы:
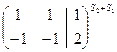 ~
~  .
.
Отсюда следует, что 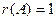 ,
, 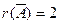 , т.е. исходная система несовместна. Заметим, что, применяя метод Гаусса (т.е. исключая неизвестные), мы одновременно проводим исследование системы на совместность (т.е. отыскиваем ранги матрицы системы и расширенной матрицы).
, т.е. исходная система несовместна. Заметим, что, применяя метод Гаусса (т.е. исключая неизвестные), мы одновременно проводим исследование системы на совместность (т.е. отыскиваем ранги матрицы системы и расширенной матрицы).
Пример 21. Решить систему линейных алгебраических уравнений методом Гаусса:
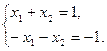
Решение: Исследуем систему на совместность:
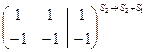 ~
~  ~
~ 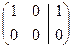 .
.
Отсюда следует, что 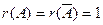 – система совместна.
– система совместна.
Поскольку ранг матрицы меньше числа неизвестных, то система имеет бесчисленное множество. Базисный минор |1| выделяется только из первого столбца, поэтому первая переменная x1 - базисная, а вторая x2 свободная. Обозначая x2 = t, получаем общее решение системы: x1= t, x2 =t или в векторном виде  , где t - произвольная постоянная.
, где t - произвольная постоянная.
Придавая t различные действительные значения, получаем бесконечное множество решений исходной системы.
Пример 22. Решить однородную систему линейных алгебраических уравнений методом Гаусса:

Решение: Однородная система всегда является совместной, т.к имеет нулевое (или тривиальное) решение: 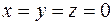 . Поэтому для однородных систем особый интерес представляет вопрос о существовании ненулевых (или нетривиальных) решений.
. Поэтому для однородных систем особый интерес представляет вопрос о существовании ненулевых (или нетривиальных) решений.
Преобразуем расширенную матрицу системы:
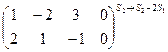 ~
~ 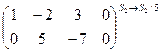 ~
~ 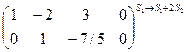 ~ ~
~ ~ 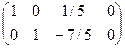 .
.
Имеем 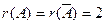 – система совместна. В качестве базисного минора выбираем
– система совместна. В качестве базисного минора выбираем  , отвечающий переменным x1 и x2. Тогда переменная x3 - свободная переменная. Полагая x3
, отвечающий переменным x1 и x2. Тогда переменная x3 - свободная переменная. Полагая x3 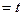 (где t – произвольная постоянная), получим
(где t – произвольная постоянная), получим

Отсюда 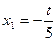 ,
,  . Таким образом, общее решение системы имеет вид
. Таким образом, общее решение системы имеет вид
 , где t – произвольная постоянная.
, где t – произвольная постоянная.
Пример 23. Решить систему линейных алгебраических уравнений методом Гаусса:
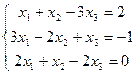
Решение: Выпишем расширенную матрицу данной системы
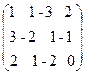
и произведем следующие элементарные преобразования над ее строками: из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2, затем третью строку умножим на (-5) и прибавим к ней вторую:
 ~
~ 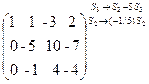 ~
~ 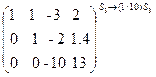 ~
~  .
.
Имеем 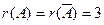 – система совместна и имеет единственное решение (ранг совпадает с числом неизвестных). Поэтому все переменные будут базисными и переходим к обратному ходу метода Гаусса, т.е. обнуляем элементы над главной диагональю:
– система совместна и имеет единственное решение (ранг совпадает с числом неизвестных). Поэтому все переменные будут базисными и переходим к обратному ходу метода Гаусса, т.е. обнуляем элементы над главной диагональю:
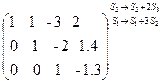 ~
~ 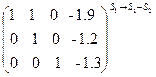 ~
~ 
 .
.
В результате всех этих преобразований x1=-0.7, x2=-1.2, x3=-1.3, или в векторном виде
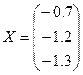 .
.
Пример 24. Решить однородную систему линейных алгебраических уравнений
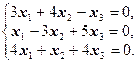
Решение: Запишемсистему в матричной форме AX=B, где
 ,
,  ,
, 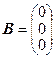 .
.
При помощи элементарных преобразований строк приведем расширенную матрицу системы к ступенчатому виду. Поменяем местами первую и вторую строки матрицы
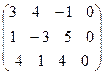 ~
~  .
.
Умножим первую строку на -3 и прибавим ко второй строке. Умножим первую строку на -4 и прибавим к третьей строке:
 .
.
Сложим вторую и третью строки, а затем разделим вторую строку на 13:
.  ~
~ 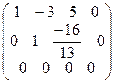 .
.
Полученная матрица является ступенчатой, содержит две ненулевые строки, поэтому 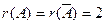 .
.
Так как ранг матриц меньше числа неизвестных, то система имеет бесконечное множество решений. В качестве базисного минора можно взять М= =  =1
=1  , который содержит 1-ый и 2-ой столбцы матрицы. Поэтому переменные
, который содержит 1-ый и 2-ой столбцы матрицы. Поэтому переменные 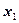 и
и 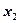 возьмем в качестве базисных, а переменная
возьмем в качестве базисных, а переменная  будет свободной. Далее, используя процедуру обратного хода метода Гаусса обнуляем верхнюю часть матрицы (т. е элемент а12 ), умножив вторую строку на 3 и сложив ее со второй строкой
будет свободной. Далее, используя процедуру обратного хода метода Гаусса обнуляем верхнюю часть матрицы (т. е элемент а12 ), умножив вторую строку на 3 и сложив ее со второй строкой

Полагая x3 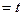 (где t – произвольная постоянная), получим
(где t – произвольная постоянная), получим

Отсюда 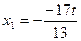 ,
, 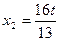 . Таким образом, общее решение системы имеет вид
. Таким образом, общее решение системы имеет вид
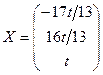 , где t – произвольная постоянная.
, где t – произвольная постоянная.
Пример 25. Решить систему линейных алгебраических уравнений методом Гаусса:
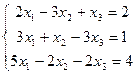
Решение: Выпишем расширенную матрицу данной системы
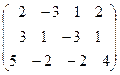
Преобразуем ее следующим образом: из третьей строки вычитаем первую и вторую строки, затем к первой строки прибавляем вторую, умноженную на 3:
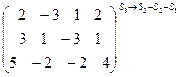 ~
~ 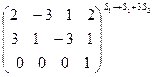 ~
~  .
.
Теперь ясно, что 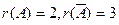 . Согласно теореме Кронекера - Капелли, из того, что
. Согласно теореме Кронекера - Капелли, из того, что  , следует несовместность исходной системы.
, следует несовместность исходной системы.