Основное уравнение динамики точки имеет вид
 , (4) где
, (4) где  - равнодействующая сил, действующих на точку.
- равнодействующая сил, действующих на точку.
Дифференциальные уравнения движения точки в проекциях на декартовые оси записываются:
 , (5) здесь
, (5) здесь 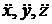 проекции ускорения
проекции ускорения  - проекции равнодействующей на соответствующие оси.
- проекции равнодействующей на соответствующие оси.
В проекциях на подвижные естественные оси 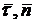 и
и  динамические уравнения движения точки записываются в форме:
динамические уравнения движения точки записываются в форме:
 , (6) где
, (6) где  - проекция скорости на направление касательной к траектории,
- проекция скорости на направление касательной к траектории,  - модуль скорости,
- модуль скорости, 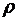 - радиус кривизны траектории в данной точке,
- радиус кривизны траектории в данной точке,  - проекции равнодействующей на естественные оси.
- проекции равнодействующей на естественные оси.
С помощью дифференциальных уравнений движения материальной точки можно решать две основные задачи динамики: прямую и обратную.
К первой (прямой) задаче динамики точки относятся задачи, в которых по заданному движению точки требуется определить равнодействующую сил, приложенных к точке. Это задача решается посредством дифференцирования заданных уравнений движения точки.
Ко второй (обратной) задаче динамики точки относятся те задачи, в которых определяется движение точки по заданным силам. Решение второй задачи динамики точки сводится к интегрированию системы дифференциальных уравнений движения точки (5).
При интегрировании системы уравнений (5) в общем случае появляются шесть произвольных постоянных, которые определяют по начальным условиям. Под начальными условиями движения точки понимают значения координат и проекций скорости точки в начальный момент движения, т.е. при  :
:
 (7)
(7)
Если движение точки происходит в плоскости, то число уравнений (5) сокращается до двух, а при движении точки по прямой будет одно дифференциальное уравнение и два начальных условия.
Пример выполнения задания
Груз D массой m = 2 кг движется в вертикальной плоскости в изогнутой трубе АВС, получив в точке А скорость  (рис. 31). На участке АВ на груз, кроме силы тяжести, действует сила
(рис. 31). На участке АВ на груз, кроме силы тяжести, действует сила 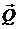 (её направление показано на рисунке), причём Q = 2 Н, сила сопротивления среды
(её направление показано на рисунке), причём Q = 2 Н, сила сопротивления среды  , коэффициент трения груза о трубу f 1 = 0,1, AB = l = 2,5 м.
, коэффициент трения груза о трубу f 1 = 0,1, AB = l = 2,5 м.
Не изменяя величины скорости движения, в точке В груз переходит на участок ВС трубы, где на него действует кроме силы тяжести и силы трения (коэффициент трения f 2 = 0,2) переменная сила  , проекция которой на ось x Fx =–2sin (4p t) и сила Р = 4 t. Найти закон движения груза на участке ВС, т.е. x = f(t), где x = BD.
, проекция которой на ось x Fx =–2sin (4p t) и сила Р = 4 t. Найти закон движения груза на участке ВС, т.е. x = f(t), где x = BD.
 Решение:
Решение:






 1. Рассмотрим движение груза на участке АВ, считая его материальной точкой. Изображаем груз и действующие на него силы
1. Рассмотрим движение груза на участке АВ, считая его материальной точкой. Изображаем груз и действующие на него силы 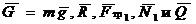 . Проводим оси A x 1 y 1 и составим дифференциальные уравнения движения точки в проекциях на эти оси:
. Проводим оси A x 1 y 1 и составим дифференциальные уравнения движения точки в проекциях на эти оси:

Рисунок 31. Расчетная схема
Далее находим:
 = G cos 45°,
= G cos 45°, 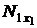 = 0,
= 0,  = – R = –2
= – R = –2 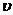 2,
2,  = – Q = –2,
= – Q = –2, 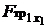 = –
= –  ,
,
 = - G sin 45°,
= - G sin 45°,  = N 1,
= N 1, 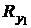 = 0,
= 0,  = 0,
= 0,  = 0.
= 0.
Кроме того, известно, что  = f 1 N 1, а
= f 1 N 1, а  = 0 (y 1 не изменяется). Из второго уравнения 0 = – G sin 45° + N 1 находим N 1 = G sin 45°, а значит
= 0 (y 1 не изменяется). Из второго уравнения 0 = – G sin 45° + N 1 находим N 1 = G sin 45°, а значит  = f 1 N 1 = f1G sin 45°, поэтому первое уравнение запишется:
= f 1 N 1 = f1G sin 45°, поэтому первое уравнение запишется:
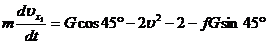 (8)
(8)
Учтя, что
 ,
,
разделив обе части (8) на m, имеем
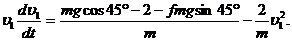
Подставляя числовые значения m = 2, g = 10, f = 0,1, получим:
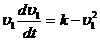 , где k = 5,37 м/с2.
, где k = 5,37 м/с2.
Разделяя переменные, запишем
 . (9)
. (9)
Интегрируя обе части уравнения (9) имеем:
 . (10)
. (10)
По начальным условиям при x 1 = 0 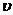 1 =
1 = 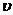 0, что даёт
0, что даёт  , и из
, и из
(10) находим 
Отсюда
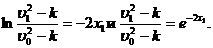
В результате находим
 . (11)
. (11)
Полагая в (11) x 1 = l = 2,5 и, заменяя k и 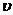 0 их значениями, определим скорость в точке В:
0 их значениями, определим скорость в точке В:
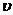 B = 5,37+(25–5,37)×(2,7) –5 = 5,5 (м/с).
B = 5,37+(25–5,37)×(2,7) –5 = 5,5 (м/с).
2. Рассмотрим движение груза на участке ВС. Проведём из точки В оси Вx и Вy и покажем действующие на него силы  . Составим уравнения движения груза в проекциях на оси x и y:
. Составим уравнения движения груза в проекциях на оси x и y:
 (12)
(12)
В уравнениях (12)  = f 2 N 2. Так как
= f 2 N 2. Так как  = 0, то из второго уравнения (12) имеем 0 = N 2 – mg cos 30°, откуда N 2 = mg cos 30°. Следовательно,
= 0, то из второго уравнения (12) имеем 0 = N 2 – mg cos 30°, откуда N 2 = mg cos 30°. Следовательно,  = f 2 mg cos 30°. Кроме того, Gx = G sin 30°= mg sin 30°, Fx = –2 sin (4 pt), Px = 4 t и первое уравнение (12) примет вид:
= f 2 mg cos 30°. Кроме того, Gx = G sin 30°= mg sin 30°, Fx = –2 sin (4 pt), Px = 4 t и первое уравнение (12) примет вид:
 . (13)
. (13)
Разделив обе части равенства на m и подставляя в (13) g = 10, f 2 = 0,2, получим:
 . (14)
. (14)
Умножая обе части (14) на dt и интегрируя, находим
 . (15)
. (15)
Будем отсчитывать время от момента, когда груз находился в точке В, считая в этот момент t = 0. Тогда при t = 0 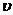 =
= 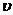 0 =
0 = 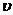 В = 5,5 м/с. Подставляя эти величины в (15), получим:
В = 5,5 м/с. Подставляя эти величины в (15), получим:
 ;
;
Поэтому  . (16)
. (16)
Но  , подставляя в (16), разделяя переменные и интегрируя, будем иметь
, подставляя в (16), разделяя переменные и интегрируя, будем иметь
 . (17)
. (17)
Так как при t = 0 x = 0, то С 3 = 0, а поэтому закон движения груза будет

где x – в метрах, t – в секундах.
Ответ: 
6 Задачи и вопросы для самоконтроля
1. Тело массой m= 50 кг, подвешенное на тросе, поднимается вертикально с ускорением а =0,5 м/с2. Определить силу натяжения троса (Ответ: 516 Н).
2. Определить модуль равнодействующей силы, действующей на материальную точку массой m =3 кг в момент времени t= 6 c, если она движется по оси Ох согласно уравнению х= 0,04 t3 (Ответ: 4,32 Н).
3. Материальная точка массой 1,4 кг движется прямолинейно по закону
х= 6 t2 +6 t +3. Определить модуль равнодействующей силы, приложенной к точке (Ответ: 16,8 Н).
4. Материальная точка массой 16 кг движется по окружности радиуса R =9 м со скоростью v =0,8 м/с. Определить проекцию равнодействующей силы, приложенной к точке, на главную нормаль к траектории (Ответ: 1,14 Н).
5. Материальная точка массой 1 кг движется по окружности радиуса r =2 м со скоростью v =2 t. Определить модуль равнодействующей сил приложенных к точке, в момент времени t =1 с (Ответ: 2,83 Н).
6. Тело движется вниз по гладкой плоскости, которая наклонена под углом a =25° к горизонту. Определить ускорение тела (Ответ: 4,15 м/с2).
7. Материальная точка массой m =5 кг движется под действием сил F1= 3 H и F2 =10 H (рисунок 32). Определить проекцию ускорения точки на ось Ох (Ответ: 1,13 м/с2).


Рисунок 32 Рисунок 33
8. Материальная точка М массой m движется по горизонтальной оси Ох под действием силы F =2 m (x +1) (рисунок 33). Определить ускорение точки в момент времени, когда ее координата х =0,5 м (Ответ: 3 м/с2).
9. Материальная точка массой m =900 кг движется по горизонтальной прямой под действием силы F =270 t, которая направлена по той же прямой. Определить скорость точки в момент времени t =10 с, если при t0 =0 скорость v0 =10 м/с (Ответ: 25 м/с).
10. Материальная точка массой 0,2 кг движется вдоль оси Ох под действием силы Fх = -0, 4 t. Определить скорость точки в момент времени t =2 с, если ее начальная скорость vхо =6 м/с (Ответ: 2 м/с).
11. Материальная точка массой  начала движение из состояния покоя по горизонтальной прямой под действием силы
начала движение из состояния покоя по горизонтальной прямой под действием силы  , которая направлена по той же прямой. Определить путь, пройденный точкой за
, которая направлена по той же прямой. Определить путь, пройденный точкой за 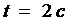 (Ответ: 0,8 м).
(Ответ: 0,8 м).
12. Тяжелое тело спускается по гладкой плоскости, наклоненной под углом 300 к горизонту. Найти, за какое время тело пройдет путь 9,6 м, если в начальный момент его скорость 2 м/с (Ответ: 1,6 с).
13. Материальная точка поднимается по шероховатый плоскости, составляющей угол  горизонтом, имея начальную скорость
горизонтом, имея начальную скорость  . Коэффициент трение
. Коэффициент трение  . Какой путь пройдет точка за время
. Какой путь пройдет точка за время  ? (Ответ: 62 м).
? (Ответ: 62 м).
14. Тело массой  находящееся на горизонтальной плоскости, приводится в движение из состояния покоя постоянной силой
находящееся на горизонтальной плоскости, приводится в движение из состояния покоя постоянной силой  . Какой путь пройдет тело за время
. Какой путь пройдет тело за время  , если коэффициент трения
, если коэффициент трения  ?
?
(Ответ: 18 м).
15. Как запишется основной закон динамики? (второй закон Ньютона).
16. Какой вид имеют дифференциальные уравнения движения свободной материальной точки в координатной форме?
17. В чем состоит первая задача динамики точки?
18. В чем состоит вторая задача динамики точки?
19. Как определяются значения произвольных постоянных, появляющихся при интегрировании дифференциальных уравнений движения материальной точки?
20. Какие уравнения динамики называются естественными уравнениями движения материальной точки?
Список литературы
1. Яблонский А.А., Никифорова В.М. Курс теоретической механики. Ч.1 М.: Высшая школа, 1984. - 343 с.
2. Тарг С.М. Краткий курс теоретической механики. М.: Наука, 1972. – 472 с.
3. Мещерский И.В. Сборник задач по теоретической механике. М.: Наука, 1981. - 480 с.
4. Бать С.М., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. Ч. 1 и 2. М.: Физматгиз, 1961. - 511, 663 с.
5. Сборник коротких задач по теоретической механике: Учеб. пособие для втузов / О.Э. Кеппе, Я.А. Виба, О.П. Грапис и др.; Под ред. О.Э. Кепе. М.: Высшая школа., 1989. - 368 с.
6. Ешуткин Д.Н., Григорчак В.С., Кожахметова А.К. и др. Теоретическая механика (задачи для самостоятельного изучения курса): Учеб. пособие. Караганда: КарГТУ, 2001. – 73 с.
7. Ешуткин Д.Н., Григорчак В.С., Смирнов Ю.М. Теоретическая механика: учеб. пособие. Караганда: КарГТУ, 2002 - 256 с.
8. Ешуткин Д.Н., Григорчак В.С., Кожахметова А.К. и др. Теоретическая механика: задания для самостоятельных работ: Учеб. пособие. Караганда: КарГТУ, 2002. – 115 с.