Необходимый теоретический материал

УДК 531.1

Иманбаева Л.Х., Орынтаева Г.Ж., Ганюков А.А., Безкоровайный П.Г. Методичекие указания для самостоятельной работы студентов с преподавателем, самостоятельной работы студентов, практическим занятиям и СРСП по теоретической механике на тему: «Плоское движение твердого тела К-4» / Под общ. ред. Л.Х. Иманбаевой Караганда:издательство КарГТУ, 2012.

Настоящее издание входят в состав серии методических указаний, которые охватывают основные разделы (статика, кинематика и динамика) курса теоретической механики. Они позволяют преподавателю выдавать индивидуальное задание каждому студенту из группы до тридцати человек. Все задания имеют одинаковую степень сложности. При относительно небольшом объеме каждое из них содержит необходимый теоретический материал по конкретной тематике, пример решения одного или двух вариантов задания, последовательность выполнения, цель работы, тестовые вопросы и задачи для самоконтроля. Тем самым обеспечивается единый порядок изложения каждой темы для всей серии методических пособий, что облегчает студентам ее усвоение за счет тренировки в одном и том же плане решения всех задач.

Рецензенты - член редакционно-издательского совета КарГТУ д-р техн. наук, проф. С.К. Тутанов

Утверждено редакционно-издательским советом университета

СОДЕРЖАНИЕ

4.1 Расчет многозвенного механизма

1. Цель и условия заданий.........................................................................................4

2. Исходные данные...................................................................................................4

3. Указания к выполнению......................................................................................10

4. Необходимый теоретический материал.............................................................10

5. Примеры выполнения..........................................................................................12

6. Задачи и вопросы для самоконтроля..................................................................21

Список литературы ……………………….……………......……………..............25

Расчет многозвенного механизма

Условия заданий

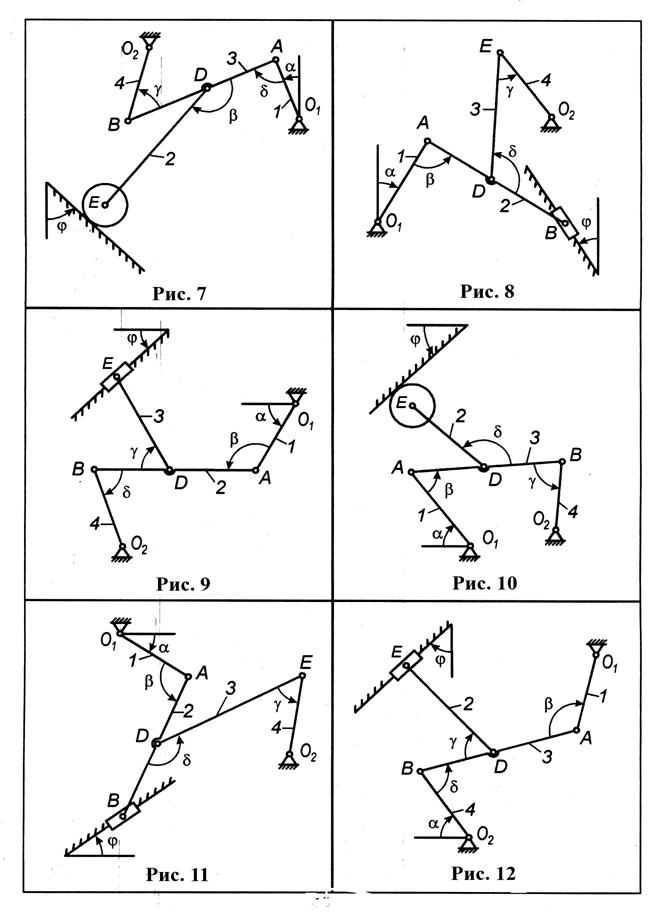
Положение механизма определяется углами a, b, γ, d, и j, приведенными в таблице. Промежуточные шарниры Д или В (рис. 6, 20) находятся в середине соответствующего стержня, качение диска (рис. 3, 7, 10, 14, 16, 17, 20, 24, 26, 28) происходит без проскальзывания. Заданную угловую скорость и угловое ускорение считать направленными против хода часовой стрелки.

Дуговые стрелки на рисунках показывают, как при построении чертежа механизма должны откладываться соответствующие углы: по ходу или против хода часовой стрелки. Построение чертежа следует начинать со стержня, положение которого определяется углом a. Длина стержней: l ₁= 1 м, l ₂= 3 м,

l ₃= 3,5 м, l ₄= 1,5 м.

Определить величины, указанные в таблице в столбцах «Найти».

Исходные данные и расчетные схемы

Исходные данные

Вариант	Углы, градусы	Дано	Найти
a	b	γ	d	j	w₁, с^-1	e₁, с^-2	u точек	w звена	точек	e звена
								Д, Е	АВ	В	АВ
								В, Е	ДЕ	В	АВ
								В, Е	ДЕ	В	АВ
								В, Е	АВ	В	АВ
								Д, Е	АВ	В	АВ
								В, Е	ДЕ	В	АВ
								Д, Е	АВ	В	АВ
								В, Е	АВ	В	АВ
								В, Е	ДЕ	В	АВ
								В, Е	ДЕ	В	АВ

Указания к выполнению

Механизм и движение, которое исследуется, надо изобразить на рисунке в том положении, для которого требуется определить соответствующие кинематические характеристики. При решении задач плоского многозвенного механизма рекомендуется придерживаться нижеследующего порядка.

1. Установить число тел (звеньев), входящих в данный механизм, и определить вид движения каждого из них.

2. Рассмотреть тело, движение которого задано (ведущее звено), и определить для него все величины, указанные в условии задачи, затем найти скорость точки, соединяющей это тело с последующим.

3. Определить для последующего тела, имеющего общую точку с первым телом, положение МЦС, мгновенную угловую скорость тела, и скорость точки, указанной в таблице.

4. Рассматривая последовательно все тела данного механизма, сначала определяются мгновенные угловые скорости и скорости точек тел, указанных в таблице.

5. Придерживаясь этого порядка, аналогичным образом определяются мгновенные угловые ускорения и ускорения точек тел, указанных в таблице.

Необходимый теоретический материал

Плоским (или плоскопараллельным) движением называется такое движение твердого тела, при котором все его точки движутся в плоскостях, параллельных некоторой неподвижной плоскости. Для изучения плоского движения твердого тела достаточно исследовать движение плоской фигуры, являющейся сечением твердого тела плоскостью, параллельной неподвижной.

Всякое перемещение плоской фигуры можно разложить на два движения: поступательное вместе с некоторой точкой, принятой за полюс, и вращение тела вокруг оси, проходящей через этот полюс, перпендикулярной плоскости движения. Причем характеристики поступательного движения зависят от выбора полюса, а вращательное движение не зависит от выбора полюса. Уравнениями движения плоской фигуры в неподвижной системе координат будут:

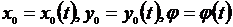, где - координаты полюса, - угол поворота подвижных осей относительно неподвижных.

Скорость любой точки плоской фигуры равна векторной сумме скорости полюса и скорости этой точки во вращении вокруг оси, проходящей через полюс (рис. 31)

, где - скорость полюса О; а - скорость точки А во вращении вокруг полюса, причем

а .

Теорема о проекциях скоростей двух точек: проекции скоростей двух точек на прямую, соединяющую эти точки, равны между собой, т.е. 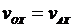(рис. 31), или

При непоступательном движении плоской фигуры в каждый момент времени существует точка тела, как бы т.е. неразрывно связанная с ним, скорость которой равна нулю. Эта точка называется мгновенным центром скоростей (МЦС). Выбирая эту точку Р за полюсе получим:

, причем .

Ускорение любых двух точек плоской фигуры А и В связаны между собой следующим соотношением (рис. 32)

причем

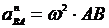, вектор направлен от В к А

вектор направлен в соответствии с направлением углового ускорения плоской фигуры.

Необходимый теоретический материал

Поиск по сайту