Практическая работа №4
Название работы: Построение сопряжений двух прямых дугой окружности заданного радиуса,дуг с дугами и дуги с прямой.
Цель работы: - изучение методов построения сопряжений,приобретение навыков ввыполнении геометрических построений, продолжение закрепления навыков работы с чертежными инструментами и оформления чертежа;
- способствование развитию пространственного воображения, логического
мышления.
Основные понятия: (при необходимости)
Исходные данные (задание): Выполнить примеры построения сопряжений и нанести размеры.
Задание выполняется в одном варианте. Масштаб 1:1.
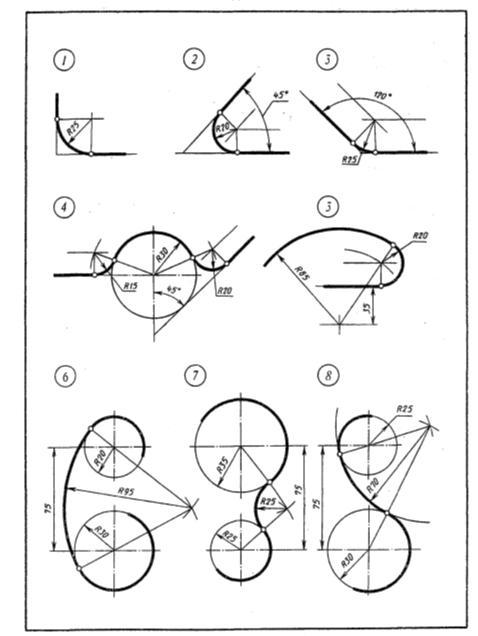
Порядок выполнения:
Методические указания по выполнению работы.
При выполнении чертежа рекомендуется соблюдать следующую последовательность:
1. Подготовить формат листа А-4, начертить внешнюю и внутреннюю рамки чертежа, отвести место для основной надписи и дополнительной графы.
Масштаб изображения М 1:1
2. Провести осевые и центровые линии, взяв расстояние между ними согласно размерам детали и учитывая равномерность распределения изображений на поле чертежа.
3. Провести дуги окружностей, окружности и прямые линии, положение которых определено заданными размерами и не требует дополнительных построений.
4. Выполнить геометрические построения и сопряжения. Предварительные построения выполнять тонкими линиями твердым карандашом (Т или 2Т).
5. Нанести выносные и размерные линии, надписать размерные числа (шрифт 5).
6. Проверить правильность выполнения чертежа и обвести чертеж карандашом (ТМ или М). Вначале обвести дугу окружностей и окружности, затем – прямые линии. Обвести внутреннюю рамку чертежа. Все построения сопряжений сохранить.
Краткие сведения из теории.
При выполнении чертежей деталей встречаются случаи плавного перехода от одной линии к другой, называемые сопряжениями. Различают виды сопряжений:
a) Сопряжение двух прямых дугой окружности заданного радиуса;
b) Сопряжение дуги окружности и прямой линии дугой заданного радиуса
c) Сопряжение углов дугой заданного радиуса;
Сопряжение двух окружностей дугой заданного радиуса. Различают внешнее, внутреннее и смешанное касания.
Если одна окружность с центром О касается окружности с центром О1 с внешней стороны, то такое сопряжение называется внешним. При этом точка сопряжения В лежит на линии центров О и О1, а расстояние между центрами О и О1 равно сумме радиусов R + r (рис. 1а).
Если одна окружность касается другой окружности внутри, то такое сопряжение называется внутренним, при этом точка сопряжения В лежит на линии центров ОО1 = R – r (рис. 1в).
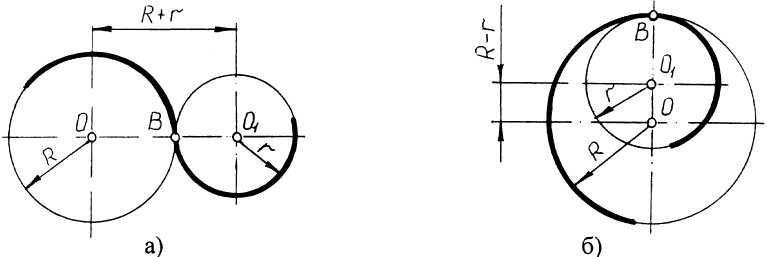
Рис.1 Внешнее и внутреннее сопряжения
Чтобы построить сопряжение необходимо найти:
1. Центр сопряжения
2. Точки сопряжения
Прежде чем начертить, необходимо провести анализ графического состава изображения, чтобы установить, какие геометрические построения необходимо применить.
Сопряжение двух прямых линий (скругление углов)
Здесь возможны три случая: прямые пересекаются под прямым углом друг к другу (рис.2,а), прямые пересекаются под острым углом и прямые пересекаются под тупым углом (рис.2,б,в,). Во всех трех случаях методика решения одна и та же.
Параллельно сторонам угла, образованного данными прямыми, провести прямые на расстоянии заданного радиуса R. Точка пересечения этих прямых является центром О сопряжения. Из центра опустить перпендикуляры к сторонам данного угла и определить точки сопряжения А. Между точками А из центра О провести сопрягающую дугу радиуса R.
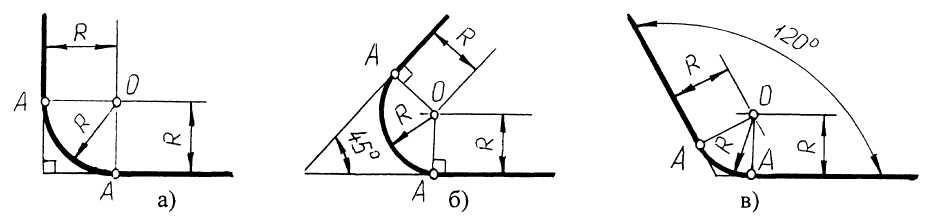
Рис.2 Построение сопряжения двух прямых линий Сопряжение дуги окружности и прямой линии второй дугой
Если прямая не пересекает окружность, то можно осуществить внешнее сопряжение (рис.3, а) и внутреннее сопряжение (рис.3, б).
В первом случае необходимо провести вспомогательную прямую, параллельную заданной прямой, на расстоянии заданного радиуса R1 и из точки О вспомогательную окружность радиуса (R + R1). Пересечение вспомогательных линий даст центр дуги сопряжения О1.
Опуская из точки О1 перпендикуляр на заданную прямую, найти точку сопряжения А, а соединяя точку О1 с О, найти точку сопряжения на заданной окружности А1.
Во втором случае построение аналогично предыдущему случаю, но так как сопряжение внутреннее, то вспомогательную окружность проводят радиусом R1 – R (рис.13, б).
Построение сопряжения прямой с окружностью радиуса R, когда прямая пересекает окружность (рис.3, в), аналогично предыдущему, то есть необходимо провести вспомогательную прямую параллельно заданной прямой на расстоянии радиуса R1 и вспомогательную окружность радиусом R - R1. Затем найти точки сопряжения А и А1.
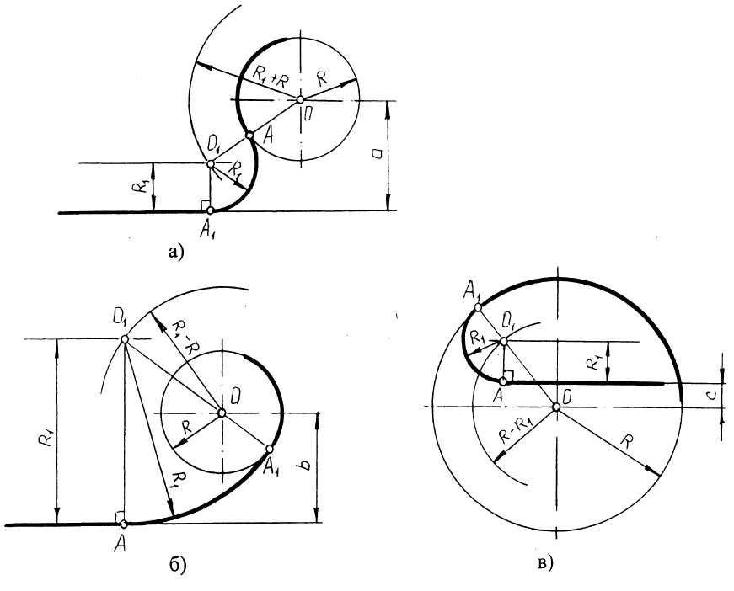
Рис.3. Сопряжение дуги окружности и прямой линии второй дугой
Сопряжение двух дуг окружностей третьей дугой
В данном случае сопрягающая дуга радиуса R может касаться заданных дуг радиусов R1
и R2 с внешней стороны (рис.4, а), создавать внутреннее касание (рис.4, б) или сочетание внешнего и внутреннего касания (рис.4, в, г).
При построении внешнего сопряжения центр О искомой дуги радиуса R находится на пересечении вспомогательных окружностей, проведенных из центров О1 и О2 соответствующими радиусами R + R1 и R + R2. Соединяя О1 и О2 с О, необходимо найти точки сопряжения А1 и А2. Между точками А1 и А2 из центра О провести сопрягающую дугу радиуса R (рис.4, а).
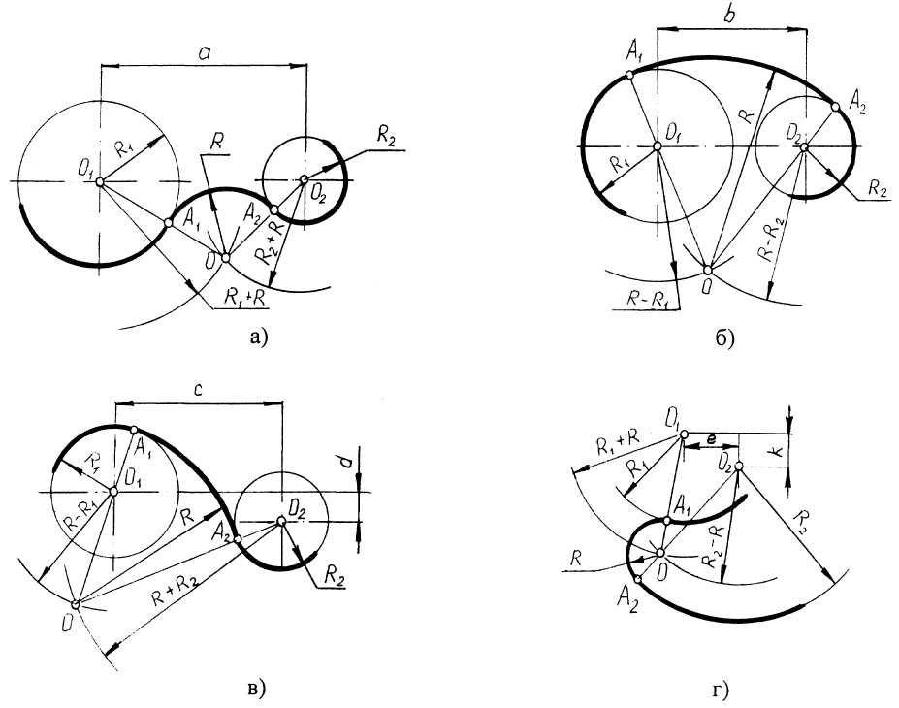
Рис.4. Построение сопряжения двух дуг окружностей третьей дугой
Построение внутреннего касания аналогично, только вспомогательные окружности проводят радиусами R - R1 и R - R2 (рис.4, б).
При построении смешанного касания (сочетание внутреннего и внешнего) центр сопряжения находится на пересечении вспомогательных окружностей радиусами R- R1 и R + R2 (рис.4, в, г). Затем необходимо найти точки сопряжения А1, А2 и соединить их сопрягающей дугой.
Нанесение размеров
Величины изображенного изделия и его элементов на чертежах определяются размерами, общее число которых должно быть минимальным, но достаточным для его изготовления и контроля. Линейные размеры указывают в миллиметрах без обозначения единиц. Угловые единицы указывают на чертеже в градусах (°). Правила нанесения размеров установлены ГОСТ 2.307-68*. Размеры на чертежах указывают размерными линиями. Размерные линии ограничивают стрелками (рис.16, а), которые острием касаются выносных линий, линий контура, осевых линий. Выносная линия выступает за стрелку на 1–2 мм. Размерную линию проводят параллельно отрезку, размер которого указывают, по возможности, вне контура изображения (рис.16, б). Расстояние от размерной линии до контура и между параллельными размерными линиями должно быть 10 мм. Размерные линии не должны быть продолжением линий контура, осевых, центровых и выносных линий. Все перечисленные линии не могут быть использованы в качестве размерных. Размерные линии не должны
пересекаться с выносными, поэтому меньшие размеры наносят ближе к линиям контура, а большие дальше. Форму стрелки и ее размеры выдерживают на чертеже одинаковыми. Каждый размер указывается только один раз. Размерные числа наносят над размерной линией возможно ближе к ее середине.
Для обозначения диаметра перед размерным числом наносят знак Ф, для обозначения радиуса – R (рис.16, в), размеров квадратных элементов - □. Размерную линию при указании величины углов проводят в виде дуги с центром в вершине угла.
Перечень оборудования: (ТСО, наглядные пособия): Плакаты.
Вопросы для повторения:
1. Что такое сопряжение?
5. Как определить точку касания при построении окружности, касательной к прямой?
6. На чем основан общий прием нахождения центра сопрягающей дуги?
7. Как выполняется сопряжение двух заданных окружностей дугой заданного радиуса?
8. Как выполняется сопряжение двух пересекающихся прямых?
Литература: 1.С.К.Боголюбов,Черчение. –М.:Машиностроение, 1989стр.35-39
2. Куликов В.П. Стандарты инженерной графики. Учебное пособие. Стр.41-44
3. С.К. Боголюбов, Индивидуальные задания по курсу черчения: Практ. пособие для учащихся техникумов, стр. 19 (30 вариантов заданий).
4. О.М. Букова, Е.В. Ларионова. Техника черчения. Геометрические построения. Авторская педагогическая разработка, Иркутск, 2013. – 24с.:ил