Методом случайной повторной выборки было взято для проверки на вес 200 шт. деталей. В результате проверки был установлен средний вес детали (30г) при среднем квадратическом отклонении 4 г. С вероятностью 0,954 требуется определить предел, в котором находится средний вес деталей в генеральной совокупности.
Надежность результатов выборки проверяется расчетами ошибок: средней ошибки выборки и предельной ошибки выборки.
Средняя ошибка (m) зависит от способа отбора (повторного или бесповоротного) и рассчитывается:
при бесповторном отборе при повторном отборе
m 
m 
где n – численность выборки;
N – численность генеральной совокупности;
σ 2 - дисперсия выборочной совокупности.
Предельная ошибка выборки (D) рассчитывается по формуле
D 
где t – коэффициент доверия, зависит от значения вероятности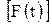 
при 
= 0,997 t = 3; при = 0,988 t = 2,5;
при = 0,954 t = 2; при = 0,866 t = 1,5;
при = 0,683 t = 1; при = 0,383 t = 0,5.
В типовой задаче задано s = 4, следовательно, s 2 = 16. Тогда
при повторном отборе m 
Предельная ошибка выборочной средней с вероятностью = 0,954
t = 2 составит D = 2*0,28 = 0,56 (г)
Верхняя граница среднего веса в генеральной совокупности будет равна
30 + 0,56 = 30,56
Нижняя граница - 30 – 0,56 = 29,44 (г).
С вероятностью 0,954 можно утверждать, что средний вес детали колеблется в пределах
29,44 £ 
Задание 5 на самостоятельную работу
Вариант 1
Для определения средней длины деталей необходимо провести выборочное обследование методом случайного повторного отбора. Какое количество деталей нужно отобрать, чтобы ошибка выборки не превышала 2 мм с вероятностью 0,954 при квадратическом отклонении 8 мм?
Вариант 2
В порядке случайного бесповоротного контроля веса изделий были получены: величина дисперсии признака, равная 20 г, и средний вес изделия, равный 16 г. Определить вероятность того, что средняя по всей партии изделий отличается от выборочной средней не более чем на 0,5 г. Вся партия изделий равна 10000 шт., контролю подвергнуто 500 шт.
|
|
Вариант 3
При определении средней продолжительности поездки на работу проводится 10 % выборка работающего населения. Численность работающего населения города – 17400 чел. Средняя продолжительность поездки – 43 минуты, при среднем квадратическом отклонении 16 минут. Определить с вероятностью 0,997 среднюю продолжительность поездки работающего населения города.
Вариант 4
Для определения зольности угля месторождения в порядке случайной повторной выборки взято 370 проб. В результате лабораторных исследований установлена средняя зольность угля в выборке 17 % с дисперсией выборки 6 %. С вероятностью 0,997 определить пределы, в которых находится средняя зольность угля месторождения.
Вариант 5
Какое число студентов нужно отобрать в порядке бесповторного случайного отбора для определения их среднего возраста из 4000 студентов высшего учебного заведения, чтобы предельная ошибка с вероятностью 0,954 не превышала 0,5 года. Известно, что среднее квадратическое отклонение возраста студента составляет 1,5 года.