Электрический ток, условия его существования, характеристики. Законы Ома и Джоуля-Ленца в интегральной и дифференциальной форме. Обобщенный закон Ома. Правила Кирхгофа. Расчет разветвленных цепей. Элементарная классическая теория электропроводности металлов.
| 3 Основные формулы | |
| Средняя скорость материальной точки | |
| в векторном виде: | 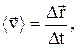
|
в скалярном виде:
где  – радиус-вектор точки; – радиус-вектор точки;  – вектор перемещения точки за промежуток времени – вектор перемещения точки за промежуток времени  ; ;  – путь, пройденный точкой за промежуток времени – путь, пройденный точкой за промежуток времени  . .
| 
|
| Мгновенная скорость материальной точки | |
| в векторном виде: | 
|
| в скалярном виде: | 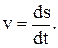
|
| Среднее ускорение материальной точки: | 
|
| Мгновенное ускорение материальной точки: | 
|
| Полное ускорение при криволинейном движении | |
| в векторном виде: | 
|
| в скалярном виде: | 
|
| Тангенциальное ускорение: | 
|
| Нормальное ускорение: где R – радиус кривизны траектории в данной точке. | 
|
Путь и скорость для равнопеременного прямолинейного движения:
где  – начальная скорость. – начальная скорость.
| 

|
| Угловая скорость в векторном виде: | 
|
в скалярном виде:
где  –угловое перемещение. –угловое перемещение.
| 
|
| Угловое ускорение в векторном виде: | 
|
| в скалярном виде: | 
|
Связь угловой скорости с периодом и частотой вращения:
где Т – период,  – частота вращения, N – число оборотов, совершаемых телом за время t. – частота вращения, N – число оборотов, совершаемых телом за время t.
| 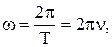
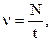
|
Угловое перемещение и угловая скорость для равнопеременного вращательного движения:
где 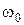 – начальная скорость. – начальная скорость.
| 
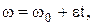
|
| Связь между линейными и угловыми величинами: где R – радиус кривизны траектории. |  , ,  , ,

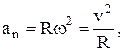
|
| Уравнение динамики поступательного движения материальной точки (II закон Ньютона): | 
|
| или | 
|
где  – геометрическая сумма сил, действующих на материальную точку; m – масса, – геометрическая сумма сил, действующих на материальную точку; m – масса,  – ускорение, – ускорение,  – импульс точки. – импульс точки.
| |
Сила тяжести:
где  – ускорение свободного падения. – ускорение свободного падения.
| 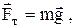
|
| Сила гравитационного взаимодействия: где G – гравитационная постоянная, m1 и m2 – массы взаимодействующих тел, находящихся на расстоянии R друг от друга. | 
|
| Сила упругости: где k – коэффициент упругой силы (коэффициент жесткости – в случае пружины); х – абсолютная деформация. | 
|
Сила трения скольжения:
где  – коэффициент трения скольжения; N – сила нормального давления. – коэффициент трения скольжения; N – сила нормального давления.
| 
|
Момент силы относительно оси вращения:
(При условии, что сила  , действующая на тело, лежит в плоскости перпендикулярной оси вращения). Здесь L – плечо силы , действующая на тело, лежит в плоскости перпендикулярной оси вращения). Здесь L – плечо силы  (кратчайшее расстояние от оси вращения до линии действия силы). (кратчайшее расстояние от оси вращения до линии действия силы).
|  . .
|
| Момент инерции относительно оси вращения | |
| материальной точки: где m – масса точки; r – расстояние от оси вращения; |  , ,
|
системы материальных точек:
где  – масса i-й точки; – масса i-й точки;  – расстояние этой точки от оси вращения; n – общее число материальных точек системы; – расстояние этой точки от оси вращения; n – общее число материальных точек системы;
| 
|
| твердого тела: | 
|
|
|
Таблица 1 – Моменты инерции некоторых тел правильной геометрической формы
| Тело | Ось, относительно которой определяется момент инерции | Момент инерции |
| Однородный тонкий стержень массой m и длиной l | Проходит перпендикулярно стержню через его центр масс | 
|
| Однородный тонкий стержень массой m и длиной l | Проходит перпендикулярно стержню через его конец |  
|
| Тонкое кольцо, обруч, труба радиусом R и массой m, равномерно распределенной по ободу | Проходит перпендикулярно плоскости основания через центр масс |

|
| Круглый однородный диск (цилиндр) радиусом R и массой m | Проходит перпендикулярно плоскости основания через центр масс | 
|
| Однородный шар массой m и радиусом R | Проходит через геометрический центр | 
|
|
|
Момент импульса  тела, вращающегося относительно неподвижной оси:
где J – момент инерции тела относительно этой же оси вращения, тела, вращающегося относительно неподвижной оси:
где J – момент инерции тела относительно этой же оси вращения, 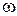 – угловая скорость. – угловая скорость.
|
 , ,
|
| Уравнение динамики вращательного движения твердого тела относительно неподвижной оси: | 
|
Если момент инерции тела не изменяется с течением времени, то уравнение динамики вращательного движения принимает вид:
где  – угловое ускорение. – угловое ускорение.
|
 , ,
|
| Закон сохранения импульса для замкнутой системы: где n – число материальных точек (тел), входящих в систему. | 
|
| Закон сохранения момента импульса для замкнутой системы: | 
|
Элементарная работа силы:
где  – проекция силы – проекция силы  на направление перемещения на направление перемещения  , ,  – угол между направлениями силы и перемещения. – угол между направлениями силы и перемещения.
| 
|
| Работа, совершаемая переменной силой, на пути S: | 
|
| Мгновенная мощность: |  ; ;
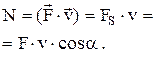
|
| Кинетическая энергия поступательного движения тела массы m: | 
|
| Кинетическая энергия вращательного движения тела, имеющего момент инерции J, вокруг неподвижной оси: |

|
Кинетическая энергия катящегося тела:
где  – скорость центра масс, – скорость центра масс, 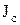 – момент инерции, относительно оси, проходящей через центр масс тела. – момент инерции, относительно оси, проходящей через центр масс тела.
| 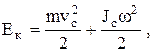
|
| Потенциальная энергия тела, поднятого над поверхностью Земли на высоту h: где g – ускорение свободного падения. |
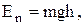
|
| Потенциальная энергия упруго деформированного тела: где k – коэффициент упругой силы; х – абсолютная деформация. | 
|
Уравнение гармонических колебаний:
где x – смещение колеблющейся точки от положения равновесия; t – время;  – соответственно, амплитуда, круговая (циклическая) частота, начальная фаза колебаний; – соответственно, амплитуда, круговая (циклическая) частота, начальная фаза колебаний;  – фаза колебаний в момент времени t. – фаза колебаний в момент времени t.
| 
|
Круговая (циклическая) частота колебаний:
где  и T – частота и период колебаний. и T – частота и период колебаний.
|  , ,
 , ,
|
| Скорость точки, совершающей гармонические колебания: | 
|
| Ускорение точки, совершающей гармонические колебания: | 
|
| Энергия материальной точки, совершающей гармонические колебания: | |
– кинетическая:

| |
– потенциальная:

| |
– полная:

| |
| где m – масса точки, k – коэффициент упругой (квазиупругой) силы. | |
| Период колебаний тела, подвешенного на пружине (пружинный маятник): где m – масса тела, k – коэффициент жесткости пружины. | 
|
Период колебаний математического маятника:
где  – длина маятника; g – ускорение свободного падения. – длина маятника; g – ускорение свободного падения.
| 
|
Период колебаний физического маятника:
где J – момент инерции колеблющегося тела относительно оси колебаний, а – расстояние центра масс маятника от оси колебаний;  – приведенная длина физического маятника. – приведенная длина физического маятника.
| 
|
Количество вещества тела (системы):
где N – число структурных элементов (молекул, атомов, ионов и т.п.), составляющих тело (систему); 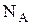 – постоянная Авогадро. – постоянная Авогадро.
| 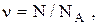
|
Молярная масса вещества:
где m – масса однородного тела (системы); 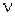 – количество вещества этого тела. – количество вещества этого тела.
| 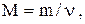
|
Молярная масса смеси газов:
где  – масса i-го компонента смеси; – масса i-го компонента смеси;  – количество вещества i -го компонента смеси; k – число компонентов смеси. – количество вещества i -го компонента смеси; k – число компонентов смеси.
| 
|
Уравнение состояния идеальных газов (уравнение Менделеева - Клапейрона):
где m – масса газа; М – его молярная масса; R – молярная газовая постоянная; Т – термодинамическая температура; 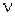 – количество вещества. – количество вещества.
|  или
или

|
Закон Дальтона:
где р – давление смеси газов;  – парциальное давление i-го компонента смеси, k – число компонентов смеси. – парциальное давление i-го компонента смеси, k – число компонентов смеси.
| 
|
| Концентрация частиц (молекул, атомов и т.п.) однородной системы: где N – число частиц, V – объем системы. | n=N/V, |
Основное уравнение молекулярно - кинетической теории газов:
где р – давление газа, n – концентрация молекул,
 – средняя кинетическая энергия поступательного движения молекулы. – средняя кинетическая энергия поступательного движения молекулы.
|

|
| Средняя кинетическая энергия, приходящаяся на одну степень свободы молекулы: | 
|
| приходящаяся на все степени свободы молекулы (полная энергия молекулы): | 
|
| где k – постоянная Больцмана; Т – термодинамическая температура; i – число степеней свободы молекулы. Для одноатомной молекулы – i=3, для двухатомной – i=5, для молекул, состоящих из трех и более атомов, – i=6. | |
| Зависимость давления газа от концентрации молекул и температуры: | p=nkT. |
| Скорости молекул газа: | |
| – среднеквадратичная: | 
|
| – средняя арифметическая: | 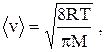
|
| – наиболее вероятная: | 
|
Внутренняя энергия идеального газа:
где  – количество вещества; m – масса газа; М – молярная масса газа; R – молярная газовая постоянная. – количество вещества; m – масса газа; М – молярная масса газа; R – молярная газовая постоянная.
| 
|
Первое начало термодинамики:
где Q – количество теплоты, полученное системой;  – изменение внутренней энергии системы; А – работа, совершенная системой против внешних сил. – изменение внутренней энергии системы; А – работа, совершенная системой против внешних сил.
| 
|
| Первое начало термодинамики для бесконечно малого изменения состояния системы: |

|
| Связь между молярной (Сm ) и удельной (с) теплоемкостями газа: где М – молярная масса газа. | Сm = сМ, |
| Молярные теплоемкости газа | |
| при постоянном объеме: | 
|
| при постоянном давлении: | 
|
| Уравнение Майера: где R – молярная газовая постоянная. | СP = CV +R, |
| Показатель адиабаты: | 
|
Уравнение адиабатного процесса (уравнение Пуассона):
где  – показатель адиабаты. – показатель адиабаты.
| 


|
| Количество теплоты, полученное системой или отданное ею, | |
| при изохорном процессе: | 

|
| при изобарном процессе: | 

|
где  и и 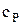 – удельные теплоемкости при постоянном объеме и давлении, а – удельные теплоемкости при постоянном объеме и давлении, а  и и  – соответствующие молярные теплоемкости, – соответствующие молярные теплоемкости,  – количество вещества. – количество вещества.
| |
| Изменение внутренней энергии идеального газа: | 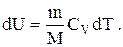
|
| Элементарная работа, совершаемая газом при изменении его объема: |

|
| Полная работа газа при изменении объема: где V1 и V2 – соответственно начальный и конечный объемы газа. | 
|
| Работа газа при изобарном процессе: |
 
|
| при изотермическом процессе: |  
|
| при адиабатном процессе: где Т1, Т2 и V1, V2 – соответственно, начальные и конечные температуры и объемы газа. | 
|
| Коэффициент полезного действия тепловой машины: где Q1 – количество теплоты, полученное от нагревателя, Q2 – количество теплоты, отданное холодильнику. | 
|
| Максимальный коэффициент полезного действия тепловой машины (КПД цикла Карно): где Т1 и Т2 – температуры нагревателя и холодильника, соответственно. | 
|
| Изменение энтропии системы при переходе из состояния 1 в состояние 2: | 
|
Сила взаимодействия точечных зарядов (закон Кулона):
где F – сила взаимодействия двух точечных зарядов  и и  , направленная вдоль прямой, соединяющей их центры; r – расстояние между зарядами; , направленная вдоль прямой, соединяющей их центры; r – расстояние между зарядами;  – диэлектрическая проницаемость среды; – диэлектрическая проницаемость среды;  – электрическая постоянная. – электрическая постоянная.
|  , ,
|
| Вектор напряженности электрического поля: |  . .
|
| Напряженность электрического поля, создаваемого точечным зарядом q на расстоянии r от заряда: | 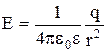 . .
|
| Напряженность электрического поля, создаваемого металлической сферой радиусом R с общим зарядом q, на расстоянии r от центра сферы: | |
| а) внутри сферы (r<R): | Е=0; |
| б) на поверхности сферы (r=R): |  ; ;
|
| в) вне сферы (r>R): |  . .
|
Напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром), на расстоянии r от ее (его) оси:
где  – линейная плотность заряда. – линейная плотность заряда.
|
 , ,
|
Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью:
где  – поверхностная плотность заряда. – поверхностная плотность заряда.
|  , ,
|
Напряженность поля в пространстве между двумя параллельными бесконечными равномерно и разноименно заряженными плоскостямис одинаковой по величине поверхностной плотностью заряда  : :
|
 . .
|
Потенциал электрического поля:
где  – потенциальная энергия точечного заряда q0, помещенного в данную точку поля. – потенциальная энергия точечного заряда q0, помещенного в данную точку поля.
| 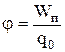 , ,
|
| Потенциал электрического поля, создаваемого точечным зарядом q на расстоянии r от заряда: |  . .
|
| Потенциал электрического поля, создаваемого металлической сферой радиусом R с общим зарядом q, на расстоянии r от центра сферы: | |
| а) внутри сферы (r<R): |  ; ;
|
| б) на поверхности сферы (r=R): |  ; ;
|
| в)вне сферы (r>R): |  . .
|
| Связь потенциала с напряженностью электрического поля: |  . .
|
| Вектор электрического смещения: |  . .
|
Поток вектора  через поверхность S:
где Еn – проекция вектора через поверхность S:
где Еn – проекция вектора  на направление нормали к элементарной площадке dS. на направление нормали к элементарной площадке dS.
| 
 , ,
|
Если поле однородно, поверхность S – плоская, то:
где  – угол между вектором – угол между вектором  и нормалью к поверхности S. и нормалью к поверхности S.
|  , ,
|
Теорема Остроградского-Гаусса:
где 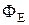 – поток вектора напряженности – поток вектора напряженности  через произвольную замкнутую поверхность S, охватывающую заряды q1, q2, …qn. через произвольную замкнутую поверхность S, охватывающую заряды q1, q2, …qn.
|  , ,
|
Работа, совершаемая электрическим полем при перемещении точечного заряда q из одной точки поля, имеющей потенциал  , в другую, имеющую потенциал , в другую, имеющую потенциал  : :
| А=q( - -  )= = )= =  . .
|
Электрическая емкость уединенного проводника:
где q – заряд проводника,  – его потенциал. – его потенциал.
|  , ,
|
Электрическая емкость конденсатора:
где q – заряд конденсатора,  – разность потенциалов между обкладками конденсатора. – разность потенциалов между обкладками конденсатора.
|  , ,
|
Электрическая емкость уединенной проводящей сферырадиусом R, находящейся в бесконечной среде с диэлектрической проницаемостью  : :
|
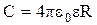 . .
|
Электрическая емкость плоского конденсатора:
где S – площадь каждой из обкладок конденсатора;
d – расстояние между обкладками;  – диэлектрическая проницаемость диэлектрика, заполняющего пространство между обкладками. – диэлектрическая проницаемость диэлектрика, заполняющего пространство между обкладками.
|  , ,
|
Электрическая емкость плоского слоистого конденсатора:
где di – толщина i-го слоя диэлектрика, 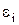 – его диэлектрическая проницаемость. – его диэлектрическая проницаемость.
|  , ,
|
| Электроемкость батареи конденсаторов, соединенных: – последовательно: |  ; ;
|
| – параллельно: где Сi – емкость i-го конденсатора, N – число конденсаторов. |  , ,
|
Энергия электрического поля заряженного проводника:
где q – заряд,  – потенциал, С – электрическая емкость проводника. – потенциал, С – электрическая емкость проводника.
| 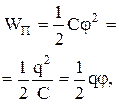
|
| Энергия электрического поля заряженного конденсатора: где С – электрическая емкость конденсатора; U – разность потенциалов на его обкладках. | 
|
Объемная плотность энергии электрического поля:
где Е – напряженность электрического поля в среде с диэлектрической проницаемостью  ; D – электрическое смещение. ; D – электрическое смещение.
| 
|
| Сила тока: |  . .
|
| Плотность тока: |  . .
|
Сопротивление однородного проводника:
где  – удельное сопротивление, – удельное сопротивление,  – длина, S – площадь поперечного сечения проводника. – длина, S – площадь поперечного сечения проводника.
|  , ,
|
| Сопротивление при последовательном и параллельном соединении проводников: где Ri – сопротивление i –го проводника, N – число проводников. |  , ,  , ,
|
Закон Ома в дифференциальной форме:
где  – удельная электрическая проводимость, – удельная электрическая проводимость,  – напряженность электрического поля. – напряженность электрического поля.
|  , ,
|
| Закон Ома для однородного участка цепи: где I – сила тока, текущего по однородному проводнику, U – напряжение на его концах, R – электрическое сопротивление проводника. |  , ,
|
Закон Ома для неоднородного участка цепи в интегральной форме:
где  – суммарная ЭДС на данном участке,
R – суммарное сопротивление внешней цепи,
r – внутреннее сопротивление источника ЭДС. – суммарная ЭДС на данном участке,
R – суммарное сопротивление внешней цепи,
r – внутреннее сопротивление источника ЭДС.
| 
|
| Закон Ома для замкнутой цепи: |  . .
|
Закон Джоуля-Ленцав дифференциальной форме:
где w – тепловая мощность тока,  – удельная электрическая проводимость, – удельная электрическая проводимость,  – напряженность электрического поля. – напряженность электрического поля.
|  , ,
|
| Закон Джоуля– Ленцав интегральной форме: где dQ – количество теплоты, выделяющейся в неподвижном и химически не изменяющемся проводнике при протекании через него тока силой I в течение времени dt. | 
|
| Мощность в цепи постоянного тока: | |
| – полная (выделяющаяся во всей замкнутой цепи): | 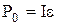 , ,
|
| – полезная (выделяющаяся на внешнем сопротивлении R): | 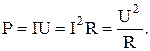
|
| К.П.Д. источника тока: | 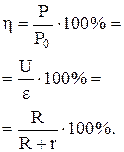
|
| Правила Кирхгофа Первое. Алгебраическая сумма сил токов, сходящихся в узле, равна нулю: |

|
Второе. В любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов  на сопротивления на сопротивления 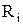 соответствующих участков этого контура равна алгебраической сумме ЭДС соответствующих участков этого контура равна алгебраической сумме ЭДС  , встречающихся в этом контуре:.. , встречающихся в этом контуре:..
| 
|
|
|
Примеры решения задач
 Пример 1. Кинематическое уравнение движения материальной точки по прямой имеет вид
Пример 1. Кинематическое уравнение движения материальной точки по прямой имеет вид  , где
, где  ,
,  ,
,  . Для момента времени
. Для момента времени  определить: 1) координату
определить: 1) координату  точки; 2) мгновенную скорость
точки; 2) мгновенную скорость  ; 3) мгновенное ускорение
; 3) мгновенное ускорение  ; 4) среднюю скорость за промежуток времени с момента начала движения до
; 4) среднюю скорость за промежуток времени с момента начала движения до  .
.

 Решение
Решение
1–Координату точки, для которой известно кинематическое уравнение движения, найдем, подставив в уравнение движения заданное значение времени  :
:
 .
.
Подставив в это выражение значения постоянных А, В, С, и  , произведем вычисления:
, произведем вычисления:  .
.
2–Уравнение, описывающее зависимость скорости от времени, найдем, продифференцировав координату  по времени:
по времени:
 .
.
Тогда в заданный момент времени  мгновенная скорость
мгновенная скорость 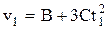 .
.
Подставим сюда значения В, С,  и произведем вычисления:
и произведем вычисления:  .
.
Знак минус в полученном значении скорости указывает на то, что в данный момент времени скорость материальной точки направлена в сторону, противоположную положительному направлению оси X.
3–Функциональную зависимость ускорения от времени найдем, используя определение ускорения как второй производной от координаты  по времени:
по времени:
 .
.
Подставим значения С,  и произведем вычисления:
и произведем вычисления: 
 .
.
4–По определению, среднее значение скорости равно:  , где S – путь, пройденный точкой за время
, где S – путь, пройденный точкой за время  .
.
Если в течение рассматриваемого промежутка времени скорость точки не изменяется по направлению, то
 ,
,
где x(t1) и x(t0) – координаты материальной точки в конечный и начальный моменты времени, соответственно.
В нашем случае в начальный момент времени  с, скорость точки равна 2 м/с, а в момент времени
с, скорость точки равна 2 м/с, а в момент времени  скорость –
скорость –  . Следовательно, в некоторый момент времени
. Следовательно, в некоторый момент времени  скорость точки обращается в нуль, т.е. в этот момент времени материальная точка изменяет направление своего движения. Тогда весь путь, пройденный точкой, можно представить в виде:
скорость точки обращается в нуль, т.е. в этот момент времени материальная точка изменяет направление своего движения. Тогда весь путь, пройденный точкой, можно представить в виде:  , где
, где  – путь, пройденный точкой до остановки, а
– путь, пройденный точкой до остановки, а 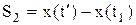 – путь, пройденный в обратном направлении.
– путь, пройденный в обратном направлении.
Найдем момент времени, в который скорость точки равна нулю:
 .
.
Отсюда  . Подставив численные значения, получим:
. Подставив численные значения, получим:  =1,155 с.
=1,155 с.
Тогда  =7,08 м,
=7,08 м,
 =4 м,
=4 м,

Cледовательно, S=(7,08-4)+(7,08-4)=6,16 м, средняя скорость <v> =3,08м/с.
Пример 2. Тело массой 10 кг движется вверх по наклонной плоскости. На тело действует сила F=100 Н, направленная вверх под углом  =
=  к поверхности наклонной плоскости. Коэффициент трения
к поверхности наклонной плоскости. Коэффициент трения  =0,1. Угол наклона плоскости
=0,1. Угол наклона плоскости  =
=  . Определить ускорение, с которым движется тело.
. Определить ускорение, с которым движется тело.

 Решение
Решение
При движении тела, кроме силы 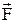 , на него действуют также: сила тяжести –
, на него действуют также: сила тяжести –  , сила реакции опоры –
, сила реакции опоры –  и сила трения –
и сила трения – 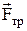 , показанные на рисунке 1.
, показанные на рисунке 1.
Ускорение тела определим, используя основной закон динамики, который в векторной форме в условиях данной задачи имеет вид:
 (1)
(1)
Направим ось X вдоль наклонной плоскости в сторону движения тела, а ось Y – перпендикулярно к ней.
Запишем уравнение (1) в проекциях на выбранные оси координат.
На ось X:  (2)
(2)
на ось Y: 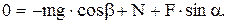 (3)
(3)
По определению, сила трения:  .
.
Силу реакции опоры найдем из уравнения (3):
 .
.
Тогда  .
.
Подставим это выражение в (2) и получим рабочую формулу:
 .
.
Проведя подстановку данных и вычисления, найдем: а=3,3м/с2.
Пример 3. К ободу однородного диска радиусом 0,2 м, вращающегося вокруг своей оси, приложена касательная сила F=98,1 Н. При вращении на диск действует момент сил трения  (рисунок 2). Найти массу диска, если известно, что диск вращается с угловым ускорением
(рисунок 2). Найти массу диска, если известно, что диск вращается с угловым ускорением  =100
=100  .
.


 Решение
Решение
Известно, что момент инерции диска относительно оси, проходящей через его центр, равен:
 .
.
Отсюда масса диска:
 . (1)
. (1)