Линейная комбинация векторов

a) вычислить 2a-3b+p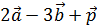

Для вычисления подобных выражений, называемых линейными комбинациями из-за того, что векторы складываются друг с другом и/или умножаются на числа, достаточно просто записать аналогичную строчку в R:

2*a-3*b+p # Вычисление вектора, равного указанной линейной комбинации

с результатом в консоли:

> 2*a-3*b+p # Вычисление вектора, равного указанной линейной комбинации векторов[1] 25 -31 43 15

Напомним, что линейные операции над векторами осуществляются покоординатно, т.е. в нашем случае должен получиться вектор

2a1-3b1+p1; 2a2-3b2+p2;…; 2a4-3b4+p4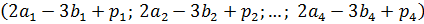

Попробуйте проверить этот результат вручную.

Скалярное произведение векторов

b) вычислить a∙b 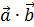и a∙p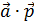

В отличие от предыдущего пункта, здесь нельзя составить обычное умножение векторов, т.к. компилятор R покоординатно перемножит векторы, что не является скалярным произведением. Вообще, важно различать покоординатное произведение векторов (не используется в векторной алгебре, но удобно в программировании):

a1b1; a2b2;…;anbn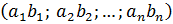

и скалярное произведение векторов (то что нам сейчас нужно):

a∙b=a1b1+a2b2+…+anbn .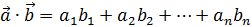

Как видите, в результате получается не вектор, а число (скаляр) – отсюда и название скалярное произведение. Желая подчеркнуть эту разницу в линейной алгебре часто используют круглые скобки для обозначения скалярного произведения: a∙b=a;b.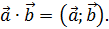

В языке R эти два приёма программируется следующим образом:

a*b # Покоординатное произведение векторов (не скалярное произведение!)

a%*%b # Скалярное произведение векторов

с результатом:

> a*b # Покоординатное произведение векторов (не скалярное произведение!)[1] -12 -27 -48 -3> a%*%b # Скалярное произведение векторов [,1][1,] -90

Обратите внимание, что результат скалярного произведения представлен в виде матрицы 1×1 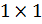, т.к. в языке R эта операция интерпретируется как частный случай произведения специальных матриц. Если мы не хотим видеть результат в виде матрицы, мы можем вывести его как обычное число:

as.numeric(a%*%b) # Скалярное произведение векторов

> as.numeric(a%*%b)[1] -90

Аналогично получим скалярное произведение a∙p :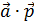

as.numeric(a%*%p) # Скалярное произведение векторов

> as.numeric(a%*%p)[1] 0

Кстати, в последнем случае результат оказался равным нулю, что говорит об ортогональности (перпендикулярности) векторов a 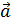и p .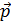

Впрочем, для нахождения скалярного произведения мы могли бы использовать простую конструкцию в виде суммы (sum) попарных произведений координат:

sum(a*p) # Фактически тоже скалярное произведение векторов

с тем же результатом.

с) вычислить a2=a∙a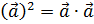

Квадрат вектора a2 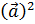понимается в векторной алгебре как скалярное произведение самого на себя a∙a 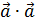, поэтому легко получить:

as.numeric(a%*%a) # Квадрат вектора

> as.numeric(a%*%a) # Квадрат вектора[1] 30

Проверьте, что результат, действительно, равен сумме квадратов координат вектора:

a2=a∙a=a1a1+a2a2+…+anan=a12+…+an2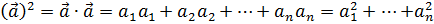

Замечание. Ошибкой было бы записать a*a или a^2, т.к. в этом случае R выдал бы покоординатное выполнение указанных операций, а не их сумму: (a12,…,an2) .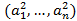

Длина вектора

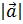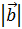d) вычислить a , b и p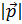

Длиной вектора называют число, равное квадратному корню из a2 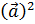и по смыслу это число является длиной отрезка, соединяющего начало и конец вектора, если его интерпретировать как направленный отрезок в евклидовой геометрии:

a=a12+…+an2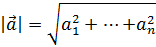

В языке R получить данное выражение можно несколькими способами. Первый из них – вызвать специальную функцию вычисления нормы элемента для вектора:

norm(a, type="2") # Длина вектора a (обычная евклидова)

с результатом:

> norm(a, type="2") # Длина вектора a (обычная евклидова)[1] 5.477226

Второй способ – образовать, согласно формуле, корень из суммы квадратов элементов:

sqrt(sum(a^2)) # Альтернатива: длина вектора a

с тем же результатом:

> sqrt(sum(a^2)) # Альтернатива: длина вектора a[1] 5.477226

Аналогично получаем для оставшихся векторов:

norm(b, type="2") # Длина вектора b (обычная евклидова)

sqrt(sum(p^2)) # Альтернатива: длина вектора p