Методы делятся на дифференциальные и интегральные. Дифференциальные используют исходное диф. ур 
. Интегральные методы используют уравнения после интегрирования. Среди интегральных методов используются: 1) подстановки 2) графический 3) определение по времени полупревращения. 1) получение опытным путём данных по зависимости концентрации реагир. вещества от времени подстановки в ур. для константы скорости р-ии различного порядка. Порядок р-ии определяется уравнением-подстановкой, в которое экспериментальных данных даёт постоянное значение константы скорости р-ии 2) экспериментальные данные представляются в виде графиков. Если в координатах 
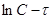получится прямая линия, то р-ия 1-го порядка. Р-ия будет иметь 2-ой порядок если прямая линия получится в координатах 
. Для р-ии 3-го порядка линия зависимости наблюдается в координатах 
. 3) р-ию проводят 2 раза с разложением начальных концентр. Каждый раз определяют время полупревращения. Если окажется, что время полупревращения не зависит от начальных концентраций, значит р-ия первого порядка, т.к. 
. Если во втором опыте начальная концентрация была увеличена в 2 раза, а время полупревращения уменьшилось в 2 раза, значит р-ия 2-го порядка, т.к. 
. Для р-ии 3-го порядка при том же самом условии время полупревращения уменьшится в 4 раза, т.к. 
. В общем случае если порядок 
, 
.
Если начальные концентрации 
, то 
, если 
, то 
. Поделив, получим 
. Логарифмируя, получим 
, 
. Это соотношение сохранится и в случае определения времени превращения любой доли концентрации 
. Прежде рассмотрим диф. метод Вант-Гоффа. В основе метода лежит Ур 
. пусть измеряемое 
, 
, 
- текущая концентрация исходного вещества в момент времени 1 и 2. 
. После логарифмирования 
, 
(1). Скорость р-ии при концентрации 
и 
определяется из зависимости 
. 
, 
Часто получают не всю кривую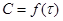 
, а производную определённой скорости при 2 концентрациях. Принимая, что 
,тогда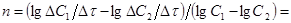 
. 
Для определения ΔС измеряем концентрации вещества в какой-то момент времени и через небольшой промежуток Δτ. Графический вариант метода Вант-Гофа W=KCn прологарифмируем 
=> является линейной функцией lgC. Определяя скорость при нескольких концентрациях, строят график lgW-lgC tgα=n. Скорость р-ии W в различный момент времени определяется как и в предыдущем случае, но тангенс угла наклона касательной к положительному направлению оси абсцисс. Определяемый таким образом порядок р-ии называется временным порядком, он учитывает влияние на порядок продолжительности р-ии. Если использовать несколько кинетических кривых, то получим истинный порядок р-ии. Время и концентрация порядка могут не совпадать. Метод изоляции. Получим выражение для константы скорости р-ии различных порядков и рассмотрим методы определения порядка р-ии применимые для тех случаев, когда кинетическое уравнение имеет вид 
. Пусть скорость хим. р-ии в зависимости от концентрации реагирующих веществ выражается Ур 
. n1, n2,.. – частные порядки р-ии или порядки р-ии соответствующие по 1-ому, 2-ому и 3-ему веществу. Сумма частных порядков определяет общий порядок р-ии. Чтобы определение частных порядков, а следовательно и общий поступают следующим образом: одно из веществ например 1-ое берут в нормальной концентрации, тогда как все остальные берут в большом избытке. Тогда концентрация этих веществ можно считать постоянными и зависимость скорости р-ии от концентрации выражается Ур 
. Одним из рассмотренных методов определён порядок р-ии по 1-ому веществу n1. Затем р-ию проводят снова, но в избытке берут все вещества, кроме 2-го и т.д.