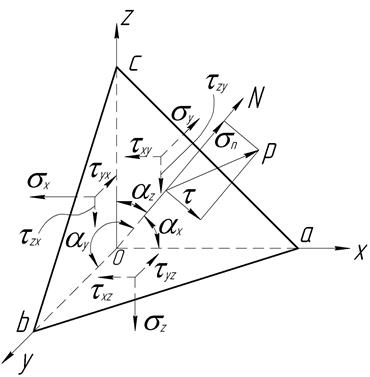
Проведем плоскость  наклоненную к осям координат. Получим фигуру тетраэдра
наклоненную к осям координат. Получим фигуру тетраэдра  , сливающуюся с точкой О при бесконечном уменьшении граней.
, сливающуюся с точкой О при бесконечном уменьшении граней.
На каждой боковой грани действуют свои напря-жения.
На наклонной площад-ке действует напряжение  . Пусть N - нормаль к наклон-ной площадке. Наклон пло-щадки к осям координат полностью определяется ее нормалью, а точнее направ-ляющими косинусами
. Пусть N - нормаль к наклон-ной площадке. Наклон пло-щадки к осям координат полностью определяется ее нормалью, а точнее направ-ляющими косинусами
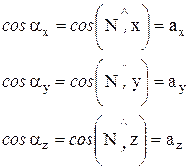
Пусть площадь 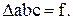
Тогда площади
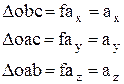
Полное напряжение  можно разложить на 3 составляющие
можно разложить на 3 составляющие 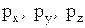 , действующие параллельно осям координат. Запишем условия равновесия тетраэдра, проецируя все действующие на его гранях силы на оси координат
, действующие параллельно осям координат. Запишем условия равновесия тетраэдра, проецируя все действующие на его гранях силы на оси координат
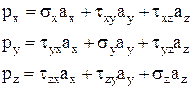 (1)
(1)
Уравнения (1) могут быть использованы для определения внешних сил 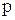 . В этом случае они играют роль уравнений связи между внешними и внутренними силами и называются условиями на контуре тела. Величину полного напряжения определим как
. В этом случае они играют роль уравнений связи между внешними и внутренними силами и называются условиями на контуре тела. Величину полного напряжения определим как
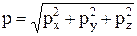 (2)
(2)
Нормальное напряжение к наклонной площадке определим, проецируя полное напряжение 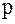 или его составляющие на нормаль N. Тогда
или его составляющие на нормаль N. Тогда
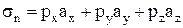 (3)
(3)
Подставляя из (1) значения 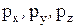 с учетом парности касательных напряжений, запишем
с учетом парности касательных напряжений, запишем
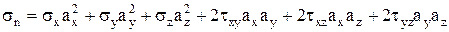 (4)
(4)
Касательное напряжение в наклонной площадке найдем по правилу паралеллограмма
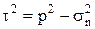 (5)
(5)
Главные напряжения
Величина действующих в наклонной площадке нормальных и касательных напряжений зависит от угла наклона площадки к осям координат. Отложим от начала координат вдоль нормали N некоторый вектор  , величина которого составляет
, величина которого составляет 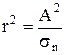 или
или 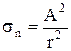 , где
, где  - некоторая произвольная постоянная. Тогда координаты конца вектора запишутся (проекции вектора по осям)
- некоторая произвольная постоянная. Тогда координаты конца вектора запишутся (проекции вектора по осям)
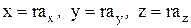
отсюда
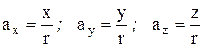
Подставив эти значения в уравнение (4), получим
 (6)
(6)
Записанное выражение является уравнением поверхности второго порядка, отнесенное к центру, поскольку здесь отсутствуют координаты 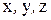 в первой степени.
в первой степени.
При изменении положения наклонной площадки будут изменяться как направление, так и координаты 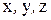 конца вектора
конца вектора  , однако конец этого вектора будет всегда совпадать с поверхностью, описанной уравнением (6).
, однако конец этого вектора будет всегда совпадать с поверхностью, описанной уравнением (6).
Отсюда следует, что данная поверхность полностью определяется напряженным состоянием точки и носит название поверхности напряжений Коши.
Из аналитической геометрии известно, что уравнение (6) второго порядка может быть преобразовано вращением координатной системы до совпадения осей координат с осями самой поверхности. Тогда пропадут члены, содержащие произведения координат, т.е. обратятся в нули. Следовательно, нулевые значения примут 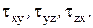 Из этого следует, что в точке тела, находящегося в напряженном состоянии, всегда можно выбрать 3 взаимноперпендикулярные площадки, в которых действуют только нормальные напряжения и отсутствуют касательные напряжения. Такие площадки называют главными, действующие в них напряжения – главными нормальными напряжениями, а направления этих напряжений – главными направлениями.
Из этого следует, что в точке тела, находящегося в напряженном состоянии, всегда можно выбрать 3 взаимноперпендикулярные площадки, в которых действуют только нормальные напряжения и отсутствуют касательные напряжения. Такие площадки называют главными, действующие в них напряжения – главными нормальными напряжениями, а направления этих напряжений – главными направлениями.
Таким образом, напряженное состояние точки вполне определено, если даны направления трех главных осей, обозначаемых индексами 1, 2, 3 вместо 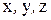 и заданы величины трех главных нормальных напряжений
и заданы величины трех главных нормальных напряжений 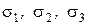 .
.
Учитывая сказанное, из выражения (1) запишем компоненты напряжений по осям
 (7)
(7)
Тогда полное напряжение из уравнения (2) будет
 ,
,
нормальное напряжение к наклонной площадке из уравнения (3) примет вид
 ,
,
а касательное из (5) запишется как
 .
.
Эллипсоид напряжений
Из выражений (7) определим направляющие косинусы
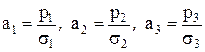 .
.
Из аналитической геометрии, известно что 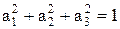 . Тогда можно записать
. Тогда можно записать
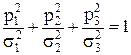 (8)
(8)
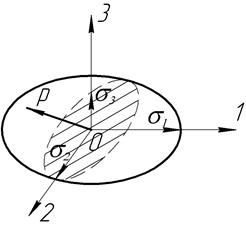
Это уравнение эллипсоида, отнесенное к центру и главным осям, который называют эллипсоидом напряжений (эллипсоидом Ламе). Полуоси его равны соответственно величинам главных напряжений, причем  .
.
Любой отрезок, проведенный от центра до пересечения с поверхностью эллипсоида, представляет собой полное напряжение 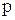 на площадке, перпендикулярной к отрезку, а проекции его на оси координат 1, 2, 3 являются составляющими
на площадке, перпендикулярной к отрезку, а проекции его на оси координат 1, 2, 3 являются составляющими 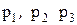 .
.
При равенстве двух главных напряжений эллипсоид напряжений обращается в эллипсоид вращения, а при равенстве трех главных напряжений – в шар.
В последнем случае любые 3 взаимноперпендикулярные оси становятся главными и во всех площадках действуют одинаковые, равные между собой, нормальные напряжения (всесторонне равномерное сжатие или растяжение).
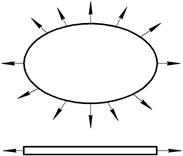 Плоское напряженное состояние с некоторым приближением может быть реализовано при растяжении тонкой пластины по контуру. Схемы объемного состояния характерны для большинства процессов ОМД.
Плоское напряженное состояние с некоторым приближением может быть реализовано при растяжении тонкой пластины по контуру. Схемы объемного состояния характерны для большинства процессов ОМД.