Определение геометрических характеристик приведенного сечения.
Отношение модулей упругости:
Площадь приведенного сечения:
Статический момент площади приведенного сечения относительной нижней грани:
Расстояние от нижней грани до центра тяжести приведенного сечения:
Момент инерции приведенного сечения:
Момент сопротивления приведенного сечения по нижней зоне:
Момент сопротивления приведенного сечения по верхней зоне:
Расстояние от ядровой точки, наиболее удаленной от растянутой зоны (верхней), до центра тяжести приведенного сечения:
то же, наименее удаленной от растянутой зоны (нижней):
здесь φn =1,6-σb/Rb,ser=1,6-0,75=0,85.
Отношение напряжения в бетоне от нормативных нагрузок и усилия обжатия к расчетному сопротивлению бетона для предельных состояний второй группы предварительно принимаю равным 0,75.
Упругопластический момент сопротивления по растянутой зоне:
здесь γ=1,75 – для таврового сечения с полкой в сжатой зоне.
Упругопластический момент сопротивления по растянутой зоне в стадии изготовления и обжатия элемента:
Здесь γ=1,5 – для таврового сечения с полкой в растянутой зоне при bf/b >2 и hf/h <0,2.
Определение потерь предварительного напряжения арматуры.
Потери от релаксации напряжений в арматуре при электротермическом способе натяжения:
Потери от температурного перепада между натянутой арматурой и упорами σ2=0, так как при пропаривании форма с упорами нагревается вместе с изделием.
Усилие обжатия:
Эксцентриситет этого усилия относительно центра тяжести приведенного сечения:
Напряжение в бетоне при обжатии:
(15)
Устанавливаю величину передаточной прочности бетона из условия
Тогда отношение
Вычисляю сжимающее напряжение в бетоне на уровне центра тяжести напрягаемой арматуры от усилия обжатия Р1 и с учетом изгибающего момента от веса плиты
тогда:
Потери от быстронатекающей ползучести при
Первые потери:
С учетом потерь σlos1 напряжение σbp=3,02 МПа. Потери от усадки бетона σ8=35 МПа. Потери от ползучести бетона при:
Вторые потери:
Полные потери:
Больше установленного минимального значения потерь.
Усилие обжатие с учетом полных потерь:
Расчет по образованию трещин, нормальных к продольной оси, производится для выяснения необходимости проверки по раскрытию трещин. При этом для элементов, к трещиностойкости которых предъявляются требования третьей категорий, принимаются значения коэффициента надежности по нагрузке γf=1; М = 
.
Расчет производится из условия M ≤ Mcrc. Вычисляем момент образования трещин по приближенному способу ядровых моментов:
Здесь ядровый момент усилия обжатия при γsp=0,84:
Поскольку М=39 кН∙м > Мcrc=10,34 кН∙м, трещины в растянутой зоне образуются. Следовательно, необходим расчёт по раскрытию трещин.
Проверим, образуются ли начальные трещины в верхней зоне плиты при ее обжатии при значении коэффициента точности натяжения γsp=1,16. Изгибающий момент от веса плиты М=16 кН∙м.
Расчетное условие:
Условие удовлетворяется, начальные трещины не образуются; здесь Rbtp=1 МПа – сопротивление бетона растяжению, соответствующие передаточной прочности бетона 
.
Расчет по раскрытию трещин,нормальных к продольной оси, при γsp=1. Предельная ширина раскрытия трещин: непродолжительная αcrc1= 
, продолжительная αcrc2= 
(см. табл. II.2). Изгибающие моменты от нормативных нагрузок: постоянной и длительной М =33,3 кН·м; суммарной М =33,3 кН·м. Приращение напряжений в растянутой арматуре от действия постоянной и длительной нагрузок по формуле (VII.102 стр. 236):
σs= 
= 
= 
= 4166 МПа,
здесь принимается z 1 
h 0-0.5 
= 27-0,5·5,75=24,1см – плечо внутренней пары сил; e sp=0, так как усилие обжатия Р приложено в центре тяжести площади нижней напрягаемой арматуры; W s= A s z 1=3,08·24,1=75см3 – момент сопротивления сечения по растянутой арматуре.
Приращение наприжений в арматуре от действия полной нагрузки
σsp= 
= 
= 
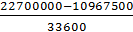= 643 МПа.
Вычисляем по формуле (VII.51 стр. 223):
Ширина раскрытия трещин от непродолжительного действия всей нагрузки
αcrc1= 14(3,5-100 
) 
= 14(3.5-100·0.0078)·1·1·1 
=
14(3.5-0,78)·1·0.022· 2.71 =14·2.72·0.0089=0.48мм;
здесь = 
= 
= 
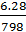= 0,0078; 
=1; η =1; φ l=1; d= 14 мм – диаметр продольной арматуры;
Ширина раскрытия трещин от непродолжительного действия постоянной и длительной нагрузок
αcrc2=20(3.5-100·0.0078)·1·1·1 
=
20(3.5-0.78)·1·0.0028·2.71=20·2.72·1·0.0028·2.71=0.41мм;
ширина раскрытия трещин от постоянной и длительной нагрузок
αcrc3=20(3.5-100·0.0078)·1·1·1.5 =
20(3.5-0.78)·1.5·0.0028·2.71=20·2.72·1.5·0.0028·2.71=0.61мм.
Непродолжительная ширина раскрытия трещин
αcr= αcrc1- αcrc2+ αcrc3=0,48-0,41+0,62=0,3мм 
.
Продолжительная ширина раскрытия трещин
αcrc= αcrc3=0.3мм ≤ .
Расчет прогиба плиты. Прогиб определяется от нормативногозначения постоянной и длительной нагрузок, предельный прогиб f = 
согласно табл. II.4. Вычисляем параметры, необходмые для определения прогиба плиты с учетом трещин в растянутой зоне. Заменяющий момент равен изгибающему моменту от постоянной и длительной нагрузок М =33,3кН·м; суммарная продольная сила равна усилию предварительного обжатия с учетом всех потерь и при γsp=1, N tot= P 2=85 кН;
экцентриситет e s,tot= M / N tot=33300000/85000=391.7см;
коэффициент γ l =0.8 при длительном действии нагрузки; (VII.5 стр. 230)
γm= 
= 
= 
= 0.1 < 1;
коэффициент характеризующий неравномерности деформаций расянутой арматуры на участке между трещинами, по формуле (VII.74 стр.230):
ψs=1.25- φ l φm- 
= 1.25-0.8·0.1- 
=
1.25- 0.08- 
= 1.25-0.08-0.18=0.9 ≤ 1.
Вычисляем кривизну оси при изгибе по формуле (VII.125 стр.241):
= 
- 
=
- 
· 
=
- · 
=
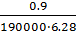0.062·103·0.0085·10-4·0.0027·10-2=1.4·10-3см-1,
здесь ψ=0,9; λb=0.15 – при длительном действии нагрузок
A b=(
+ξ) bh 0= 
=296·7=2072см2 в соответствии с формулой (VII.87)
при 
=0 и допущением, что ξ= / h 0.
Вычисляем прогиб по формуле (VII.131)
f = 
· 
= ·118002·1.4·10-3=0.1·139240000·0.014·10-3=
194936·10-3=1.9< .
Учет прогиба от ползучести бетона в следствии обжатия по формуле(VII.114) несколько уменьшает прогиб.
Расчет по образованию и раскрытию трещин, наклонных к продольной оси ребристой плиты, выполняется по данным §VII.1, п.5 и § VII.3, п.2.