Корреляционный анализ так же проведен с использованием программы Statistica. В результате некоторых преобразований была получена таблица 4. Далее при дальнейших преобразованиях в программе были получены некоторые диаграммы зависимостей рассеяния.
Таблица 4
Результаты корреляционного анализа по всем элементам
| SiO2 | TiO2 | Al2O3 | Fe2O3 | MnO | MgO | CaO | Na2O | K2O | P2O5 | ППП | |
| SiO2 | 1,00 | ||||||||||
| TiO2 | -0,74 | 1,00 | |||||||||
| Al2O3 | -0,87 | 0,63 | 1,00 | ||||||||
| Fe2O3 | -0,75 | 0,62 | 0,56 | 1,00 | |||||||
| MnO | -0,64 | 0,38 | 0,42 | 0,69 | 1,00 | ||||||
| MgO | -0,54 | 0,31 | 0,49 | 0,65 | 0,31 | 1,00 | |||||
| CaO | -0,57 | 0,23 | 0,28 | 0,46 | 0,70 | 0,47 | 1,00 | ||||
| Na2O | -0,14 | 0,17 | 0,11 | -0,02 | 0,10 | -0,24 | -0,23 | 1,00 | |||
| K2O | 0,34 | -0,33 | -0,36 | -0,69 | -0,54 | -0,48 | -0,21 | -0,23 | 1,00 | ||
| P2O5 | -0,68 | 0,84 | 0,48 | 0,62 | 0,42 | 0,34 | 0,22 | 0,13 | -0,28 | 1,00 | |
| ППП | -0,66 | 0,36 | 0,55 | 0,78 | 0,76 | 0,48 | 0,59 | -0,16 | -0,62 | 0,36 | 1,00 |

| 
|

| 
|

| 
|
Рисунок 6 – Диаграммы рассеяния некоторых элементов
Регрессионный анализ
В линейный регрессионный анализ входит широкий круг задач, связанных с построением (восстановлением) зависимостей между группами числовых переменных  .
.
Предполагается, что X - независимые переменные (предикторы, объясняющие переменные) влияют на значения Y - зависимых переменных (откликов, объясняемых переменных). По имеющимся эмпирическим данным  требуется построить функцию
требуется построить функцию 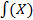 , которая приближенно описывала бы изменение Y при изменении X:
, которая приближенно описывала бы изменение Y при изменении X: 
Предполагается, что множество допустимых функций, из которого подбирается 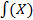 является параметрическим:
является параметрическим: 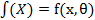
где -  неизвестный параметр (вообще говоря, многомерный). При построении
неизвестный параметр (вообще говоря, многомерный). При построении 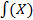 будем считать, что
будем считать, что 
где первое слагаемое – закономерное изменение Y от X, а второе - ε - случайная составляющая с нулевым средним;  является условным математическим ожиданием Y при условии известного X и называется регрессией Y по X.
является условным математическим ожиданием Y при условии известного X и называется регрессией Y по X.
Пусть n раз измерены значения факторов  и соответствующие значения переменной y; предполагается, что
и соответствующие значения переменной y; предполагается, что 
(второй индекс у x относится к номеру фактора, а первый – к номеру наблюдения); предполагается также, что 

т.е.  - некоррелированные случайные величины. Соотношения (2) удобно записывать в матричной форме:
- некоррелированные случайные величины. Соотношения (2) удобно записывать в матричной форме: 
где  вектор-столбец значений зависимой переменной, t - символ транспонирования,
вектор-столбец значений зависимой переменной, t - символ транспонирования,  вектор-столбец (размерности k) неизвестных коэффициентов регрессии,
вектор-столбец (размерности k) неизвестных коэффициентов регрессии,  - вектор случайных отклонений,
- вектор случайных отклонений,


-матрица  ; в i -й строке
; в i -й строке  находятся значения независимых переменных в i -м наблюдении первая переменная – константа, равная 1.
находятся значения независимых переменных в i -м наблюдении первая переменная – константа, равная 1.
Построим оценку β для вектора β так, чтобы вектор оценок  зависимой переменной минимально (в смысле квадрата нормы разности) отличался от вектора
зависимой переменной минимально (в смысле квадрата нормы разности) отличался от вектора  заданных значений:
заданных значений: 
Решением является (если ранг матрицы X равен k+1 оценка

Нетрудно проверить, что она несмещенная.
Таблица №5. Предсказанные значения и остатки, зависимая переменная TiO2
| Наблюд. | Предск. | Остатки | Станд. | Станд. | Стд.Ош. | Махалан. | Удален. | Кука | |
| Значение | Значение | предск. | Остатки | предск. | расст. | остатки | расст. | ||
| 0,130 | 0,193 | -0,063 | -0,612 | -0,580 | 0,023 | 0,375 | -0,066 | 0,009 | |
| 0,660 | 0,487 | 0,173 | 1,152 | 1,593 | 0,031 | 1,328 | 0,188 | 0,118 | |
| 0,600 | 0,516 | 0,084 | 1,329 | 0,770 | 0,033 | 1,765 | 0,092 | 0,034 | |
| 0,610 | 0,546 | 0,064 | 1,505 | 0,592 | 0,036 | 2,265 | 0,072 | 0,025 | |
| 0,350 | 0,311 | 0,039 | 0,094 | 0,363 | 0,020 | 0,009 | 0,041 | 0,002 | |
| 0,110 | 0,193 | -0,083 | -0,612 | -0,765 | 0,023 | 0,375 | -0,087 | 0,015 | |
| 0,160 | 0,252 | -0,092 | -0,259 | -0,845 | 0,021 | 0,067 | -0,095 | 0,014 | |
| 0,230 | 0,252 | -0,022 | -0,259 | -0,201 | 0,021 | 0,067 | -0,023 | 0,001 | |
| 0,150 | 0,252 | -0,102 | -0,259 | -0,937 | 0,021 | 0,067 | -0,106 | 0,017 | |
| 0,390 | 0,311 | 0,079 | 0,094 | 0,731 | 0,020 | 0,009 | 0,082 | 0,010 | |
| 0,080 | 0,252 | -0,172 | -0,259 | -1,582 | 0,021 | 0,067 | -0,178 | 0,048 | |
| 0,340 | 0,340 | 0,000 | 0,270 | 0,000 | 0,021 | 0,073 | 0,000 | 0,000 | |
| 0,273 | 0,228 | 0,045 | -0,401 | 0,411 | 0,021 | 0,160 | 0,046 | 0,004 | |
| 0,248 | 0,134 | 0,114 | -0,965 | 1,047 | 0,028 | 0,932 | 0,122 | 0,041 | |
| 0,010 | 0,134 | -0,124 | -0,965 | -1,144 | 0,028 | 0,932 | -0,133 | 0,049 | |
| 0,380 | 0,660 | -0,280 | 2,193 | -2,580 | 0,048 | 4,810 | -0,350 | 1,034 | |
| 0,093 | 0,134 | -0,041 | -0,965 | -0,380 | 0,028 | 0,932 | -0,044 | 0,005 | |
| 0,281 | 0,134 | 0,147 | -0,965 | 1,350 | 0,028 | 0,932 | 0,157 | 0,068 | |
| 0,039 | 0,134 | -0,095 | -0,965 | -0,877 | 0,028 | 0,932 | -0,102 | 0,029 | |
| 0,131 | 0,134 | -0,003 | -0,965 | -0,030 | 0,028 | 0,932 | -0,004 | 0,000 | |
| 0,326 | 0,243 | 0,083 | -0,312 | 0,764 | 0,021 | 0,098 | 0,086 | 0,012 | |
| 0,363 | 0,269 | 0,094 | -0,154 | 0,861 | 0,020 | 0,024 | 0,097 | 0,014 | |
| 0,366 | 0,328 | 0,038 | 0,199 | 0,348 | 0,020 | 0,040 | 0,039 | 0,002 | |
| 0,213 | 0,343 | -0,130 | 0,288 | -1,196 | 0,021 | 0,083 | -0,135 | 0,028 | |
| 0,401 | 0,396 | 0,005 | 0,605 | 0,048 | 0,023 | 0,366 | 0,005 | 0,000 | |
| 0,855 | 0,807 | 0,048 | 3,075 | 0,440 | 0,065 | 9,459 | 0,075 | 0,085 | |
| 0,454 | 0,275 | 0,179 | -0,118 | 1,644 | 0,020 | 0,014 | 0,185 | 0,049 | |
| 0,228 | 0,134 | 0,094 | -0,965 | 0,862 | 0,028 | 0,932 | 0,100 | 0,028 | |
| 0,077 | 0,134 | -0,057 | -0,965 | -0,527 | 0,028 | 0,932 | -0,061 | 0,010 | |
| 0,303 | 0,322 | -0,019 | 0,164 | -0,178 | 0,020 | 0,027 | -0,020 | 0,001 | |
| Минимум | 0,010 | 0,134 | -0,280 | -0,965 | -2,580 | 0,020 | 0,009 | -0,350 | 0,000 |
| Максим. | 0,855 | 0,807 | 0,179 | 3,075 | 1,644 | 0,065 | 9,459 | 0,188 | 1,034 |
| Среднее | 0,295 | 0,295 | 0,000 | 0,000 | 0,000 | 0,026 | 0,967 | -0,001 | 0,058 |
| Медиана | 0,277 | 0,252 | 0,003 | -0,259 | 0,024 | 0,023 | 0,371 | 0,003 | 0,014 |
Таблица №6.
Предсказанные значения и остатки, с зависимой переменной MgO
| Наблюд. | Предск. | Остатки | Станд. | Станд. | Стд.Ош. | Махалан. | Удален. | Кука | |
| Значение | Значение | предск. | Остатки | предск. | расст. | остатки | расст. | ||
| 0,470 | 0,452 | 0,018 | -0,555 | 0,029 | 0,131 | 0,308 | 0,019 | 0,000 | |
| 1,700 | 0,979 | 0,721 | 2,125 | 1,158 | 0,271 | 4,514 | 0,889 | 0,193 | |
| 1,440 | 0,602 | 0,838 | 0,211 | 1,344 | 0,116 | 0,044 | 0,868 | 0,034 | |
| 1,740 | 0,753 | 0,987 | 0,976 | 1,584 | 0,160 | 0,953 | 1,057 | 0,095 | |
| 0,800 | 1,054 | -0,254 | 2,508 | -0,407 | 0,312 | 6,288 | -0,339 | 0,037 | |
| 0,060 | 0,452 | -0,392 | -0,555 | -0,629 | 0,131 | 0,308 | -0,410 | 0,009 | |
| 0,420 | 0,677 | -0,257 | 0,593 | -0,413 | 0,133 | 0,352 | -0,270 | 0,004 | |
| 0,850 | 0,677 | 0,173 | 0,593 | 0,277 | 0,133 | 0,352 | 0,181 | 0,002 | |
| 0,610 | 0,753 | -0,143 | 0,976 | -0,229 | 0,160 | 0,953 | -0,153 | 0,002 | |
| 0,400 | 0,677 | -0,277 | 0,593 | -0,445 | 0,133 | 0,352 | -0,291 | 0,005 | |
| 0,050 | 0,903 | -0,853 | 1,742 | -1,369 | 0,231 | 3,034 | -0,990 | 0,174 | |
| 0,840 | 0,677 | 0,163 | 0,593 | 0,261 | 0,133 | 0,352 | 0,170 | 0,002 | |
| 1,596 | 0,384 | 1,212 | -0,900 | 1,945 | 0,154 | 0,809 | 1,291 | 0,131 | |
| 1,789 | 0,595 | 1,194 | 0,172 | 1,917 | 0,116 | 0,030 | 1,237 | 0,068 | |
| 1,229 | 0,309 | 0,920 | -1,282 | 1,477 | 0,187 | 1,645 | 1,011 | 0,119 | |
| 1,758 | 0,497 | 1,261 | -0,325 | 2,024 | 0,120 | 0,106 | 1,310 | 0,082 | |
| 0,076 | 0,391 | -0,315 | -0,861 | -0,506 | 0,151 | 0,742 | -0,335 | 0,009 | |
| 0,066 | 0,384 | -0,318 | -0,900 | -0,510 | 0,154 | 0,809 | -0,339 | 0,009 | |
| 0,068 | 0,309 | -0,241 | -1,282 | -0,386 | 0,187 | 1,645 | -0,264 | 0,008 | |
| 0,060 | 0,376 | -0,316 | -0,938 | -0,508 | 0,157 | 0,880 | -0,338 | 0,009 | |
| 0,069 | 0,534 | -0,465 | -0,134 | -0,747 | 0,115 | 0,018 | -0,482 | 0,010 | |
| 0,086 | 0,452 | -0,366 | -0,555 | -0,587 | 0,131 | 0,308 | -0,382 | 0,008 | |
| 0,094 | 0,437 | -0,343 | -0,632 | -0,550 | 0,135 | 0,399 | -0,360 | 0,008 | |
| 0,076 | 0,730 | -0,654 | 0,861 | -1,050 | 0,151 | 0,742 | -0,695 | 0,037 | |
| 0,085 | 0,444 | -0,359 | -0,593 | -0,576 | 0,133 | 0,352 | -0,376 | 0,008 | |
| 0,114 | 0,640 | -0,526 | 0,402 | -0,844 | 0,123 | 0,162 | -0,547 | 0,015 | |
| 0,063 | 0,482 | -0,419 | -0,402 | -0,672 | 0,123 | 0,162 | -0,436 | 0,010 | |
| 0,060 | 0,354 | -0,294 | -1,053 | -0,471 | 0,167 | 1,108 | -0,316 | 0,009 | |
| 0,077 | 0,346 | -0,269 | -1,091 | -0,432 | 0,170 | 1,190 | -0,291 | 0,008 | |
| 0,078 | 0,504 | -0,426 | -0,287 | -0,684 | 0,119 | 0,082 | -0,442 | 0,009 | |
| Минимум | 0,050 | 0,309 | -0,853 | -1,282 | -1,369 | 0,115 | 0,018 | -0,990 | 0,000 |
| Максим. | 1,789 | 1,054 | 1,261 | 2,508 | 2,024 | 0,312 | 6,288 | 1,310 | 0,193 |
| Среднее | 0,561 | 0,561 | 0,000 | 0,000 | 0,000 | 0,155 | 0,967 | -0,001 | 0,037 |
| Медиана | 0,104 | 0,501 | -0,273 | -0,306 | -0,439 | 0,134 | 0,376 | -0,304 | 0,009 |

Рисунок 7 - Нормальный вероятный график по TiO2
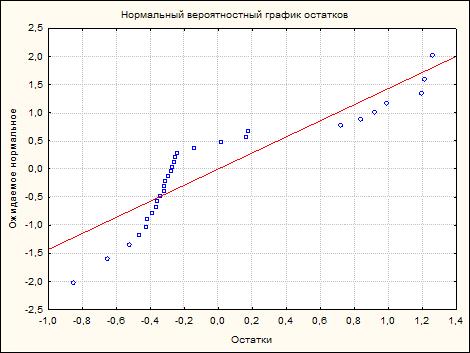
Рисунок 8 - Нормальный вероятный график по MgO
Множественная линейная регрессия предполагает линейную связь между переменными в уравнении, и нормальным распределением остатков. Если эти предположения нарушаются, окончательные заключения могут оказаться неточными. Нормальный вероятностный график остатков наглядно показывает наличие или отсутствие больших отклонений от высказанных предположений.
Кластерный анализ
Кластерный анализ — это общий термин для целого ряда методов, используемых для группировки объектов, событий или индивидов в классы (кластеры) на основе сходства их характерных признаков. Несмотря на отсутствие единого определения кластера, во всех его определениях особо подчеркиваются такие условия, как сходство, однородность и близость. Если воспользоваться специальной терминологией, то кластеры можно определить, как однородные подгруппы, формируемые методом, который минимизирует дисперсию внутри групп (кластеров) и максимизирует дисперсию между группами.
Методики кластеризации используются для установления сходных подгрупп объектов или индивидов и для построения таксономии. Таким образом, они помогают исследователю в описании структуры совокупности объектов и отношений между ними, а также в формулировании законов и утверждений относительно классов объектов.
Если обобщить различные классификации методов кластеризации, то можно выделить ряд групп (некоторые методы можно отнести сразу к нескольким группам и потому предлагается рассматривать данную типизацию как некоторое приближение к реальной классификации методов кластеризации): [5]
1. Вероятностный подход. Предполагается, что каждый рассматриваемый объект относится к одному из k классов.
· K-средних (K-means)
· K-medians
· EM-алгоритм
· Алгоритмы семейства FOREL
· Дискриминантный анализ
2. Подходы на основе систем искусственного интеллекта. Весьма условная группа, так как методов AI очень много и методически они весьма различны.
· Метод нечеткой кластеризации C-средних (C-means)
· Нейронная сеть Кохонена
· Генетический алгоритм
3. Логический подход. Построение дендрограммы осуществляется с помощью дерева решений.
4. Теоретико-графовый подход.
· Графовые алгоритмы кластеризации
5. Иерархический подход. Предполагается наличие вложенных групп (кластеров различного порядка). Алгоритмы в свою очередь подразделяются на агломеративные (объединительные) и дивизивные (разделяющие). По количеству признаков иногда выделяют монотетические и политетические методы классификации.
· Иерархическая дивизивная кластеризация или таксономия. Задачи кластеризации рассматриваются в количественной таксономии.
6. Другие методы. Не вошедшие в предыдущие группы.
· Статистические алгоритмы кластеризации
· Ансамбль кластеризаторов
· Алгоритмы семейства KRAB
· Алгоритм, основанный на методе просеивания
· DBSCAN и др.
Подходы 4 и 5 иногда объединяют под названием структурного или геометрического подхода, обладающего большей формализованностью понятия близости [2]. Несмотря на значительные различия между перечисленными методами все они опираются на исходную «гипотезу компактности»: в пространстве объектов все близкие объекты должны относиться к одному кластеру, а все различные объекты соответственно должны находиться в различных кластерах.
Все методы кластерного анализа состоят из четырех основных шагов: а) выбор мер и произведение измерений характерных признаков объектов или индивидов, подлежащих классификации; б) задание меры сходства; в) формулирование правил и определение порядка формирования кластеров; г) применение этих правил к данным для формирования кластеров. Так как каждый шаг предполагает выбор из множества возможных процедур, был разработан широкий спектр методик кластеризации.
На первом шаге принимается решение о том, какие характерные признаки или свойства будут использоваться в качестве основы классификации. Конечно, это решение будет зависеть от проблемы исследования и природы классифицируемых объектов. Хотя обычно все признаки имеют одинаковые веса, не исключается возможность выбора процедуры приписывания различных весов.
Принимаемое на втором шаге решение связано с выбором подходящей меры сходства. Это может быть число общих признаков, корреляция между признаками, метрика (пространства классификации) или к.-л. др. мера.
На третьем шаге выбирается сам метод классификации. Агломеративные методы начинают с анализа отдельных объектов или индивидов и объединяют их в группы; методы расслоения начинают с анализа полной группы и делят ее на подгруппы. Классификация по одному признаку приводят к классам, все элементы которых имеют по крайней мере один общий отличительный признак; классификация, основывается на сравнении нескольких признаков, приводят к группам, которые обладают рядом общих свойств, но не обязательно обладают одним общим отличительным признаком.
Принимаемое на четвертом шаге решение касается момента остановки процедуры классификации или, проще говоря, определения количества сформированных групп. Это может определяться как внутренними критериями (например, естественным разбиением полной группы на подгруппы), так и внешними критериями (т. е. тем, какая схема классификации приводит к наиболее полезным закономерностям). Наконец, необходимо решить, будет ли использоваться иерархическая или неиерархическая схема классификации. При выборе иерархической схемы сформированные группы будут находиться на различных уровнях обобщенности (как в биологических таксономиях); в случае выбора неиерархической схемы получаются группы одного уровня обобщенности (как при использовании Q-техники факторного анализа). Результаты этих решений будут определять подходящий метод кластерного анализа и характер сформированных кластеров.