Введение
Фильтр это частотно-избирательное устройство, которое пропускает сигналы определенных частот и задерживает или ослабляет сигналы других частот.
Фильтры обеспечивают выделение полезной информации из смеси информационного сигнала с помехой с требуемыми показателями. Основная задача выбора типа фильтра и его расчета заключается в получении таких параметров, которые обеспечивают максимальную вероятность обнаружения информационного сигнала на фоне помех.
Активный фильтр - один из видов аналоговых электронных фильтров, в котором присутствует одна или несколько активных компонент, к примеру, транзистор или операционный усилитель. Эти обладающие частотной избирательностью схемы используются для усиления или ослабления определенных частот в звуковой аппаратуре, в генераторах электромузыкальных инструментов, в сейсмических приборах, в линиях связи и т.п.
Использование активных фильтров привлекательно по целому ряду причин и может быть предпочтительней пассивных RLС - эквнвалентов. Например, активные RС-фильтры обычно имеют меньшую массу и занимают меньше места, чем пассивные. Это имеет большое значение при использовании фильтров в аэрокосмических приборах. Другое преимущество - активные фильтры могут быть изготовлены в микромодульном исполнении при использовании технологии интегральных микросхем. Кроме того, они относительно недороги и могут производиться в массовом масштабе. С другой стороны, так как катушка индуктивности не может быть выполнена в интегральном исполнении, то пассивные схемы можно создать только с помощью дискретных компонентов. Этот вариант значительно дороже. По этим и ряду других причин во многих традиционных областях применения фильтров, особенно в радиосвязи, приходится проводить модернизацию, направленную на исключительное использование активных фильтров. В результате этого ежегодное производство активных фильтров оценивается миллионами, и многие компании предлагают их как стандартные блоки.
|
|
С помощью активных RC - фильтров нельзя получить идеальные формы частотных характеристик в виде прямоугольников со строго постоянным коэффициентом передачи в полосе пропускания, бесконечным ослаблением в полосе подавления и бесконечной крутизной спада при переходе от полосы пропускания к полосе подавления. Также к недостаткам активных фильтров можно отнести необходимость использования источника питания и невозможность работы на таких высоких частотах, на которых активные элементы уже не способны усиливать сигнал. Проектирование активного фильтра всегда представляет собой поиск компромисса между идеальной формой характеристики и сложностью её реализации. Это называется «проблемой аппроксимации».
Во многих случаях требования к качеству фильтрации позволяют обойтись простейшими фильтрами первого или второго порядка. Проектирование фильтра в этом случае сводится к выбору схемы с наиболее подходящей конфигурацией и последующему расчету значений номиналов элементов для конкретных частот.
Математическое описание фильтров
Основной характеристикой фильтра считается его амплитудно-частотная характеристика (АЧХ), отображающая зависимость коэффициента передачи фильтра К(ω) от угловой частоты сигнала. По виду АЧХ фильтры разделяются на: фильтры нижних частот (ФНЧ) (пропускают низкие частоты и задерживают высокие частоты), фильтры верхних частот (ФВЧ) (пропускают высокие частоты и задерживают низкие частоты), полосовые фильтры (ПФ) (пропускают полосу частот и задерживают те частоты, которые расположены выше и ниже этой полосы) и режекторные (заграждающие) фильтры (задерживают полосу частот и пропускают частоты, расположенные выше и ниже этой полосы). На рисунке 1 представлены АЧХ фильтров низких и высоких частот.
|
|
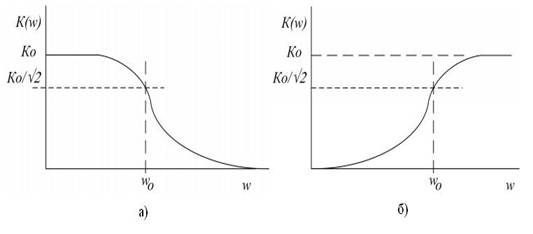
Рис. 1. Амплитудно-частотные характеристики: а) ФНЧ; б) ФВЧ
Для описания ФНЧ и ФВЧ вводится понятие частоты среза ω0 - частоты сигнала, на которой наблюдается уменьшение мощности в 2 раза. Коэффициент передачи фильтра при этом уменьшается в √2 раз по сравнению с коэффициентом передачи К0 на нулевой (для ФНЧ) или на бесконечной (для ФВЧ) частоте.
Рассматриваемые активные RC-фильтры относят к классу линейных электрических цепей с сосредоточенными и постоянными во времени параметрами, передаточная функция которых имеет вид:
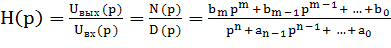, (1)фильтр
где Uвх(p), Uвх(p) - изображения по Лапласу входного и выходного напряжений;
p=σ+jω - комплексная переменная;
ai, bi - вещественные коэффициенты, зависящие от параметров цепи; К - масштабный множитель (коэффициент усиления).
Степень полинома знаменателя n определяет порядок фильтра. Реальные амплитудно-частотные характеристики лучше (более близки к идеальным) для фильтров более высокого порядка. Однако повышение порядка связано с усложнением схем и более высокой стоимостью. Таким образом, один из аспектов разработки фильтров связан с получением реализуемой характеристики, аппроксимирующей с некоторой заданной степенью точности идеальную характеристику при наименьших затратах.
|
|
Если в формуле (1) все коэффициенты а равны нулю, за исключением а0, то передаточная функция представляет собой отношение постоянного числа к полиному. В этом случае фильтр является всеполюсным или полиномиальным, поскольку его передаточная функция обладает тем свойством, что все ее полюсы конечны, а конечных нулей не содержит. Нуль определяется значением переменной p, для которой передаточная функция равна нулю, а полюс - это значение переменной p, для которой передаточная функция имеет бесконечное значение.
Для ФНЧ первого порядка передаточная функция представляется в виде:
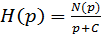, (2)
где С - постоянное число, а N(p) - полином первой или нулевой степени.
Для ФНЧ второго порядка передаточная функция представляется в виде:
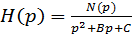, (3)
где В и С - постоянные числа, а N(p) - полином второй или меньшей степени.
Для четного порядка n>2 обычная каскадная схема содержит n/2 звеньев второго порядка, каждое с передаточной функцией типа (3). Если же порядок n>2 является нечетным, то схема содержит (n-l)/2 звеньев второго порядка с передаточными функциями типа (3) и одно звено первого порядка с передаточной функцией типа (2).
Передаточную функцию фильтра верхних частот с частотой среза ωс можно получить из передаточной функции нормированного фильтра нижних частот (имеющего ωс, равную 1 рад/с) с помощью замены переменной p на ωс/p. Следовательно, функция фильтров верхних частот Баттерворта и Чебышева будет содержать следующие сомножители второго порядка:
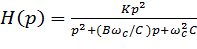, (4)
где ωс - частота среза, а В и С представляют собой приведенные в приложении А нормированные коэффициенты звена фильтра нижних частот второго порядка. При нечетном порядке присутствует также звено первого порядка, обладающее передаточной функцией вида:
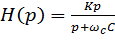. (5)
Коэффициент усиления фильтра верхних частот представляет собой значение его передаточной функции при бесконечном значении переменной s. Следовательно, для звеньев второго и первого порядков ФВЧ, описываемых соответственно уравнениями (4) и (5), коэффициент усиления звена равен К.
B процессе проектирования параметры передаточной функции фильтра могут выбираться и оптимизироваться по различным критериям. Критериями чаще всего выступают равномерность АЧХ и колебательность переходной характеристики фильтра h(t). Наиболее известны методики расчета, основанные на использовании алгебраических полиномов с известными свойствами, предложенных в своё время математиками Бесселем, Баттервортом и Чебышевым. Фильтры с использованием этих полиномов получили соответствующие имена.
На рисунке 2 для сравнения показаны АЧХ фильтров нижних частот различных типов.
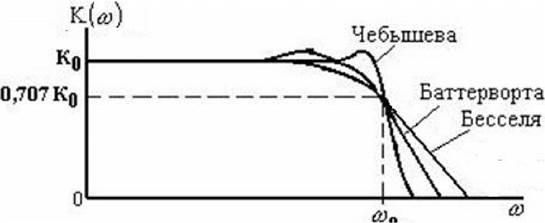
Рис.2. Сравнительные АЧХ фильтров низкой частоты
Фильтр Баттерворта
Передаточная функция фильтра нижних частот Баттерворта n -го порядка характеризуется выражением:
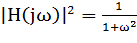. (6)
Амплитудно-частотная характеристика фильтра Баттерворта обладает следующими свойствами:
1) при любом порядке n значение АЧХ: │H(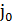
)│= 1;
2) на частоте среза ω=ωс;│H(j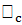 
) │=0.707.
АЧХ ФНЧ монотонно убывает с ростом частоты. По этой причине фильтры Баттерворта называют фильтрами с максимально плоскими характеристиками. На рисунке 3 показаны графики амплитудно-частотных характеристик ФНЧ Баттерворта 1-5 порядков. Очевидно, что чем больше порядок фильтра, тем точнее аппроксимируется АЧХ идеального фильтра нижних частот.
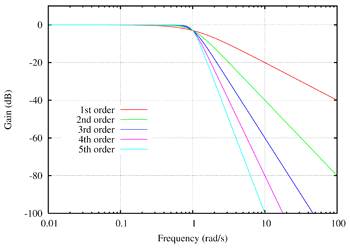
Рис. 3. АЧХ для фильтра Баттерворта нижних частот порядка от 1 до 5.
На рисунке 4 представлена схемная реализация ФВЧ Баттерворта.
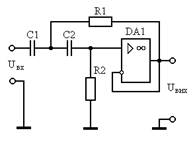
Рис. 4. ФВЧ-II Баттерворта.
Достоинством фильтра Баттерворта является максимально гладкая АЧХ на частотах полосы пропускания и ее снижение практически до нуля на частотах полосы подавления. Фильтр Баттерворта - единственный из фильтров, сохраняющий форму АЧХ для более высоких порядков (за исключением более крутого спада характеристики на полосе подавления) тогда как многие другие разновидности фильтров (фильтр Бесселя, фильтр Чебышева, эллиптический фильтр) имеют различные формы АЧХ при различных порядках.
Однако в сравнении с фильтрами Чебышева I и II типов или эллиптическим фильтром, фильтр Баттерворта имеет более пологий спад характеристики и поэтому должен иметь больший порядок (что более трудно в реализации) для того, чтобы обеспечить нужные характеристики на частотах полосы подавления.
Фильтр Чебышева
Квадрат модуля передаточной функции фильтра Чебышева определяется выражением:
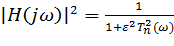, (7)
где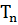 
(ꞷ)- полином Чебышева. Модуль передаточной функции фильтра Чебышева равен единице на тех частотах, где 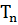(ꞷ) обращается в нуль.
Фильтры Чебышева обычно используются там, где требуется с помощью фильтра небольшого порядка обеспечить требуемые характеристики АЧХ, в частности, хорошее подавление частот из полосы подавления, и при этом гладкость АЧХ на частотах полос пропускания и подавления не столь важна.
Различают фильтры Чебышева I и II родов.
Фильтр Чебышева I рода. Это более часто встречающаяся модификация фильтров Чебышева. В полосе пропускания такого фильтра видны пульсации, амплитуда которых определяется показателем пульсации ε. В случае аналогового электронного фильтра Чебышева его порядок равен числу реактивных компонентов, использованных при его реализации. Более крутой спад характеристики может быть получен если допустить пульсации не только в полосе пропускания, но и в полосе подавления, добавив в передаточную функцию фильтра нулей на мнимой оси jω в комплексной плоскости. Это, однако, приведёт к меньшему эффективному подавлению в полосе подавления. Полученный фильтр является эллиптическим фильтром, также известным как фильтр Кауэра.
АЧХ для фильтра Чебышева нижних частот I рода четвёртого порядка представлена на рисунке 5.
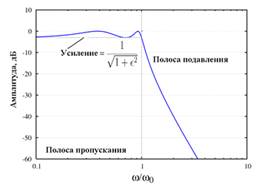
Рис. 5. АЧХ для фильтра Чебышева нижних частот I рода четвёртого порядка
Фильтр Чебышева II рода (инверсный фильтр Чебышева) используется реже, чем фильтр Чебышева I рода ввиду менее крутого спада амплитудной характеристики, что приводит к увеличению числа компонентов. У него отсутствуют пульсации в полосе пропускания, однако присутствуют в полосе подавления.
АЧХ для фильтра Чебышева нижних частот II рода четвёртого порядка представлена на рисунке 6.
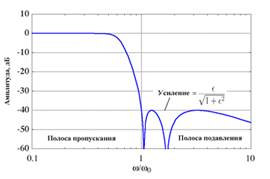
Рис. 6. АЧХ для фильтра Чебышева нижних частот II рода
На рисунке 7 представлены схемные реализации ФВЧ Чебышева I и II порядка.
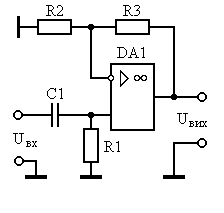
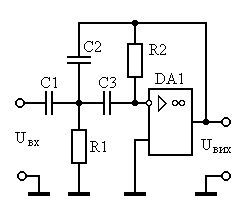
а) б)
Рис. 7. ФВЧ Чебышева: а) I порядка; б) II порядка
Свойства частотных характеристик фильтров Чебышева:
1) В полосе пропускания АЧХ имеет равноволновой характер. На интервале (-1≤ω≤1) имеется n точек, в которых функция│H(jꞷ)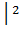 
достигает максимального значения, равного 1, или минимального значения, равного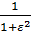 
Если n нечетно, │H(j0)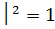 
; если n четно │H(j0) │= 
;
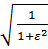2) значение АЧХ фильтра Чебышева на частоте среза равно │H(j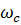 
) │= ;
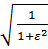3) При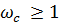 
функция монотонно убывает и стремится к нулю.
4) Параметр ε определяет неравномерность АЧХ фильтра Чебышева в полосе пропускания:
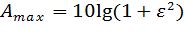(8)
Сравнение АЧХ фильтров Баттерворта и Чебышева показывает, что фильтр Чебышева обеспечивает большее ослабление в полосе пропускания, чем фильтр Баттерворта такого же порядка. Недостаток фильтров Чебышева заключается в том, что их фазочастотные характеристики в полосе пропускания значительно отличаются от линейных.
Для фильтров Баттерворта и Чебышева имеются подробные таблицы, в которых приведены координаты полюсов и коэффициенты передаточных функций различных порядков.
Список использованной литературы
1. Гутников, В. Фильтрация измерительных сигналов/ Гутников В.С. - Л.: Энергоатомиздат, 1990.- 192с., ил.
2. Джонсон, Д. Справочник по активным фильтрам: Пер. с англ./ Д.Джонсон, Дж. Джонсон, Г. Мур - М.: Энергоатомиздат, 1983. - 128с., ил.
3. Довгун, В. П. Электротехника и электроника: учеб. пособие: в 2-х ч. Ч. 2 / В. П. Довгун. - Красноярск: ИПЦ КГТУ, 2006. - 252 с.
4. Капустян, В. Активные RC-фильтры высокого порядка/ Капустян В.И. - М.: Радио и связь, 1985. - 248с., ил.
5. Мошиц Г. П. Проектирование активных фильтров: пер. с англ. / Г. Мошиц, П. Хорн. - М.: Мир, 1984. - 320 с., ил.
6. Хоровиц, П. Искусство схемотехники / П. Хоровиц, У. Хилл: пер. с англ. - 6-е изд. - М.: Мир, 2003. - 704 с., ил.