Энергия взаимодействия двух точечных зарядов
Так как между точечными зарядами есть силы притяжения или отталкивания, можно говорить о потенциальной энергии взаимодействия.
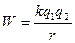. Правильный знак у энергии получается автоматически. При взаимодействии разноименных зарядов потенциальная энергия отрицательная.
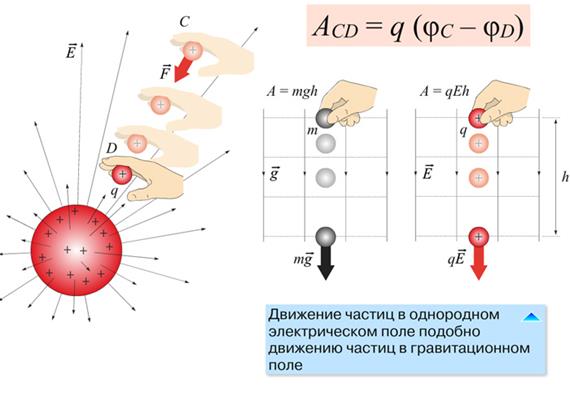Но к энергии взаимодействия применим другой подход. Можно сказать, что один заряд находится в электрическом поле, созданном другим зарядом. И тогда появляется возможность ввести некую характеристику электрического поля, однозначно определяющую потенциальную энергию взаимодействия, подобно тому, как потенциальную энергию тела поднятого над землей в поле однородной гравитации определяет высота над некоторым нулевым уровнем.
Потенциал
Физическая скалярная величина, характеризующая энергетическое состояние поля и равная отношению потенциальной энергии к величине помещенного заряда называется потенциалом данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал - это характеристика электростатического поля.
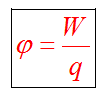
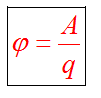
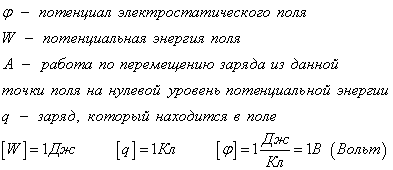
Нулевой уровень потенциальной энергии выбирают произвольно. Поэтому потенциал является относительной физической величиной. Потенциальная энергия поля - это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом. Обычно для точечного заряда нулевой потенциал выбирают на бесконечности. В однородном поле – произвольно, но для удобства целесообразно выбирать ноль в самой «дальней» по полю точке траектории заряда, тогда все значения потенциалов и потенциальной энергии будут положительными. Но это не обязательно.
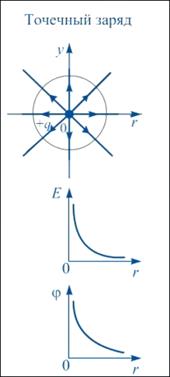
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.
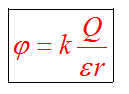
Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.
Разность потенциалов
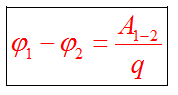
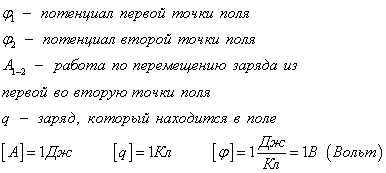Работа поля по перемещению заряда из одной точки в другую, определяется разностью потенциалов
Эту формулу можно представить в ином виде
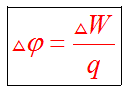
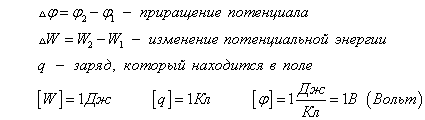
Для малых изменений потенциала верна формула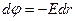 
, знак минус в ней подчеркивает, что потенциал убывает по полю.
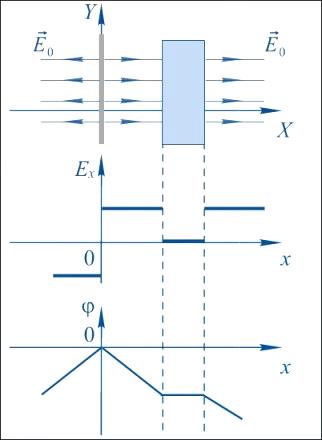
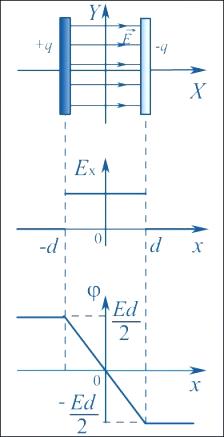
В случае однородного поля Разность потенциалов связана с напряженностью поля простым соотношением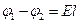 
, где l – проекция перемещения от 1 к 2 на направление вдоль силовых линий напряженности поля.
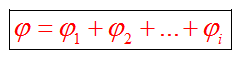Для потенциала (как и для напряженности) справедлив принцип суперпозиции, который отражает тот факт, что поля нескольких зарядов не искажают друг друга, а просто складываются. Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности
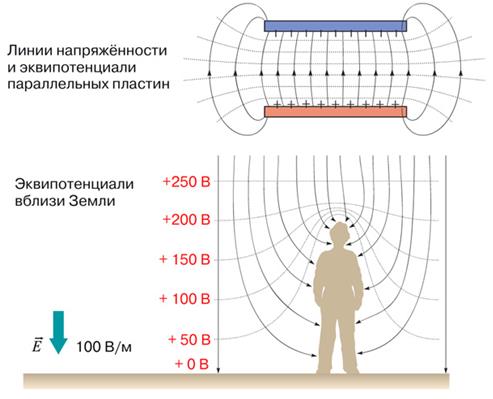
Зависимость напряженности и потенциала от расстояния
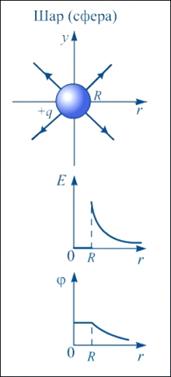
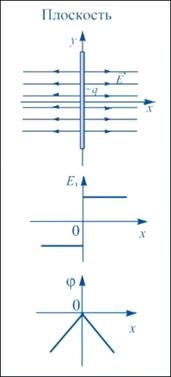
Геометрическое место точек, имеющих одинаковый потенциал, образует эквипотенциальную поверхность.
