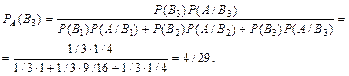Пусть B 1, B 2,…, Bn – попарно несовместные события (гипотезы) и А – событие, которое может произойти только совместно с одним из них.
Пусть, кроме того, нам известны Р (Bi) и Р (А / Bi) (i = 1, 2, …, n).
В этих условиях справедливы формулы:
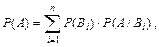 (1)
(1)
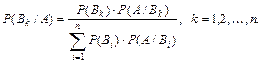 (2)
(2)
Формула (1) называется формулой полной вероятности. По ней вычисляется вероятность события А (полная вероятность).
Формула (2) называется формулой Байеса. Она позволяет произвести пересчет вероятностей гипотез, если событие А произошло.
При составлении примеров удобно считать, что гипотезы образуют полную группу.
Задача 1. В корзине яблоки с четырех деревьев одного сорта. С первого – 15% всех яблок, со второго – 35%, с третьего – 20%, с четвертого – 30%. Созревшие яблоки составляют соответственно 99%, 97%, 98%, 95%.
а) Какова вероятность того, что наугад взятое яблоко окажется спелым (событие А).
б) При условии, что наугад взятое яблоко оказалось спелым, вычислить вероятность того, что оно с первого дерева.
Решение. а) Имеем 4 гипотезы:
B1 – наугад взятое яблоко снято с 1-го дерева;
B2 – наугад взятое яблоко снято с 2-го дерева;
B3 – наугад взятое яблоко снято с 3-го дерева;
B4 – наугад взятое яблоко снято с 4-го дерева.
Их вероятности по условию: Р (B 1) = 0,15; Р (B 2) = 0,35; Р (B 3) = 0,2; Р (B 4) = 0,3.
Условные вероятности события А:
Р (А / B 1) = 0,99; Р (А / B 2) = 0,97; Р (А / B 3) = 0,98; Р (А / B 4) = 0,95.
Вероятность того, что наудачу взятое яблоко окажется спелым, находится по формуле полной вероятности:
Р (А)= Р (B 1)∙ Р (А / B 1)+ Р (B 2)∙ Р (А / B 2)+ Р (B 3)∙ Р (А / B 3)+ Р (B 4)∙ Р (А / B 4)=0,969.
б) Формула Байеса для нашего случая имеет вид:
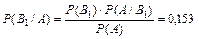 .
.
Задача 2. В урну, содержащую два шара, опущен белый шар, после чего из нее наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров (по цвету).
Решение. Обозначим через А событие – извлечен белый шар. Возможны следующие предположения (гипотезы) о первоначальном составе шаров: B1 – белых шаров нет, В2 – один белый шар, В3 – два белых шара.
Поскольку всего имеется три гипотезы, и сумма вероятностей гипотез равна 1 (так как они образуют полную группу событий), то вероятность каждой из гипотез равна 1/3,т.е.
P (B 1) = P (B 2) = P (B 3) = 1/3.
Условная вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне не было белых шаров, Р (А / B 1)=1/3. Условная вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне был один белый шар, Р (А / B 2)=2/3. Условная вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне было два белых шара Р (А / B 3)=3/3=1.
Искомую вероятность того, что будет извлечен белый шар, находим по формуле полной вероятности:
Р (А)= Р (B 1)∙ Р (А / B 1)+ Р (B 2)∙ Р (А / B 2)+ Р (B 3)∙ Р (А / B 3)=1/3·1/3+1/3·2/3+1/3·1=2/3.
Задача 3. Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй – 84%. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена первым автоматом.
Решение. Обозначим через А событие – деталь отличного качества. Можно сделать два предположения: B1 – деталь произведена первым автоматом, причем (поскольку первый автомат производит вдвое больше деталей, чем второй) Р (А / B 1) = 2/3; B 2 – деталь произведена вторым автоматом, причем P (B 2) = 1/3.
Условная вероятность того, что деталь будет отличного качества, если она произведена первым автоматом, Р (А / B 1)=0,6.
Условная вероятность того, что деталь будет отличного качества, если она произведена вторым автоматом, Р (А / B 1)=0,84.
Вероятность того, что наудачу взятая деталь окажется отличного качества, по формуле полной вероятности равна
Р (А)= Р (B 1)∙ Р (А / B 1)+ Р (B 2)∙ Р (А / B 2)=2/3·0,6+1/3·0,84 = 0,68.
Искомая вероятность того, что взятая отличная деталь произведена первым автоматом, по формуле Бейеса равна
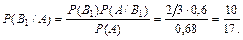
Задача 4. Имеются три партии деталей по 20 деталей в каждой. Число стандартных деталей в первой, второй и третьей партиях соответственно равны 20, 15, 10. Из выбранной партии наудачу извлечена деталь, оказавшаяся стандартной. Детали возвращают в партию и вторично из этой же партии наудачу извлекают деталь, которая также оказывается стандартной. Найти вероятность того, что детали были извлечены из третьей партии.
Решение. Обозначим через А событие – в каждом из двух испытаний (с возвращением) была извлечена стандартная деталь. Можно сделать три предположения (гипотезы): B 1 – детали извлекаются из первой партии, В 2– детали извлекаются из второй партии, В 3 – детали извлекаются из третьей партии.
Детали извлекались наудачу из взятой партии, поэтому вероятности гипотез одинаковы: P (B 1) = P (B 2) = P (B 3) = 1/3.
Найдем условную вероятность Р (А / B 1), т.е. вероятность того, что из первой партии будут последовательно извлечены две стандартные детали. Это событие достоверно, т.к. в первой партии все детали стандартны, поэтому Р (А / B 1) = 1.
Найдем условную вероятность Р (А / B 2), т.е. вероятность того, что из второй партии будут последовательно извлечены (с возвращением) две стандартные детали: Р (А / B 2)= 15/20 ∙ 15/20 = 9/16.
Найдем условную вероятность Р (А / B 3), т.е. вероятность того, что из третьей партии будут последовательно извлечены (с возвращением) две стандартные детали: Р (А / B 3) = 10/20 · 10/20 = 1/4.
Искомая вероятность того, что обе извлеченные стандартные детали взяты из третьей партии, по формуле Бейеса равна