Тема 2. Теоремы о вероятностях
2.1. Сумма и произведение событий. Основные теоремы теории вероятностей (сложения и умножения вероятностей). Полная группа событий.
Часто приходится работать не с одним случайным событием, а с несколькими. Для этих целей используют различные комбинации над событиями.
Теорема сложения вероятностей
Суммой, или объединением, нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий (в одном и том же испытании).
Сумма А 1 + А 2 + … + Аn обозначается так:
.
Пример 1. Событие А – выигрыш по 1 займу, событие В – выигрыш по 2 займу. Тогда событие А+В – выигрыш хотя бы по одному займу (возможно по двум сразу).
Произведением или пересечением нескольких событий называется событие, состоящее в совместном появлении всех этих событий (в одном и том же испытании).
Произведение В событий А 1, А 2, …, Аn обозначается так:
.
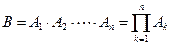Пример 2. События А и В состоят в успешном прохождении I и II туров соответственно при поступлении в институт. Тогда событие А×В состоит в успешном прохождении обоих туров.
Теорема. Если события Ai (i = 1, 2, …, n) попарно несовместны, то вероятность суммы событий равна сумме вероятностей этих событий:
.
Пусть А и Ā – противоположные события, т.е. А + Ā = W, где W – достоверное событие. Из теоремы сложения вытекает, что
Р(W) = Р (А) + Р (Ā) = 1, поэтому
Р (Ā) = 1 – Р (А).
Теорема. Если события А 1 и А 2 совместны, то вероятность суммы двух совместных событий равна:
Р (А 1 + А 2) = Р (А 1) + Р (А 2) – Р(А 1× А 2).
Теоремы сложения вероятностей позволяют перейти от непосредственного подсчета вероятностей к определению вероятностей наступления сложных событий.
Задача. Стрелок производит один выстрел по мишени. Вероятность выбить 10 очков (событие А), 9 очков (событие В) и 8 очков (событие С) равны соответственно 0,11; 0,23; 0,17. Найти вероятность того, что при одном выстреле стрелок выбьет менее 8 очков (событие D).
|
|
Решение. Перейдем к противоположному событию 
– при одном выстреле стрелок выбьет не менее 8 очков. Событие наступает, если произойдет А или В, или С, т.е. 
. Так как события А, В, С попарно несовместны, то, по теореме сложения,
, откуда 
.
Задача. От коллектива бригады, которая состоит из 6 мужчин и 4 женщин, на профсоюзную конференцию выбирается два человека. Какова вероятность, что среди выбранных хотя бы одна женщина (событие А).
Решение. Если произойдет событие А, то обязательно произойдет одно из следующих несовместных событий: В – «выбраны мужчина и женщина»; С – «выбраны две женщины». Поэтому можно записать: А=В+С. Найдем вероятность событий В и С. Два человека из 10 можно выбрать 
способами. Двух женщин из 4 можно выбрать 
способами. Мужчину и женщину можно выбрать 6×4 способами. Тогда 
. Так как события В и С несовместны, то, по теореме сложения,
Р (А) = Р (В + С) = Р (В) + Р (С) = 8/15 + 2/15 = 2/3.
Задача. На стеллаже в библиотеке в случайном порядке расставлено 15 учебников, причем пять из них в переплете. Библиотекарь берет наудачу три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете (событие А).
Решение. Первый способ. Требование – хотя бы один из трех взятых учебников в переплете – будет осуществлено, если произойдет любое из следующих трех несовместных событий: В – один учебник в переплете, С – два учебника в переплете, D – три учебника в переплете.
|
|
Интересующее нас событие А можно представить в виде суммы событий: A=B+C+D. По теореме сложения,
P(A) = P(B) + P(C) + P(D). (1)
Найдем вероятность событий B, C и D (см комбинаторные схемы):
Представив эти вероятности в равенство (1), окончательно получим
P(A) = 45/91 + 20/91 + 2/91 = 67/91.
Второй способ. Событие А (хотя бы один из взятых трех учебников имеет переплет) и Ā (ни один из взятых учебников не имеет переплета) – противоположные, поэтому P (A) + P (Ā) = 1 (сумма вероятностей двух противоположных событий равна 1). Отсюда P (A) = 1 – P (Ā). Вероятность появления события Ā (ни один из взятых учебников не имеет переплета)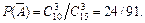 
Искомая вероятность
P (A) = 1 – P (Ā) = 1 – 24/91 = 67/91.