ЛАБОРАТОРНАЯ РАБОТА №11
ЦЕЛЬ РАБОТЫ: определить индуктивное и емкостное сопротивления, проверить закон Ома для переменного тока.
ПРИБОРЫИ ПРИНАДЛЕЖНОСТИ: источник переменного напряжения, дроссельная катушка, конденсаторы, реостат, миллиамперметры и вольтметры переменного тока, соединительные провода, ключ.
КРАТКАЯ ТЕОРИЯ
Закон Ома был установлен для постоянного тока, однако он остается справедливым и для мгновенных значений изменяющихся тока и напряжения, если только их изменения происходят не слишком быстро. Токи, удовлетворяющие такому условию, называются квазистационарными.
Переменный ток называется квазистационарным, если с достаточной степенью точности можно принять, что магнитное поле этого тока в каждый момент времени имеет те же значения, которые оно имеет в случае постоянного тока той же величины.
Процессы, протекающие в цепях переменного тока, несколько отличаются от процессов, наблюдаемых в цепях постоянного тока.
Если к участку цепи, содержащему только активное сопротивление R о, приложено переменное напряжение:
, (1)
где
U m - амплитуда напряжения;
w - циклическая частота,
то на этом участке возникает ток, мгновенное значение которого определяется соотношением:
, (2)
где
- амплитуда тока.
Уравнения (1) и (2) показывают, что фаза напряжения и тока одинакова, т.е. напряжение и ток одновременно достигают максимальных значений и одновременно обращаются в нуль.
Рассмотрим цепь переменного тока, которая содержит катушку с индуктивностью L и активным сопротивлением R (рис.1).
Переменная ЭДС E будет обусловливать синусоидальный ток:
. (3)
При протекании тока через катушку происходит падение напряжения на активном сопротивлении U R, а на концах катушки возникает ЭДС самоиндукции:
.
По второму закону Кирхгофа результирующее внешнее напряжение в цепи определяется суммой U R и EL, внешняя ЭДС записывается в следующей форме:
.
Дифференцируя это уравнение, получим:
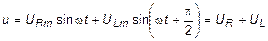, (4)
где
- амплитудное значение напряжения на активном сопротивлении;
- амплитудное значение напряжения на индуктивности.
Отсюда следует, что w L выполняет функцию сопротивления:
.
Величину X L называют реактивным сопротивлением.
Сравнивая выражения (3) и (4), видим, что в рассматриваемой цепи изменение тока отстает от изменения напряжения на угол 0,5p.
Физическая причина возникновения этой разности фаз заключается в следующем: если активное сопротивление участка цепи равно нулю, то приложенное напряжение в точности уравновешивает ЭДС самоиндукции и равно последней с обратным знаком. Но ЭДС самоиндукции пропорциональна не мгновенному значению тока, а быстроте его изменения, которая будет наибольшей в те моменты, когда ток проходит через нуль. Поэтому максимумы напряжения совпадают с нулями тока, и наоборот.
Соединим обкладки конденсатора, имеющего емкость C, к источнику переменного напряжения (рис. 2). Конденсатор начнет непрерывно перезаряжаться, и в цепи будет протекать переменный ток:
. (5)
Так как ток в подводящих проводниках равен:
,
то получим дифференциальное уравнение:
.
С учетом того, что в цепи отсутствует источник постоянного напряжения, решение данного уравнения имеет вид:
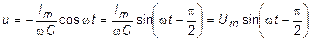, (6)
где
- амплитудное значение напряжения на конденсаторе.
Величина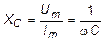 
называется емкостным сопротивлением. В отличие от активного сопротивления, емкостное сопротивление в среднем не потребляет мощности, так как конденсатор то забирает энергию из цепи при зарядке, то отдает ее обратно в цепь при разрядке.
Сравнивая выражения (5) и (6), видим, что фаза тока опережает фазу напряжения на 0,5p.
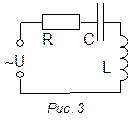Появление разности фаз j=0,5p между напряжением на обкладках конденсатора и током через него связано с процессами зарядки и разрядки конденсатора. Если ток равен нулю при полностью заряженном конденсаторе, то на конденсаторе имеется заряд, перенесенный током в предыдущий период времени, и напряжение на его обкладках достигает наибольшей величины. Когда же заряд конденсатора и, следовательно, напряжение станет равным нулю, ток имеет максимальное значение.
Если на участке активного сопротивления R o последовательно с ним включены катушка с индуктивностью L и конденсатор с емкостью С (рис. 3), то между током и напряжением возникает сдвиг фаз, мгновенное значение тока будет выражено соотношением:
, (7)
где
,
.
Отношение амплитуды напряжения к амплитуде тока называют полным сопротивлением цепи для переменного тока:
, (8)
где
R 0 - активное сопротивление,
- реактивное сопротивление цепи.
Приборы, которыми пользуются в цепях переменного тока, измеряют действующее значение тока и напряжения, но так как:
; 
, 
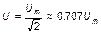(9)
то очевидно, что между действующими значениями тока и напряжения сохраняется то же соотношение, что между амплитудными:
.
ход РАБОТЫ