Начальные понятия
| Окружность | – геометрическая фигура, состоящая из всех точек плоскости, находящихся на заданном расстоянии от данной точки этой плоскости. Данная точка называется центром окружности |
| Радиус окружности | – отрезок, соединяющий центр окружности с какой-либо точкой этой окружности |
| Хорда окружности | – отрезок, соединяющий две точки окружности |
| Диаметр окружности | – хорда, проходящая через центр окружности |
| Дуга окружности | – каждая из частей окружности, на которые делят окружность любые две ее точки |
| Касательная к окружности | – прямая, имеющая с окружностью только одну общую точку. Эта точка называется точкой касания |
| Круг | – геометрическая фигура, состоящая из окружности и части плоскости, ограниченной этой окружностью |
| Круговой сектор | – часть круга, ограниченная двумя радиусами и дугой окружности |
| Круговой сегмент | – часть круга, ограниченная дугой окружности и хордой |
| Геометрическое тело | – ограниченная фигура в пространстве, обладающая следующими свойствами: 1) у нее есть внутренние точки, и любые две из них можно соединить ломаной, каждая точка которой является внутренней точкой фигуры; 2) фигура содержит свою границу и ее граница совпадает с границей ее внутренности. Граница тела называется его поверхностью |
2.1. Понятие тела вращения. Виды поверхностей и тел вращения
1) 
Пусть дана прямая l и точка M Ï l. Через точку M проведем плоскость a^ l, aÇ l = O. Рассмотрим окружность с центром в точке O и радиусом OM. О такой окружности говорят, что она получена в результате вращения точки M вокруг оси l.
2) 
Рассмотрим геометрическую фигуру F и прямую l. Каждой точке фигуры F поставим в соответствие окружность, полученную при вращении данной точки вокруг прямой l. Объединение всех таких окружностей называется фигурой вращения, полученной в результате вращения фигуры F вокруг прямой l, которая называется осью вращения.
Поверхность вращения - фигура вращения, образуемая при вращении произвольной линии (прямой, плоской или пространственной кривой) вокруг некоторой прямой
Тело вращения - фигура вращения, обладающая всеми свойствами геометрического тела
Виды поверхностей вращения
1) Цилиндрическая поверхность – результат вращения прямой, параллельной оси вращения.
2) Коническая поверхность – результат вращения прямой, не параллельной и не перпендикулярной оси вращения.
3) Сфера – результат вращения полуокружности вокруг прямой, содержащей диаметр.
Виды тел вращения
1) Цилиндр – результат вращения прямоугольника вокруг прямой, содержащей одну из его сторон.
2) Конус – результат вращения прямоугольного треугольника вокруг прямой, содержащей один из его катетов.
3) Шар – результат вращения полукруга вокруг прямой, содержащей диаметр.
2.2. Цилиндр. Боковая поверхность цилиндра. Объем цилиндра. Сечения цилиндра. Сечения цилиндрической поверхности
Можно выделить три подхода к определению понятия цилиндра:
 |  | ||
Через понятие тела вращения
Тело вращения –фигура вращения, обладающая всеми свойствами геометрического тела
| Через понятие цилиндрической поверхности
 В некоторой плоскости α рассмотрим окружность ω(O, R) с центром в точке О и радиуса R. Через каждую точку окружности ω(O, R) проведем прямую, перпендикулярную к плоскости α. Фигура, образованная этими прямыми, называется цилиндрической поверхностью, а сами прямые – образующими цилиндрической поверхности
| Через общее понятие цилиндра
 Рассмотрим фигуру F, лежащую в некоторой плоскости α и отрезок AA ¢, не лежащий в этой плоскости, A Îα. Из каждой точки X фигуры F проведем отрезок XX ¢, параллельный и равный отрезку AA ¢. Фигура, образованная всеми отрезками XX ¢, лежащими по одну сторону от плоскости α, называется цилиндром. Если AA ¢^α, то цилиндр называют прямым.
Фигуры F и F ¢(она состоит из концов отрезков XX ¢, не принадлежащих фигуре F) называются основаниями цилиндра. Если точка X отрезка XX ¢ принадлежит границе фигуры F, то отрезок XX ¢ называется образующей цилиндра.
Фигура, состоящая из всех образующих, называется боковой поверхностью цилиндра. Полной поверхностью цилиндра называется фигура, состоящая из боковой поверхности и двух его оснований
|
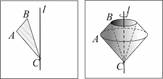
Цилиндр вращения (прямой круговой цилиндр) – тело вращения, полученное в результате вращения прямоугольника вокруг прямой, содержащей его сторону.
Пусть прямоугольник ABCD вращается вокруг прямой BC, тогда ломаная BADC описывает поверхность цилиндра, отрезок AD – его боковую поверхность, а отрезки AB и DC – его основания
| Прямой круговой цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя плоскостями, которые перпендикулярны образующим цилиндрической поверхности.
 Круги, отсекаемые цилиндрической поверхностью от этих плоскостей, называются основаниями цилиндра. Часть цилиндрической поверхности, которая расположена между этими плоскостями, называется боковой поверхностью цилиндра. Отрезки образующих цилиндрической поверхности, расположенные между плоскостями оснований цилиндра, называются образующими цилиндра. Прямая, проходящая через центры оснований цилиндра, называется осью цилиндра, длина его образующей – высотой цилиндра, а радиус его основания – радиусом цилиндра
| Прямой круговой цилиндр – цилиндр, основаниями которого являются круги, расположенные так, что их плоскости перпендикулярны прямой, проходящей через центры оснований.
 Прямая, проходящая через центры оснований цилиндра, называется осью прямого кругового цилиндра, радиусы кругов – радиусом прямого кругового цилиндра
|
Первый подход используется в учебном пособии Л.А. Латотина и Б.Д. Чеботаревского; второй – в учебных пособиях В.В. Шлыкова, Л.С. Атанасяна; третий подход – в учебных пособиях Н.М. Рогановского, А.Д. Александрова, а также пособии [3] Л.С. Атанасяна для студентов педагогических университетов и учащихся классов с углубленным изучением математики, в котором применяются термины «обобщенный цилиндр » (стр. 152), «обобщенный конус» (с.155).
В школе рассматриваются только прямые круговые цилиндры. Для краткости их называют цилиндрами.
Свойства цилиндра:
· Основания цилиндра лежат в параллельных плоскостях.
· Образующие цилиндра параллельны и равны между собой.
Теорема (о площади боковой поверхности цилиндра ) .
…
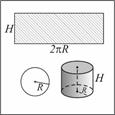
Иначе к этой формуле можно прийти, рассмотрев развертку боковой поверхности цилиндра:
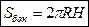
Теорема (об объеме цилиндра ) .
…
Сечения цилиндра плоскостью
При решении задач школьного курса геометрии рассматривают два вида сечений цилиндра плоскостью:
· 
сечения, перпендикулярные оси цилиндра – круги;
· сечения, параллельные оси цилиндра или проходящие через его ось – прямоугольники.
Сечение цилиндра плоскостью, проходящей через его ось, называется осевым сечением. Если осевым сечением цилиндра является квадрат, то цилиндр называют равносторонним.
Виды сечений цилиндрической поверхности плоскостью:
· сечение, перпендикулярное образующим – окружность;
· сечение, параллельное образующим – пара параллельных прямых;
· сечение, не перпендикулярное и не параллельное образующим – эллипс, т.е. множество точек плоскости, сумма расстояний от которых до двух заданных точек плоскости, называемых фокусами, есть величина постоянная.
Докажем это утверждение.
Утверждение 1. Сечение цилиндрической поверхности, не параллельное и не перпендикулярное образующей цилиндра – эллипс.
Пусть плоскость α, не параллельная и не перпендикулярная образующей цилиндра, пересекает поверхность цилиндра по некоторой линии l. Докажем, что эта линия – эллипс.
Рассмотрим два шара, которые касаются боковой поверхности цилиндра и плоскости α. Пусть точки F 1 и F 2 – точки касания. Через произвольную точку M линии l проведем образующую t. Пусть длина отрезка AA 1 этой образующей, заключенного между диаметральными плоскостями шаров, перпендикулярными образующим цилиндра, равна 2 a. Тогда по свойству касательных,
MF 1 = MA 1
+ MF 2 = MA
MF 1+ MF 2= MA 1+ MA = 2 a, т.е. MF 1+ MF 2 = const, значит, линия l – эллипс.Š
2.3. Конус. Боковая поверхность конуса. Объем конуса. Сечения конуса. Сечения конической поверхности
Можно выделить три подхода к определению понятия конуса:
 | |
Через понятие тела вращения
Тело вращения –фигура вращения, обладающая всеми свойствами геометрического тела
| Через понятие конической поверхности
 В некоторой плоскости α рассмотрим окружность ω(O, R) с центром в точке О радиуса R и прямую FO (F Ïα), которая перпендикулярна плоскости α. Через F и каждую точку окружности ω(O, R) проведем прямую. Фигура, образованная этими прямыми, называется конической поверхностью, сами прямые – образующими конической поверхности; прямая FO – осью конической поверхности.
| Через общее понятие конуса
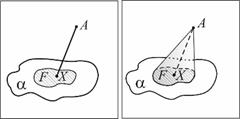 Рассмотрим фигуру F, лежащую в некоторой плоскости α и точку A вне этой плоскости. Из каждой точки X фигуры F проведем отрезок XA. Фигура, образованная всеми отрезками XA, называется конусом.
Фигура F называется основанием конуса, точка A – его вершиной.
Перпендикуляр, проведенный из вершины конуса к плоскости его основания, называется высотой конуса.
Если точка X отрезка AX принадлежит границе фигуры F, то отрезок AX называется образующей конуса.
Фигура, состоящая из всех образующих, называется боковой поверхностью конуса. Полной поверхностью конуса называется фигура, состоящая из боковой поверхности и его основания.
|
Конус вращения (прямой круговой конус) – тело вращения, полученное в результате вращения прямоугольного треугольника вокруг прямой, содержащей один из его катетов.
Пусть прямоугольный треугольник ABC вращается вокруг прямой AC, тогда ломаная ABC описывает поверхность конуса, отрезок AB – его боковую поверхность, а отрезок BC – его основание.
| Прямой круговой конус – геометрическое тело, ограниченное конической поверхностью и плоскостью, перпендикулярной оси этой поверхности.
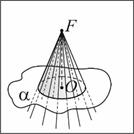 Круг, отсекаемый конической поверхностью от этой плоскости, называется основанием конуса, точка F – вершиной конуса. Отрезки конической поверхности, расположенные между вершиной и основанием конуса, называются образующими конуса. Фигура, образованная всеми образующими конуса, называется боковой поверхностью конуса. Прямая, проходящая через вершину и центр основания конуса, называется осью конуса, длина отрезка, концами которого служат вершина и центр основания конуса – высотой конуса, а радиус его основания – радиусом конуса.
| Прямым круговым конусом называют конус, основанием которого является круг, а высота проецируется в центр этого круга.
Прямая, проходящая через вершину и центр основания, называется осью прямого кругового конуса, радиус основания – радиусом прямого кругового конуса.
|
В школе рассматриваются только прямые круговые конусы. Для краткости их называют конусами.
Теорема (о площади боковой поверхности конуса ) .
…
Иначе к этой формуле можно прийти, рассмотрев развертку боковой поверхности конуса:
. Выразим угол α через радиус конуса и длину его образующей.
С одной стороны длина дуги сектора равна 
= 
. С другой стороны, она равна длине окружности основания конуса: 
. Из уравнения 
находим 
, тогда 
. 
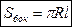
Теорема (об объеме конуса ) .
…
Сечения конуса плоскостью
При решении задач школьного курса геометрии рассматривают два вида сечений конуса плоскостью:
· сечения, перпендикулярные оси конуса – круги;
· сечения, проходящие через вершину конуса – равнобедренные треугольники;
Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением.
Виды сечений конической поверхности плоскостью:
· сечение, перпендикулярное оси конической поверхности – окружность;
· сечение, параллельное одной из образующих – парабола т.е. ________________________________
__________________________________________________________________________;
· сечение, параллельное двум образующим – гипербола, т.е. множество точек плоскости, модуль разности расстояний от которых до двух заданных точек плоскости есть величина постоянная.
· сечение, не параллельное образующим, не перпендикулярное и не параллельное оси конической поверхности – эллипс.
· сечение, проходящее через две образующие – пара пересекающихся прямых;
Докажем два утверждения.
Утверждение 2. Сечение конической поверхности, параллельное двум образующим конуса – гипербола.
Пусть плоскость α, параллельная двум образующим конуса, пересекает поверхность конуса по некоторой линии l. Докажем, что эта линия – гипербола.
Рассмотрим два равных шара, которые касаются боковой поверхности конуса и плоскости сечения. Пусть точки F 1 и F 2 – точки касания с плоскостью сечения. Через произвольную точку M линии l проведем образующую t. Пусть длина отрезка AA 1 этой образующей, заключенного между диаметральными плоскостями шаров, перпендикулярными образующим конуса, равна 2 a. Тогда по свойству касательных, MF 1= MA 1, MF 2 = MA 2, следовательно, | MF 1– MF 2|=| MA 1– MA 2=2 a |, т.е. | MF 1– MF 2| = const, значит, линия l – гипербола.Š
Утверждение 3. Сечение конической поверхности, не перпендикулярное и не параллельное оси конической поверхности – эллипс.
Сделать чертеж и доказать самостоятельно.
2.4. Усеченный конус
Усеченным конусом называется часть конуса, расположенная между его основанием и секущей плоскостью, перпендикулярной оси конуса. Основание данного конуса и круг, полученный в сечении, называются основаниями усеченного конуса. Высотой усеченного конуса называется отрезок, соединяющий центры его оснований; боковой поверхностью – часть конической поверхности, расположенная между основаниями усеченного конуса. Отрезки образующих конической поверхности, расположенные между основаниями усеченного конуса называются его образующими.
Усеченный конус может быть получен путем вращения прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной к основаниям.
Теорема (о площади боковой поверхности усеченного конуса ). Площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на длину образующей: 
, где R и r – радиусы оснований, l – длина образующей.
…
Теорема (об объеме усеченного конуса ). Объем усеченного конуса, высота которого равна H, а радиусы оснований равны R и r, вычисляется по формуле 
.
…
Сфера и шар
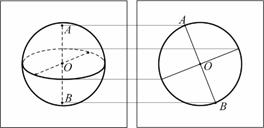
| Сфера –поверхность, образованная при повороте полуокружности вокруг прямой, содержащей диаметр, проходящий через концы этой полуокружности. | Сфера –множество всех точек пространства, находящихся на данном расстоянии от данной точки. Данная точка называется центром сферы, данное расстояние – радиусом сферы. |
Шар –геометрическое тело, образованное при повороте полукруга вокруг прямой, содержащей диаметр полукруга, принадлежащий его границе.
| Шар –множество всех точек пространства, находящихся от данной точки на расстоянии не больше данного.
|
Теорема (о взаимном расположении сферы и плоскости). Пусть d – расстояние от центра O сферы радиуса r до плоскости α. Тогда:
1) если d < r, то сечение сферы плоскостью α есть окружность с центром O 1 радиуса 
, где O 1 – проекция точки O на плоскость α;
2) если d = r, то сфера и плоскость имеют только одну общую точку;
3) если d > r, то сфера и плоскость не имеют общих точек.
1) Пусть d < r, плоскость a пересекает сферу W(O, r) по какой-то лини L. Пусть точка M – произвольная точка линии L, тогда в треугольнике OO 1 M:
Ð OO 1 M =90° (OO 1^ MO 1, т.к. OO 1^a и MO 1Ìa), катет MO 1= 
. Значит, все точки линии L равноудалены от точки O 1, следовательно, сечение сферы плоскостью a есть окружность с центром в точке O 1 и радиусом .
2) Пусть d = r. Расстояние от точки O до плоскости a меньше расстояния от точки O до любой точки плоскости a, отличной от точки O 1, значит, точка O 1 – единственная точка плоскости a, принадлежащая сфере.
3) Пусть d > r. Расстояние от точки O до любой точки плоскости a, отличной от точки O 1, больше d. А d > r, значит, сфера и плоскость не имеют общих точек.Š
Следствие. Сечение шара плоскостью есть круг.
Плоскость, проходящая через центр сферы (шара), называется диаметральной плоскостью, а сечение этой плоскостью – большой окружностью (большим кругом). Концы диаметра, перпендикулярного диаметральной плоскости, называются полюсами сферы.
Касательной плоскостью к сфере (шару) называется плоскость, имеющая со сферой (шаром) только одну общую точку. Она называется точкой касания. Прямая, лежащая в касательной плоскости сферы (шара) и проходящая через точку касания, называется касательной прямой к сфере (шару).
Теорема (признак касательной плоскости)
…
Теорема (о свойстве касательной плоскости)
…
Сферическим (шаровым) сегментом называется часть сферы (шара), отсекаемая плоскостью. Окружность (круг), по которой плоскость пересекает сферу (шар), называется основанием сферических (шаровых) сегментов, на которые плоскость разбивает сферу. Высотой сферического (шарового) сегмента называется длина отрезка диаметра, перпендикулярного основанию сегмента, расположенного между этим основанием и сферой. (На рисунке AF и BF – высоты соответствующих сферических (шаровых) сегментов).
Сферическим поясом (шаровым слоем) называется часть сферы (шара), расположенная между двумя параллельными секущими плоскостями. Основаниями сферического пояса (шарового слоя) называются окружности (круги), которые получаются в сечении сферы (шара) этими плоскостями. Высотой сферического пояса (шарового слоя) называется расстояние между плоскостями. (На рисунке FE – высота сферического пояса (шарового слоя).)
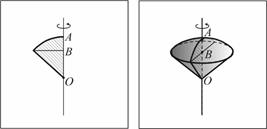Шаровым сектором называется геометрическое тело, полученное вращением кругового сектора с углом, меньшим 90°, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов. Шаровой сектор состоит из шарового сегмента и конуса. Высотой шарового сектора называется высота соответствующего ему шарового сегмента. (На рисунке AB – высота шарового сектора).
Уникальность сферической поверхности заключатся в отсутствии плоской развертки. Отсюда проблемы с вычислением площади этой поверхности элементарными средствами. Перечисленные ниже формулы доказываются средствами математического анализа.
Площадь сферического сегмента 
, где R – радиус сферы, h – высота сегмента.
Площадь сферического пояса 
, где R – радиус сферы, h – высота пояса.
Площадь сферы 
, где R – радиус сферы.
Объем шарового сектора 
, где R – радиус шара, h – высота сектора.
Объем шарового сегмента 
, где R – радиус шара, h – высота сегмента.
Объем шара 
, где R – радиус шара.