Возьмем наборы, на которых значение функции равно единице. Из переменных каждого такого набора составим конъюнкцию. Если значение переменной в наборе равно 0, заменим ее соотношением  , если 1, оставим без изменения. Между полученными таким образом выражениями возьмем сложение по модулю два. Раскроим скобки, применив дистрибутивный закон:
, если 1, оставим без изменения. Между полученными таким образом выражениями возьмем сложение по модулю два. Раскроим скобки, применив дистрибутивный закон: 
Это может быть, например, выражение вида:
 .
.
И приведем подобные члены с учетом соотношения:

Построим полином Жегалкина для функции  из предыдущего примера, заданной таблицей истинности.
из предыдущего примера, заданной таблицей истинности.
Имеем:

Получили полином третьей степени, поскольку максимальное число переменных в элементарных конъюнкциях в нашем случае, равно 3 - xyz.
Можно строить полином, используя СДНФ функции.
Классы булевых функций. Полные системы булевых функций.
Рассмотрим пять специальных классов (множеств) булевых функций, называемых также классами Поста. Эти классы обладают свойством функциональной замкнутости: любая булева функция, полученная с помощью операций суперпозиций из функций данного класса, принадлежит этому же классу.
Перечислим эти классы.
Класс (множество) булевых функций, сохраняющих нуль (константу нуль). Обозначается как  . Булева функция называется функцией, сохраняющей нуль, если на нулевом наборе переменных значение функция равна 0, т.е. f(00…0) = 0.
. Булева функция называется функцией, сохраняющей нуль, если на нулевом наборе переменных значение функция равна 0, т.е. f(00…0) = 0.
Класс булевых функций, сохраняющих единицу (константу единицу). Обозначается как 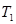 . Булева функция называется функцией, сохраняющей единицу, если на единичном наборе переменных значение функция равно 1, т.е. f(11…1) = 1.
. Булева функция называется функцией, сохраняющей единицу, если на единичном наборе переменных значение функция равно 1, т.е. f(11…1) = 1.
Класс линейных булевых функций. Обозначается через L. Булева функция называется линейной, если она может быть представлена полиномом степени не выше первой, т.е. представлена в виде:

где  - коэффициенты, равные 0 или 1.
- коэффициенты, равные 0 или 1.
Класс монотонных булевых функций. Обозначается через M.
Булева функция называется монотонной, если для любых двух сравнимых наборов a и b выполняется условие:
 .
.
Рассмотрим множество двоичных наборов функции n переменных. На этом множестве введем отношение сравнимости двоичных наборов следующим образом. Говорят, что двоичный набор  не больше двоичного набора
не больше двоичного набора  , обозначается
, обозначается  , если для каждой пары
, если для каждой пары  справедливо соотношение:
справедливо соотношение:  . Отношение сравнимости является отношением частичного порядка.
. Отношение сравнимости является отношением частичного порядка.
Для функции двух переменных следующие наборы сравнимы: 11 > 10, 11 > 01, 10 > 00 и т.д. Наборы 01 и 10 несравнимы, поскольку  , но
, но  . Таким образом, условие монотонности для функции двух переменных мы можем записать в виде:
. Таким образом, условие монотонности для функции двух переменных мы можем записать в виде:  .
.
Для функции трех переменных наборы 111 и 110, 101 и 001 являются сравнимыми. Наборы 110 и 001, 101 и 011 - несравнимы. Например, для последней пары наборов имеем:  ,
,  и
и  , а отношение
, а отношение  должно выполняться по всем переменным наборов.
должно выполняться по всем переменным наборов.
Множество двоичных наборов функции n переменных вместе с заданным на нем отношением сравнимости образует ЧУ - множество. Диаграмма Хассе для него при n = 3 приведена ниже на рисунке 1.

Рис. 1.
Для того, чтобы убедиться в немонотонности заданной булевой функции, достаточно найти хотя бы одну пару сравнимых наборов a и b, таких, что и f(a) > f(b).
и f(a) > f(b).
Чтобы сказать, что заданная булева функция монотонна, следует убедиться, что на всех сравнимых наборах выполняется условие монотонности .
.
Класс самодвойственных булевых функций. Обозначается через S.
Булева функция называется самодвойственной, если на каждой паре противоположенных наборов, она принимает противоположенные значения, т.е. если выполняется условие:
 .
.
Или, что то же самое:  .
.
Два набора переменных называются противоположенными, если все значения переменных одного набора противоположны значениям переменных другого набора. Чтобы получить противоположенный набор, инвертируем все значения переменных исходного набора.
Например, пары наборов 101 и 010, 011 и 100 – противоположенные.
Заданная функция не является самодвойственной, если найдется хотя бы одна пара противоположенных наборов, такая что выполняется условие  . Соответственно, функция самодвойственная, если на всех парах противоположенных наборов выполняется условие
. Соответственно, функция самодвойственная, если на всех парах противоположенных наборов выполняется условие  .
.
Зададим булеву функцию  таблицей истинности и проверим ее на принадлежность пяти классам Поста. Для нашей функции сначала выполняется импликация
таблицей истинности и проверим ее на принадлежность пяти классам Поста. Для нашей функции сначала выполняется импликация  , затем эквивалентность между значением x и результатом импликации.
, затем эквивалентность между значением x и результатом импликации.
| x | y | z | f(x, y, z) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
1. Функция сохраняет нуль, f(0,0,0) = 0.
2. Функция сохраняет единицу, f(1,1,1) = 1.
3. Построим для нашей функции полином Жегалкина:
 Получили полином второй степени, функция не является линейной.
Получили полином второй степени, функция не является линейной.
4. Она не является монотонной, поскольку f(0,1,1) < f(0,1,0) (набор больше, значение функции меньше).
5. Функция не самодвойственная, поскольку f(0,0,1) = f(1,1,0) (на противоположенных наборах значения функции равны).
Рассмотрим вопрос полноты системы булевых функций.
Система булевых функций  называется полной (функционально полной), если любая булева функция может быть выражена через функции системы
называется полной (функционально полной), если любая булева функция может быть выражена через функции системы  с помощью суперпозиций (т. е. составления сложных функций).
с помощью суперпозиций (т. е. составления сложных функций).
Мы уже сталкивались с полными системами при построении СДНФ, СКНФ, полинома Жегалкина для булевых функций.
СДНФ, СКНФ позволяют выразить любую булеву функцию через функции отрицания, конъюнкции и дизъюнкции. Имеем, система 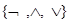 - полная система булевых функций.
- полная система булевых функций.
Полином Жегалкина позволяет выразить любую булеву функцию через функции сложение по модулю два, конъюнкцию и константу 1. Таким образом,система  - также является полной системой.
- также является полной системой.
Рассмотрим критерий построения полной системы, который дает теорема Поста.
Теорема Поста.
Для того, чтобы система булевых функций  была полной, необходимо и достаточно, чтобы для каждого из классов
была полной, необходимо и достаточно, чтобы для каждого из классов  ,
, 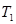 , L, M, и S нашлась функция
, L, M, и S нашлась функция  из системы, не принадлежащая этому классу.
из системы, не принадлежащая этому классу.
Построим еще полные системы булевых функций. Для этого составим таблицу Поста, где в строках укажем наиболее важные элементарные функции, а в столбцах - классы. В клетках таблицы будем ставить знаки «+ » или «- » в зависимости от того, принадлежит ли рассматриваемая функция данному функционально замкнутому классу или нет. В силу теоремы Поста для полноты рассматриваемой системы необходимо и достаточно, чтобы для системы в каждом столбце был хотя бы один минус.
Таблица Поста.
| Функции | Классы | ||||

| 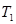
| L | M | S | |
| Константа 0 | + | - | + | + | - |
| Конъюнкция | + | + | - | + | - |
| Сложение по модулю два | + | - | + | - | - |
| Дизъюнкция | + | + | - | + | - |
| Стрелка Пирса | - | - | - | - | - |
| Эквивалентность | - | + | + | - | - |
| Импликация от x к y | - | + | - | - | - |
| Штрих Шеффера | - | - | - | - | - |
| Константа 1 | - | + | + | + | - |
| Инверсия x | - | - | + | - | + |
Найдем из таблицы полные системы булевых функций.
1. Одна функция, стрелка Пирса,  является полной системой.
является полной системой.
2. Штрих Шеффера,  также пример полной системы.
также пример полной системы.
3. Импликация от x к y,  и инверсия x,
и инверсия x,  - полная система.
- полная система.
4. Конъюнкция,  и инверсия x.
и инверсия x.
5. Дизъюнкция  и инверсия x.
и инверсия x.
Как видим из таблицы, система функций  является избыточной, нам бы хватило системы
является избыточной, нам бы хватило системы  или
или  . Полная система булевых функций называется базисом, если при удалении любой функции из этой системы, она перестает быть полной. Очевидно, полные системы
. Полная система булевых функций называется базисом, если при удалении любой функции из этой системы, она перестает быть полной. Очевидно, полные системы  ,
,  ,
,  являются базисами.
являются базисами.
Полная система  получила наибольшее практическое применение, и логическая часть ПК реализована, в основном, через функции этой системы. Эта система получила название основной функционально полной системы булевых функций, сокращенно ОФПС.
получила наибольшее практическое применение, и логическая часть ПК реализована, в основном, через функции этой системы. Эта система получила название основной функционально полной системы булевых функций, сокращенно ОФПС.