В общем случае существует несколько способов записи одной и той же булевой функции. Сложность записи булевой функции можно оценивать числом элементарных операций, используемых в такой записи и образующих функционально полную систему булевых функций.
Задачу поиска наиболее простой записи булевой функции называют задачей минимизации. Такая задача возникает в ряде приложений. В частности, при проектировании устройств автоматики или вычислительных устройств их работа может быть описана некоторой булевой функцией или системой таких функций. Каждой элементарной функции в устройствах соответствует некоторый физический элемент (ячейка), реализующий эту функцию. И, следовательно, представлению булевой функции в минимальной форме соответствует более простое устройство автоматики или вычислительной техники по сравнению с устройством, реализующим не минимальную булеву функцию.
Наиболее распространённой формой представления булевой функции является дизъюнктивная нормальная форма. Поэтому задачу упрощения булевых функций обычно формулируют в классе ДНФ.
ДНФ булевой функции  называют минимальной, если ей соответствует наименьший суммарный ранг R по сравнению с другими ДНФ этой же функции. Минимальную ДНФ булевой функции будем обозначать как МДНФ.
называют минимальной, если ей соответствует наименьший суммарный ранг R по сравнению с другими ДНФ этой же функции. Минимальную ДНФ булевой функции будем обозначать как МДНФ.
Поскольку методы минимизации булевых функций, разработанные для ДНФ, достаточно легко переносятся на конъюнктивные нормальные формы (КНФ), ограничимся рассмотрением методов минимизации в классе ДНФ.
В основном эти методы в явной или в неявной форме основаны на выполнении трех операций. Рассмотрим эти операции.
Две элементарных конъюнкции одинакового ранга r называются соседними, если они являются функциями одних и тех же переменных и отличаются только знаком отрицания одной из переменных.
Например, следующие элементарные конъюнкции являются соседними:
 и
и 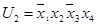 .
.
Первая операция, называемая операцией склеивания,для элементарных конъюнкций осуществляется по следующему правилу: дизъюнкцию двух соседних конъюнкций некоторого ранга r можно заменить одной элементарной конъюнкций ранга r-1, являющейся общей частью исходных конъюнкций.
 ,
,
где A – некоторая элементарная конъюнкция. В этом случае говорят, что конъюнкции  и
и  склеиваются по переменной x. Например:
склеиваются по переменной x. Например:
 .
.
Здесь  и две заданные конъюнкции были склеены по переменной
и две заданные конъюнкции были склеены по переменной 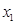 , в одной из которых эта переменная без отрицания, а в другой – с отрицанием.
, в одной из которых эта переменная без отрицания, а в другой – с отрицанием.
Вторая из операций называется операцией поглощения, и она осуществляется по правилу:
Дизъюнкцию двух элементарных конъюнкций разных рангов, из которых одна является собственной частью другой, можно заменить конъюнкцией, имеющим меньший ранг.
 ,
,
где А и В – некоторые элементарные конъюнкции.
Например,
 .
.
Третья операция – операция неполного склеивания:
 .
.
Введем некоторые понятия.
Булева функция  называется импликантой функции
называется импликантой функции  , если функция
, если функция 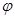 равна нулю на всех тех же наборах, на которых равна нулю и функция f. Если
равна нулю на всех тех же наборах, на которых равна нулю и функция f. Если 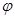
 есть импликанта функции f, то этот факт записывают следующим образом:
есть импликанта функции f, то этот факт записывают следующим образом:  .
.
Рассмотрим импликанты функции 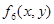 .
.
| x | y | 
| 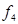
| 
| 
| 
|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 |
Как видим из таблицы, функции 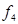 ,
,  ,
,  , являются импликантами функции
, являются импликантами функции  , функция
, функция  - нет. Термин «импликанта» возник ввиду того, что импликация
- нет. Термин «импликанта» возник ввиду того, что импликация  значений функций
значений функций 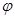 и
и  по всем наборам тождественно равна единице.
по всем наборам тождественно равна единице.
Конституента единицы в СДНФ функции f всегда является её импликантой. Для функции  функции
функции 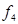 и
и  являются конституентами елиницы из ее СДНФ.
являются конституентами елиницы из ее СДНФ.
Из определения импликанты 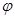 следует, что если на некотором наборе значение
следует, что если на некотором наборе значение  равно единице, то и значение функции f на этом же наборе также равно единице и в этом случае говорят, что импликанта
равно единице, то и значение функции f на этом же наборе также равно единице и в этом случае говорят, что импликанта 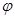 покрывает единицу функции f.
покрывает единицу функции f.
Чем меньше переменных содержит импликанта функции f по сравнению с конституентой единицы из ее СДНФ, тем больше единиц функции она покрывает.
Элементарная конъюнкция  называется простой импликантой булевой функции
называется простой импликантой булевой функции  , если U является импликантой функции f и никакая собственная часть U не является импликантой f.
, если U является импликантой функции f и никакая собственная часть U не является импликантой f.
Рассмотрим пример. Зададим функция f(x, y, z) таблицей истинност. (таблица ниже). СДНФ функции имеет вид:
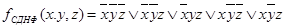 .
.
Укажем импликанты и простые импликанты нашей функции.
| x | y | z | f(x, y, z) | 
| 
| 
| 
| 
|
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
Как видим из таблицы, конституента единицы  является импликантой нашей функции, ее собственная часть
является импликантой нашей функции, ее собственная часть  - простой импликантой, поскольку ни
- простой импликантой, поскольку ни  , ни
, ни 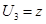 не являются импликантами. Аналогично имеем,
не являются импликантами. Аналогично имеем,  ,
,  - импликанты нашей функции,
- импликанты нашей функции, 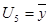 - простая импликанта;
- простая импликанта;  покрывает 4 единицы нашей функции. Простые импликанты в таблице выделены серым цветом.
покрывает 4 единицы нашей функции. Простые импликанты в таблице выделены серым цветом.
Справедливы следующие теоремы.
Теорема 1.
Всякая булева функция  может быть представлена как дизъюнкция всех своих простых импликант.
может быть представлена как дизъюнкция всех своих простых импликант.
Дизъюнкция всех простых импликант функции f называется сокращённой ДНФ этой функции. Сокращённая ДНФ булевой функции единственна.
Теорема 2. (теорема Квайна).
Если в совершенной дизъюнктивной нормальной форме булевой функции выполнить все операции неполного склеивания, а затем все операции поглощения, то в результате будет получена сокращенная дизъюнкти вная нормальная форма этой функции, или дизъюнкция всех ее простых импликант.
Как следует из теоремы, чтобы получить все простые импликанты, мы проводим операции неполного склеивания. Это связано с тем, что одна и та же элементарная конъюнкция дизъюнктивной формы может склеиваться с несколькими конъюнкциями. При каждом таком склеивании образуются различные импликанты и, поэтому мы оставляем в выражении каждую элементарную конъюнкцию для использования ее при других склеиваниях.
От сокращенной ДНФ переходим к минимальной дизъюнктивной нормальной форме – МДНФ.
Рассмотрим один из методов минимизации булевых функций
Метод Квайна.
Этот метод удобен для нахождения МДНФ функции от любого числа переменных.
Алгоритм метода Квайна.
1. Записываем СДНФ булевой функции  .
.
2. Проводим все возможные операции неполного склеивания конституент единицы СДНФ булевой функции, в результате операций получим элементарные конъюнкции ранга (n – 1). Проводим, если это возможно, операции поглощения между конъюнкциями различных рангов. Затем вновь проводим операции неполного склеивания и поглощения до тех пор, пока это возможно. Элементарная конъюнкция, которая не может больше участвовать в склеивании, является простой импликантой булевой функции.
3. Дизъюнкция простых импликант приводит к сокращённой ДНФ булевой функции:  , где
, где 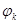 − простая импликанта.
− простая импликанта.
4. Строим таблицу покрытия (импликантную матрицу). Таблица покрытия − двумерная таблица, каждой строке которой взаимно однозначно соответствует простая импликанта, а каждому столбцу – конституента единицы из заданной СДНФ. На пересечении i-ой строки и j-го столбца находится 1 (можно ставить «крестик»), если простая импликанта является собственной частью соответствующей конституенты единицы, т.е. каждая переменная, входящая в простую импликанту, входит и в конституенту.
5. Выбираем существенные импликанты, т.е. такое минимальное количество простых импликант, чтобы они совместно своими единицами покрывали все колонки импликантной матрицы.
6. Дизъюнкция существенных импликант приводит к МДНФ.
Рассмотрим пример. Найдем МДНФ булевой функции, заданной СДНФ:
 .
.
1. Проведем операции неполного склеивания, их лучше выполнять последовательно, слева на право.
 .
.
 .
.
 .
.
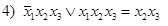 .
.
У нас все конституенты единицы участвовали в склеивании, поэтому операций поглощения нет. Элементарные конъюнкции больше не склеиваются между собой, следовательно, мы получили простые импликанты.
2. Из простых импликант строим сокращенную ДНФ функции:
 .
.
3. Строим таблицу покрытия
| Простые импликанты | Конституенты единицы | ||||

| 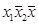
| 
| 
| 
| |

| 1 | 1 | 0 | 0 | 0 |

| 0 | 1 | 1 | 0 | 0 |

| 0 | 0 | 1 | 0 | 1 |

| 0 | 0 | 0 | 1 | 1 |
Выбираем существенные импликанты.
Первая импликанта входит в МДНФ обязательно, она единственная, кто покрывает единицу функции на наборе 000 (единственная единица в первой колонке), затем можно выбрать 3-ю и 4-ю простые импликанты. Получили МДНФ:
 .
.
У нашей функции две МДНФ: к первой импликанте можно выбрать 2-ю и 4-ю. Получим:
 .
.
Как видим, у булевой функции может быть несколько МДНФ.
Ранг обеих МДНФ, R = 6.
В тоже время, построив СКНФ заданной функции и проведя минимизацию методом Квайна в базисе КНФ, мы получим единственную МКНФ (минимальную конъюнктивную нормальную форму) меньшего ранга, R = 5.

 .
.
Рассмотрим еще пример.
 .
.
Проведем операции неполного склеивания.
1.  .
.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
Все конституенты единицы участвовали в склеивании, у нас нет операции поглощения. Импликанта  больше не участвует в склеивании, это простая импликанта. Оставшиеся импликанты могут склеиваться между собой, продолжим склеивание.
больше не участвует в склеивании, это простая импликанта. Оставшиеся импликанты могут склеиваться между собой, продолжим склеивание.
6.  .
.
7.  .
.
Операции поглощения у нас опять нет, получили 2 простые импликанты. Сокращенная ДНФ функции имеет вид:
 .
.
Построим таблицу покрытия.
| Простые импликанты | Конституенты единицы | ||||

| 
| 
| 
| 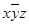
| |

| |||||

|
Обратите внимание, что простая импликанта  состоит только из отрицания одной переменной и покрывает 4 единицы нашей функции.
состоит только из отрицания одной переменной и покрывает 4 единицы нашей функции.
Как видим, обе простые импликанты входят МДНФ:
