СДНФ, СКНФ булевой функции. Полином Жегалкина.
Мы рассмотрели представление булевой функции через таблицу истинности. Решим обратную задачу: представим булеву функцию, заданную таблицей истинности, через элементарные функции.
Введем некоторые понятия, связанные с булевыми функциями.
Пусть имеется некоторый конечный набор переменных булевой функции:  Всякую конъюнкцию переменных функции, взятых с отрицанием или без отрицания, при этом каждая переменная встречается не более одного раза, называют элементарной. Например,
Всякую конъюнкцию переменных функции, взятых с отрицанием или без отрицания, при этом каждая переменная встречается не более одного раза, называют элементарной. Например,  - элементарная конъюнкция,
- элементарная конъюнкция,  - нет.
- нет.
Число r переменных в элементарной конъюнкции U называется ее рангом. Наша конъюнкция имеет ранг: r = 4. Константа единица считается элементарной конъюнкцией ранга 0.
Дизъюнкцию элементарных конъюнкций называют дизъюнктивной нормальной формой, сокращенно ДНФ.
Пусть булева функция задана через ДНФ:  , где
, где  - элементарные конъюнкции. Число s называют длиной ДНФ.
- элементарные конъюнкции. Число s называют длиной ДНФ.
ДНФ можно охарактеризовать также числом  , которое называют суммарным рангом этой ДНФ. Здесь
, которое называют суммарным рангом этой ДНФ. Здесь 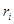 - ранг i – ой элементарной конъюнкции.
- ранг i – ой элементарной конъюнкции.
Например, для булевой функции  , ее суммарный ранг ее ДНФ, R = 5.
, ее суммарный ранг ее ДНФ, R = 5.
Пусть имеется элементарная конъюнкция  . Собственной частью конъюнкции U называют конъюнкцию, полученную из U, удалением из U некоторых переменных.
. Собственной частью конъюнкции U называют конъюнкцию, полученную из U, удалением из U некоторых переменных.
Например, если  , то собственными частями конъюнкции U являются, например, конъюнкции:
, то собственными частями конъюнкции U являются, например, конъюнкции: 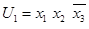 ,
,  ,
, 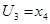 и т. д.
и т. д.
Аналогично вводится понятие и для элементарной дизъюнкции. Например,  - элементарная дизъюнкция ранга 4.
- элементарная дизъюнкция ранга 4.
Конституентой единицы называют булеву функцию n переменных, которая принимает значение, равное единице на одном единственном наборе переменных. Обозначается конституента единицы как 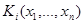 , где i - номер набора, на котором значение
, где i - номер набора, на котором значение  равно единице. Например,
равно единице. Например, 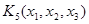 принимает значение 1 на единственном наборе - 101.
принимает значение 1 на единственном наборе - 101.
Как мы знаем, конъюнкция равна единице, если значения всех ее переменных равны единице, поэтому конституенту единицы можно выразить через конъюнкцию всех своих переменных. Для этого необходимо взять набор, на котором значение конституенты равно единице и из переменных набора и их отрицаний составить конъюнкцию. Причем, если значение переменной в наборе равно 1, берем ее без отрицания, если 0 - с отрицанием. Например,  .
.
Перейдем к СДНФ.
Дизъюнкция конституент единицы, равных единице на тех же наборах, что и заданная функция, называется совершенной дизъюнктивной нормальной формой булевой функции, сокращенно СДНФ.
Л юбую булеву функцию 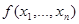 , кроме константы 0, можно представить в виде СДНФ и это представление единственно.
, кроме константы 0, можно представить в виде СДНФ и это представление единственно.
Как видим, любая булева функция может быть выражена через «базис» – конъюнкцию, д изъюнкцию и отрицание.
Чтобы получить совершенную дизъюнктивную нормальную форму (СДНФ), надо взять все наборы, на которых значение функции равно 1 и записать для каждого из них конъюнкцию переменных и их отрицаний. Если в наборе значение переменной равно 0 – то переменную надо взять с отрицанием, если 1 – без отрицания. Из получившихся конъюнкций надо построить дизъюнкцию.
Рассмотрим пример, построим СДНФ функции , заданной таблицей истинности.
, заданной таблицей истинности.
| x | y | z | f(x, y, z) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
СДНФ нашей функции имеет вид:
 .
.
Перейдем к СКНФ.
Конституентой нуля называют булеву функцию n переменных, которая принимает значение, равное нулю, на одном единственном наборе переменных.
Будем обозначать конституенту нуля как  , где i - номер набора, на котором значение
, где i - номер набора, на котором значение  равно нулю. Например, значение
равно нулю. Например, значение  равно 0 на единственном наборе - 101.
равно 0 на единственном наборе - 101.
Как мы знаем, дизъюнкция переменных равна нулю, если значения всех переменных равны нулю, поэтому конституенту нуля можно выразить через дизъюнкцию всех своих переменных следующим образом. Для этого необходимо взять набор, на котором значение конституенты  равно нулю и из переменных набора и их отрицаний составить дизъюнкцию. Причем, если значение переменной в наборе равно 0, берем ее без отрицания, если - 1, с отрицанием. Например,
равно нулю и из переменных набора и их отрицаний составить дизъюнкцию. Причем, если значение переменной в наборе равно 0, берем ее без отрицания, если - 1, с отрицанием. Например,  .
.
Конъюнкция конституент нуля, которые равны нулю на тех же наборах, что и заданная функция, называется совершенной конъюнктивной нормальной формой, сокращенно СКНФ.
Л юбую булеву функцию  , кроме константы 1, можно представить в виде СКНФ и это представление единственно.
, кроме константы 1, можно представить в виде СКНФ и это представление единственно.
СКНФ строится по следующему правилу:
Чтобы получить совершенную конъюнктивную нормальную форму, надо взять все наборы, на которых значение функции равно 0 и записать для каждого из них дизъюнкцию переменных и их отрицаний. Если в наборе значение переменной равно 0, то переменную надо взять без отрицания, если 1 – с отрицанием. Из получившихся дизъюнкций надо построить конъюнкцию.
Построим СКНФ функции  из предыдущего примера.
из предыдущего примера.
Имеем:
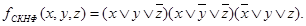
Перейдем к полиному Жегалкина.
Справедлива следующая теорема Жегалкина.
Любая булева функция может быть представлена в виде полинома, т.е. записана в форме:

где  -коэффициенты, равные нулю или единице.
-коэффициенты, равные нулю или единице.
Слагаемое отсутствует, если коэффициент при нем равен нулю. Как мы видим, полином Жегалкина строится с помощью операций: сложение по модулю два, конъюнкции и константы 1. Полином Жегалкина для каждой булевой функции единственен.
Максимальное число сомножителей в элементарных конъюнкциях, входящих в полином, называется степенью полинома.
Полином Жегалкина можно построить различными способами: используя таблицу истинности (через СДНФ), методом неопределенных коэффициентов, методом треугольника.