1. Сколькими способами можно выбрать комитет, включающий 6 мужчин и 8 женщин, из группы, состоящей из 12 мужчин и 20 женщин?
2. В скачках участвуют десять лошадей. Сколько существует вариантов призовой тройки лошадей?
Пять пар идут в кино. Сколькими способами они могут занять места, если
а) они могут сидеть в любом порядке? б) все пять пар сидят подряд?
3. Пароль на компьютере состоит из шести символов. Первые два из них строчные буквы латинского алфавита (всего 26 букв), а оставшиеся четыре могут быть как цифрами, так и строчными буквами. Сколько можно придумать различных паролей?
4. Комитет из 20 членов избирает председателя и секретаря. Сколькими способами это можно сделать?
5. Предстоит выбрать команду четырех игроков в гольф из пяти профессиональных игроков и пяти любителей. Сколько разных команд может состоять из трех профессионалов и одного любителя?
6. Сколько четырехзначных чисел, не превосходящих 6 000, можно составить, используя только нечетные цифры?
7. Имеются семь различимых шаров, и требуется положить три шара в первую коробку, два шара — во вторую и два шара — в третью коробку. Сколькими способами можно это сделать?
8. Предположим, что 12 книг, включающих 4 одинаковых учебника по математике, 6 одинаковых учебников по информатике, 2 одинаковых учебника по химии, следует расставить на полке. Сколькими способами это можно сделать?
9. Пусть задано множество А = {a, b, с, d, е, f, g, h}. Сколько существует а) трехэлементных подмножеств множества А? б) пятиэлементных подмножеств множества А, содержащих b? в) пятиэлементных подмножеств множества А, не содержащих b?
10. Сколько существует способов разделить 10 человек на две команды по 5 человек для игры в баскетбол?
11. Сколькими способами можно расставить в ряд для фотографирования пять мальчиков и шесть девочек, если ни две девочки, ни два мальчика не должны стоять рядом?
12. В зоомагазине продаются 5 черепах, 7 ящериц и 12 мышей. Сколько существует способов выбрать себе 2 черепахи, 3 ящерицы и 5 мышей?
ТЕМА №3. РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ.
Дадим определение последовательности. Если каждому натуральному числу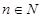 
поставлен в соответствие какой-то элемент 
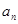из некоторого множества A,то говорят, что задана последовательность элементов множества A: 
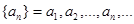Это могут быть последовательности чисел или элементов какого-то другого множества. Например, последовательность биномиальных коэффициентов 
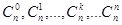при фиксированном значении числа n - пример конечной последовательности целых положительных чисел. Если мы знаем, как определяется элемент последовательности 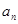при каждом значении 
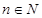, то такое задание последовательности называется явным. Например, значение биномиальных коэффициентов вычисляется по формуле: 
.
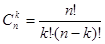Последовательность может быть описана неявно, рекурсивно – с помощью рекуррентного соотношения.
Последовательность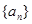 
называется рекуррентной порядка k (
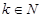), если существует формула 
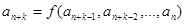, с помощью которой каждый последующий элемент последовательности 
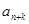вычисляется через предыдущие элементы 
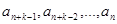. Данная формула называется рекуррентным соотношением порядка k. Заметим, что первые k элементов последовательности должны быть заданы.
Например, последовательность чисел Фибоначчи 0, 1, 1, 2, 3, 5, 8, 13,… задается рекуррентным соотношением 2 порядка, данную числовую последовательность мы обозначили как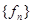 
:
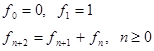(1)
Последовательность Фибоначчи является частным случаем линейных однородных рекуррентныхсоотношений с постоянными коэффициентами порядка k. В общем случае они имеют вид:
, 
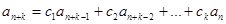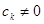, (2)
где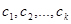 
- постоянные коэффициенты,
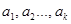– k начальных условий, (начальные значения последовательности 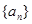). (2a)
Существует общий метод решения (т.е. отыскания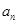 
как функции n) данных рекуррентных соотношений. Мы рассмотрим методику решения линейных однородных рекуррентныхсоотношений с постоянными коэффициентами порядка k на примере задачи Фибоначчи – (1).
Решение рекуррентного соотношения будем искать в виде:
.
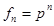Подставив это решение в рекуррентное соотношение (1), получим:
.
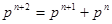Разделив обе части этого соотношения на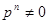 
,имеем:
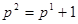
Или:
.
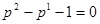Это уравнение называется характеристическим для данного рекуррентного соотношения. Решив квадратное уравнение, получим:
.
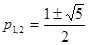Общее решение нашего рекуррентного соотношения имеет вид:
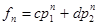, (3)
подставив в (3) корни характеристического уравнения, имеем:
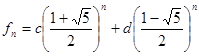
Решение рекуррентного соотношения k – го порядка называется общим, если оно зависит от k произвольных постоянных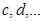 
и путем подбора этихпостоянных можно получить любое частное решение данного соотношения. Используем начальные условия для нахождения коэффициентов 
:
.
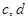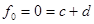
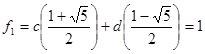Решая систему, находим:
.
, 
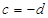
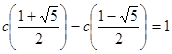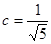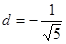
Подставив полученные коэффициенты в (3), получим решение рекуррентного соотношения (1) для последовательности чисел Фибоначчи.
,
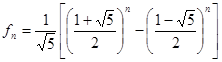формулу Бине для вычислений чисел Фибоначчи. Это выражение при всех натуральных значениях n принимает целые значения.
Рассмотрев ситуацию, когда характеристическое уравнение имело два различных действительных корня, перейдем к случаю кратных корней. В этом случае общее решение для рекуррентного соотношения 2-го порядка будет иметь вид:
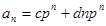. (4)
Рассмотрим пример, решим рекуррентное соотношение:
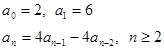
Характеристическое уравнение имеет вид:
.
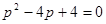Решая его, получаем кратный корень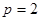 
.
Общее решение имеет вид:
.
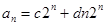Коэффициенты 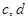найдем, исходя из начальных условий:
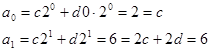
Отсюда получаем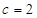 
, 
.
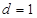Решение имеет вид:
.
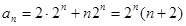Рассмотренные примеры позволяют изложить общий прием решения линейных однородных рекуррентныхсоотношений порядка k с постоянными коэффициентами. Рассмотрим рекуррентноесоотношение (2).
Будем предполагать, что характеристическое уравнение имеет простые корни. Решение соотношения ищем в виде: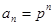 
.
Подставляя это выражение в (2) и разделив обе части на 
, получим полином k – степени:
.
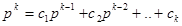Это уравнение имеет k корней: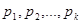 
. Тогда общее решение соотношения имеет вид:
.
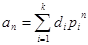Неизвестные коэффициенты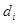 
находим, используя начальные условия (2a), которые позволяют составить систему линейных алгебраических уравнений относительно этих коэффициентов.
Последовательность биномиальных коэффициентов (числа сочетаний) можно также задать рекуррентным соотношением.
Приведем рекуррентное соотношение для числа сочетаний:
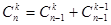. (5)
Докажем его следующими рассуждениями. Составим (n,k) -сочетания из элементов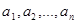 
некоторого множества A и разобьем их на два непересекающихся класса. Для этого зафиксируем некоторый элемент 
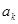. В первый класс войдут сочетания, содержащие элемент 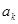, а во второй - сочетания, не содержащие этого элемента.
Рассмотрим первый класс. Т.к. один элемент, 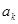, мы уже выбрали, то нам останется выбрать (k-1) элемент из (n-1) элемента.Число этих сочетаний равно 
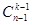. Поэтому в первый класс входит 
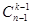комбинации.
Сочетания второго класса являются k -сочетаниями, составленными из (n- 1) элемента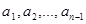 
. Поэтому их число равно 
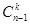. Поскольку любое
k -сочетание из элементов 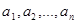, принадлежит одному и только одному из этих классов, а общее число этих сочетаний равно 
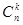, то приходим к равенству:
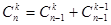
Полученное рекуррентное соотношение широко используется для вычисления числа сочетаний. На его основе составляется треугольник Паскаля
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
В этом треугольнике строкам соответствуют значения n = 0, n = 1, n = 2 и так далее, а диагоналям – значения k = 0, k = 1, k = 2 и так далее (сверху вниз и слева направо). Каждое число внутри треугольника Паскаля равно сумме двух чисел, расположенных над ним.
Так, чтобы вычислить значение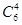 
с помощью треугольника Паскаля, необходимо по горизонтали выбрать 7 -ю строку и 5 -ю диагональ (нумерация начинается с 0). На пересечении имеем число 15, что и является значением искомого сочетания.
Легко видеть, что каждый элемент строки треугольника Паскаля вычисляется из элементов предыдущей строки, согласно найденному рекуррентному соотношению: .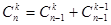
Легко заметить, что (n+1) -ый ряд состоит из коэффициентов разложения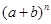 
. Например, при n = 5 имеем следующие коэффициенты в разложении: 1,5,10,10, 5,1.
При разложении степени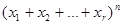 
коэффициенты при произведениях 
, 
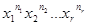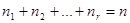, рассчитываются по формуле:
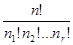(число перестановок с повторениями)
и носят название полиномиальных или мультиномиальных коэффициентов.
Например, вычислим коэффициент при произведении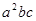 
в разложении
.
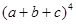Он равен: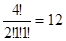 
.