1. Сколько четырехзначных чисел, не превосходящих 6 000, можно составить, используя только нечетные цифры?
2. Сколько существует целых чисел между 0 и 1000, содержащих ровно одну цифру 6?
3. Сколькими способами можно выбрать две книги по разным темам, когда на полке находятся 15 книг по информатике, 12 книг по математике и 10 книг по химии?
4. Сколько существует номерных знаков для автомобилей, состоящих из двух латинских букв и последующих четырех цифр?
5. Сколько положительных целых чисел, меньших 1001, делятся на 2, 3 или 5?
6. Пусть S — множество четырехзначных чисел, в чьей десятичной записи участвуют цифры: 0, 1, 2, 3, и 6, причем 0 на первом месте, естественно, стоять не может. Какова мощность множества S? Сколько чисел из S в своей десятичной записи не имеют повторяющихся цифр?
ТЕМА №2. КОМБИНАТОРНЫЕ КОНФИГУРАЦИИ.
Дадим понятие выборки.
Набор (комбинация) из k -элементов множества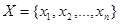 
мощности n называется выборкой объема k из n элементов или выборкой из n элементов по k, или просто (n,k) выборкой.
Выборка называется упорядоченной, если существенным является не только состав элементов в ней, но и порядок их расположения. Две упорядоченные выборки считаются различными, если они отличаются, либо составом элементов, либо порядком их расположения. Например, упорядоченные выборки (1,2) и (2,1) считаются различными, хотя и составлены из одних и тех же элементов.
Выборка называется неупорядоченной, если порядок следования элементов в ней не существенен. Так, соответственно, {1,2} и {2,1} считаются одной и той же неупорядоченной выборкой.
Как мы знаем, фигурные и круглые скобки подчёркивают отличие неупорядоченной выборки от упорядоченной.
В выборках могут допускаться или не допускаться повторение элементов. Выборка, в которой все элементы попарно различны, называется выборкой без повторений, в отличие от выборки с повторениями, в которую могут входить одинаковые элементы.
В зависимости от указанных свойств, выборки носят специальные названия.
· (n,k)-размещением с повторениями называется упорядоченная (n,k) выборка, элементы в которой могут повторяться;
· (n,k)-размещением без повторений называется упорядоченная (n,k) выборка, элементы которой попарно различны;
· (n,k)-сочетанием с повторениями называется неупорядоченная (n,k) выборка, элементы которой могут повторяться;
· (n,k)-сочетанием без повторений называется неупорядоченная (n,k) выборка, элементы которой попарно различны.
Рассмотрим пример, составим всевозможные (3,2)- выборки из элементов множества M = {a,b,c}.
1. (a,a), (a,b), (a,c), (b,b), (b,a), (b,c), (c,c), (c,a), (c,b) – это размещения с повторениями. Их всего 9.
2. (a,b), (b,a), (a,c), (c,a), (b,c), (c,b) – это размещения без повторений. Их, очевидно, всего 6.
3. (a,b), (a,a), (a,c), (b,b), (b,c), (c,c) - сочетания с повторениями. Их всего 6.
4. (a,b), (a,c), (b,c) – сочетания без повторений. Их всего 3.
При решении комбинаторных задач, в которых требуется определить количество некоторых выборок (конфигураций) из данного множества элементов, основным моментом является правильное определение характера выборок - упорядоченные это выборки или нет, с повторениями или без повторений.
Найдем чему равно количество различных комбинаторных конфигураций.
Число (n,k)-размещений с повторениями обозначается, как 
ивычисляется по формуле:
, 
.
Полученную формулу мы можем получить следующими рассуждениями.
На первое место выборки мы можем поставить любой из n элементов множества, т.е. у нас n способов выбора первого элемента. Поскольку повторения разрешены, то на второе место мы опять можем поставить любой элемент из того же множества и так далее, вплоть до места с номером k, выбрать который мы можем также n способами. По правилу произведения и получаем указанную формулу.
Рассмотрим задачи.
Задача 1.
Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5?
Решение. Так как порядок цифр в числе существенен, цифры могут повторяться, то это будут размещения с повторениями из пяти элементов по три (n=5, k=3), а их число равно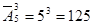 
.
Эту задачу мы могли бы решить, используя правило произведения.
Задача 2.
Сколькими способами можно раскрасить квадрат, разделенный на четыре части (на четыре равных квадрата) пятью цветами, допуская окрашивание разных частей в одинаковый цвет?
Решение. Порядок цветов имеет значение, цвета могут повторяться, следовательно, это (5,4)- размещение с повторениями. По формуле имеем:
Число всех (n,k)-размещений без повторений обозначается через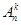 
. Подсчитаем их число.
На первое место выборки мы можем поставить любой из n элементов множества, поскольку повторения не разрешены, то на второе место мы можем поставить любой из (n-1) оставшихся элементов. На третье место - из (n-2) и так далее, вплоть до k места, куда можно поставить любой из (n-k+1) элементов. По правилу произведения имеем:
, 
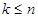
Задача 3.
Сколько различных четырехзначных чисел можно образовать из цифр 1, 2, 3,…, 9, если все цифры в каждом числе различны?
Решение. Порядок цифр существенен, цифры не повторяются, это (9,4) - размещение без повторений. Имеем:
Задача 4.
Рассмотрим задачу о квадратах в предположении, что различные части окрашиваются разными цветами. В этом случае также имеем (5,4)- размещение без повторений. По формуле имеем:
Размещения без повторений из n элементов по n называются перестановками из n элементов без повторений или перестановками множества X. Их число обозначается 
и вычисляется по формуле:
, 
.
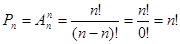Перестановки удобно представлять матрицами. Например,
Задача 5.
Рассмотрим задачу об известном квартете Крылова. Вероятно, крыловские музыканты так и не перепробовали всех возможных мест. Однако способов не так уж и много. Здесь идет перестановка из четырех элементов, значит, число перестановок равно:
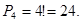
Задача 6.
Сколько различных шестизначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, если цифры в числе не повторяются?
1. Найдем количество всех перестановок из этих цифр: 
2. Цифра 0 не может стоять впереди числа, поэтому от этого числа необходимо отнять количество перестановок, при котором 0 стоит впереди. А это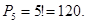 
В результате имеем:
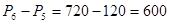различных чисел.
Разупорядочением называется перестановка n различных упорядоченных символов, при котором ни один символ не остается на своем месте. Количество разупорядочений на n различных упорядоченных символах обозначается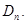 
Например, при n = 3, 
и разупорядочениями будут перестановки:
и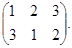 
В общем случае, для n>1 количество разупорядочений на n символах вычисляется по формуле:
Задача 7.
Семь джентльменов отправляются на вечеринку и сдают там свои шляпы. Сколькими способами непутевый гардеробщик может вернуть шляпы так, чтобы ни один из джентльменов не получил свою шляпу? Имеем разупорядочения из 7 элементов, их число равно:
.
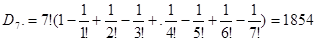Рассмотрим перестановки с повторениями.
Пусть имеются предметы r различных видов. Сколько различных комбинаций (перестановок) можно сделать из 
предметов первого вида, 
предметов второго вида,…, 
предметов вида r? Число предметов в каждой перестановке 
.
Такие комбинации называются перестановками с повторениями. Их число обозначается 
и вычисляется по формуле:
,
где n -количество всех элементов в перестановке,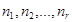 
- количество элементов каждого вида соответственно.
Задача 8.
Рассмотрим сколькими способами можно переставить буквы в слове «ананас»?
В слове шесть букв. Среди них есть одинаковые буквы:
; 
; 
.
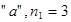Следовательно, число различных перестановок равно:
.
Задача 9.
Сколькими способами можно расположить в ряд 5 черных, 4 белых и 3 красных фишки?
Это перестановки с повторениями, имеем:
Число (n,k)-сочетанием с повторениями обозначается 
и вычисляется по формуле:
, 
Задача 10.
В кондитерском магазине продавались 4 сорта пирожных: эклеры, песочные, наполеоны и слоеные. Сколькими способами можно купить 7 пирожных.
Решение. Покупка не зависит от того, в каком порядке укладывают купленные пирожные в коробку. Сорта пирожных в покупке могут повторяться. Имеем сочетание с повторениями, n = 4, k = 7. 
.
Задача 11.
Цветочница продает розы четырех разных сортов. Сколько разных букетов можно составить из дюжины роз?
Решение. Каждый букет - это неупорядоченная выборка 12 роз с повторениями четырех возможных типов. Имеем число вариантов составления букета:
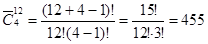
Сочетаниями без повторений из n элементов по k называются
неупорядоченные k -выборки из n элементов без повторений. Каждое (n,k)-сочетание без повторений можно упорядочить 
различными способамии получить 
различных (n,k) -размещений без повторений. Таким образом, количество вариантов при сочетании будет меньше количества размещений в раз. Ихчисло обозначается 
и вычисляется по формуле:
. 
Сочетания из n по k без повторений образуют k-элементарные подмножества исходного множества мощности n.
Задача 12.
Сколько трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр.
Решение. Так как кнопки нажимаются одновременно, то выбор этих трех кнопок – сочетание. Отсюда возможное количество комбинаций:
вариантов.
Задача 13.
У одного человека 7 книг по математике, а у второго – 9. Сколькими способами они могут обменять друг у друга две книги на две книги.
Решение. Так как порядок следования книг не имеет значения, то выбор двух книг - сочетание. Первый человек может выбрать 2 книги из 7.
способами.
Второй человек может выбрать 2 книги из 9
способами.
Значит, всего по правилу произведения возможно 
вариантов обмена книг.
Числа называются биномиальными коэффициентами, поскольку они возникают как коэффициенты при раскрытии скобок в биноме Ньютона.
, 
.
Используя эту формулу, найдем, например, разложение 
:
.
Получили всем известное соотношение. Напомним, что 
.