ПАРНОЕ ЛИНЕЙНОЕ УРАВНЕНИЕ РЕГРЕССИИ

ЛАБОРАТОРНАЯ РАБОТА №1

Цель работы: найти МНК-оценки параметров парного линейного уравнения регрессии с помощью MS Excel, а также проанализировать качество построенной модели, используя коэффициент парной корреляции, коэффициент детерминации и среднюю ошибку аппроксимации.

 

КРАТКАЯ ТЕОРИЯ

Одним из простейших уравнений регрессии, которое используется в эконометрике, является линейное уравнение:

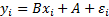(1)

где 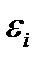– случайная величина, называемая возмущением или случайным (остаточным) членом. Слагаемое 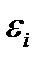вводится в уравнение регрессии для отражения того факта, что реальные значения зависимой переменной не всегда совпадают с ее условным математическим ожиданием и могут быть различными при одном и том же значении объясняющей переменной, что отражает влияние случайных, неучтенных факторов. Таким образом, не следует ожидать получения точного соотношения между какими–либо двумя экономическими показателями, за исключением тех случаев, когда оно существует по определению.

Точные значения параметров линейного уравнения регрессии (1) на практике получить невозможно. Можно только оценить 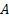, 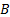и 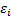, т.е. найти уравнение вида:

(2)

Здесь коэффициент 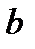называется выборочным коэффициентом регрессии 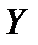по 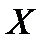. Коэффициент регрессии 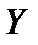по 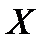показывает, на сколько единиц в среднем изменяется переменная 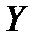при увеличении переменной 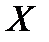на одну единицу. Коэффициент 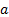называется свободным коэффициентом. Слагаемое 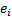в уравнении (2) называется остатком; он равен разностью в точке 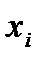между экспериментальным и расчетным значением результативного признака, т.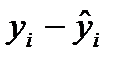е. (где ).

Для оценки параметров уравнения регрессии используется ряд методов, один из которых метод наименьших квадратов (МНК).

Оценка параметров линейного уравнения регрессии проводится по формулам:

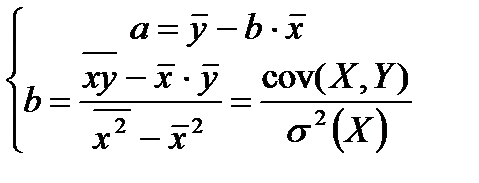(3)

 

В данной формуле – выборочный корреляционный момент или выборочная ковариация; 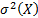– дисперсия переменной .

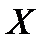Коэффициент корреляции измеряет степень и определяет направление только прямолинейных связей. Коэффициент парной корреляции 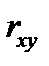есть безразмерная величина, значения которой принадлежат отрезку: 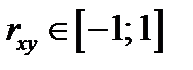. Выборочный коэффициент парной корреляции 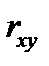вычисляется по формуле:

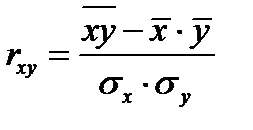, (4)

Соответствие между значениями 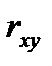и характером связи может быть представлено следующей таблицей (таблица Чеддока):

 

Значение коэффициента парной корреляции,	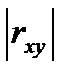Связь
	Функциональная
>0,9	Очень сильная
0,7 – 0,9	Тесная (сильная)
0,5 – 0,7	Заметная
0,3 – 0,5	Умеренная
<0,3	Слабая
	Отсутствует

Чем ближе к единице, тем теснее связь между Y и X (тем ближе связь к линейной). Геометрически это означает, что чем больше по модулю коэффициент корреляции, тем ближе экспериментальные точки прилежат к линии регрессии.

Оценку качества построенной модели (в первом приближении) дает коэффициент (индекс) детерминации и средняя ошибка аппроксимации.

Коэффициент детерминации представляет собой отношение факторной суммы квадратов к общей сумме квадратов:

, (5)

Значения 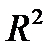лежат в промежутке [0;1]. Чем ближе значение R² к единице, тем лучше модель описывает экспериментальные данные, тем ближе точки прилежат к линии регрессии.

Коэффициент детерминации показывает, какая доля изменения (дисперсии) зависимой переменной обусловлена изменением объясняющей переменной. Например, R ²=0,75 – это значит, что на 75% изменение зависимой величины Y обусловлено изменением фактора X и на 25% – действием других неучтенных факторов.

Коэффициент детерминации равен квадрату коэффициента корреляции:

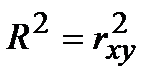
Средняя ошибка аппроксимации:

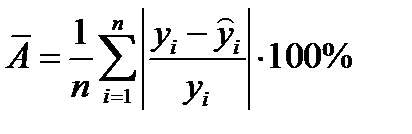, (6)

Допустимый предел значений 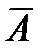, при котором качество модели считается приемлемым, – не более 8-10%.

Статистический выброс – это результат измерения, выделяющийся из общей выборки. Иными словами, выбросы – это необычно низкие или высокие значения наблюдаемой величины.

Главная опасность, которую представляют выбросы – искажение статистик или результатов статистических расчетов.

Наличие выбросов может означать ошибку ввода данных, недостаточную величину выборки или присутствие специальной причины отклонения – действие конкретного фактора или причины.

Существуют различные методы обнаружения статистических выбросов, например, метод стандартизации остатков. Это один из самых простых способов. Он основан на правиле трех сигм: вероятность выхода величины за пределы ±3σ составляет 0,0027, а значит, с большой долей вероятности, значение, которое выходит за пределы ±3σ не принадлежит к популяции.

Если верно предположение, что остатки подчиняются нормальному закону N (0, 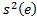), то преобразованные остатки:

должны подчиняться стандартному нормальному закону N (0,1). Тогда подозрительным на выброс являются значения отклика, для которых величины и очевидными выбросами при . В формуле (7) – исправленное среднее квадратическое отклонение остатков.

Что делать, если обнаружен выброс? Автоматическое исключение выбросов – это далеко не всегда наиболее целесообразная процедура. Выброс – экспериментальная точка, которая не типична по отношению к остальным данным. Каждое такое наблюдение должно подвергаться тщательному исследованию с целью выяснения причин его возникновения.

Выбросы должны исключаться (по согласованию с экспериментатором), если они вызваны такими причинами, как ошибки, проведение эксперимента в других условиях и т.д. Во многих случаях выбросы могут побуждать к изменению вида модели.

Удалять статистические выбросы из ряда значений нужно по одному, каждый раз перестраивая регрессию. Нельзя удалять более 1/8 части всех имеющихся наблюдений.

 

ПОСТАНОВКА ЗАДАЧИ

Для анализа зависимости объема потребления Y (тыс. руб.) домохозяйства в зависимости от располагаемого дохода X (тыс. руб.) отобрана выборка объема n = 13, результаты которой приведены в таблице:

 

 

№
	10,7	10,9	11,0	11,3	12,0	12,1	12,4	12,5	12,7	12,9	14,0	14,1	14,3
	10,2	10,5	10,8	11,0	11,5	11,8	11,9	18,1	12,4	13,0	13,1	13,4	14,0

 

Необходимо:

1. Построить корреляционное поле. Сделать предположение о характере зависимости между анализируемыми переменными.

2. Найти МНК-оценки параметров a и b парного линейного уравнения регрессии ;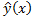

3. Проанализировать статистические данные на наличие выбросов с помощью стандартизованных остатков. Если будет обнаружен выброс, то его нужно удалить из выборки и снова найти МНК-оценки параметров линейного уравнения регрессии.

3. Найти коэффициент детерминации;

4. Рассчитать коэффициент парной корреляции и оценить степень тесноты и направление линейной связи, используя таблицу Чеддока;

5. Найти среднюю ошибку аппроксимации;

6. Построить график линейного уравнения регрессии.

 

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Расчеты в данной работе проводятся в пакете MS Excel 2007 с использованием инструмента А нализ данных.

1. Откройте MS Excel 2007.

2. Введите данные в виде столбцов, т.е. сверху вниз.

3. С помощью мастера диаграмм постройте корреляционное поле и сделайте предположение о характере распределения.

Активизируйте Мастер диаграмм. В главном меню (ленте) выберите Вставка, Точечная диаграмма:

 

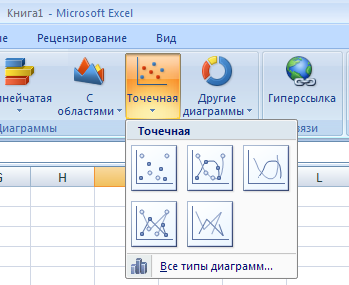
Появится поле будущего графика. Затем перейдите на вкладку Конструктор, нажмите Выбрать Данные:

 

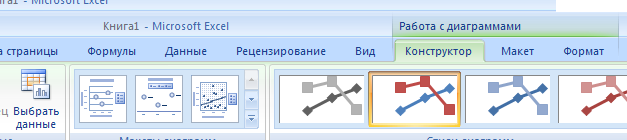
Появится новое диалоговое окно. Нажмите . Введите данные переменных X и Y. Нажмите .

Появится график. Данный график нужно преобразовать: убрать легенду, линию сетки, подписать оси. Необходимо изменить начало координат, чтобы корреляционное поле максимально заполняло поле графика.

4. Перейдите на вкладку Данные главного меню (ленты), затем Анализ данных – Регрессия. (Если на вкладке Данные нет Анализа данных, необходимо выполнить следующие действия: щелкнуть кнопку Office , затем параметры Excel, Надстройки, нажать и установить флажок на Пакет анализа.).

5. Заполните диалоговое окно инструмента Пакета анализа Регрессия.

 

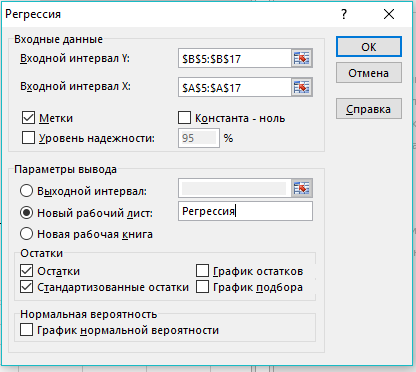
Входные данные

Входной интервал 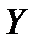– диапазон (столбец), содержащий данные результативного признака.

Входной интервал 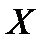– диапазон (столбец), содержащий данные факторного признака.

Метки (да или нет) – флажок, который указывает, содержит ли первая строка названия столбцов или нет. Ставим флажок в поле Остатки и Стандартизованные остатки.

В результате выбора ОК получим Итоги регрессионного анализа, содержащие 4 таблицы: Регрессионная статистика, Дисперсионный анализ, Таблица без названия, Вывод остатков.

В этой задаче вам понадобятся данные трех таблиц: