6. Проанализируйте стандартные остатки на предмет наличия статистических выбросов. Если 
, то данное измерение необходимо удалить из выборки. Затем снова выведите регрессионные итоги (т.е. повторно выполните п. 4, 5).
После удаления выбросов стандартные таблицы должны быть следующего вида:
Таблица 1
| Регрессионная статистика | |
| Множественный R | 0,980514181 |
| R-квадрат | 0,961408059 |
| Нормированный R-квадрат | 0,957548865 |
| Стандартная ошибка | 0,252699026 |
| Наблюдения |
Таблица 2.
| Коэффициенты | Стандартная ошибка | t- статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 0,323532689 | 0,741271847 | 0,436456195 | 0,671778532 | -1,328123 | 1,97518 |
| Переменная X 1 | 0,941493314 | 0,059650168 | 15,78358196 | 2,14135E-08 | 0,808584 | 1,07440 |
Таблица 3.
| Наблюдение | Предсказанное Y | Остатки | Стандартные остатки |
| 10,39751114 | -0,197511144 | -0,819755575 | |
| 10,58580981 | -0,085809807 | -0,356147335 | |
| 10,67995914 | 0,120040862 | 0,498220827 | |
| 10,96240713 | 0,037592868 | 0,156026451 | |
| 11,62145245 | -0,121452452 | -0,504079528 | |
| 11,71560178 | 0,084398217 | 0,350288634 | |
| 11,99804978 | -0,098049777 | -0,406948437 | |
| 12,28049777 | 0,119502229 | 0,495985271 | |
| 12,46879643 | 0,531203566 | 2,204721595 | |
| 13,50443908 | -0,404439079 | -1,67859485 | |
| 13,59858841 | -0,19858841 | -0,824226688 | |
| 13,78688707 | 0,213112927 | 0,884509636 |
7. Найдите параметры a и b парного линейного уравнения регрессии из второго столбца таблицы 2.
8. Запишите в бланк отчета уравнение регрессии.
9. Сделайте вывод, используя экономический смысл выборочного коэффициента регрессии 
.
Коэффициент детерминации
10. Найдите коэффициент детерминации R 2 из таблицы 1. Значение занесите в бланк отчета.
11. Сделайте вывод.
Коэффициент парной корреляции
12. Перейдите обратно в тот лист, где размещены исходные данные.
В главном меню выберите последовательно пункты: Данные – Анализ данных – Корреляция. Появится диалоговое окно:
14. Заполните диалоговое окно в соответствии с рисунком. В поле Входной интервал введите данные столбцов X и Y. Нажмите ОК. Появится новый лист, содержащий таблицу:
Таблица 4.
| Столбец 1 | Столбец 2 | |
| Столбец 1 | ||
| Столбец 2 | 0,9805 |
15. Из таблицы найдите выборочный коэффициент корреляции между переменными X и Y. Запишите значение выборочного коэффициента в бланк отчета. Сделайте вывод о силе и направлении линейной связи.
Средняя ошибка аппроксимации.
Средняя ошибка аппроксимации рассчитывается по формуле (6). Для нахождения средней ошибки аппроксимации воспользуемся таблицей 3 (Вывод остатков), расположенной в листе «Регрессия».
16. Скопируйте из таблицы 3 столбец «остатки» 
. Вставьте их рядом с исходными данными.
17. Дополните таблицу данных столбцом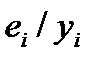 
(т.е. необходимо разделить остатки на соответствующие экспериментальные значения результативного признака).
18. Рассчитайте столбец 
. Сначала выделите ячейку, в которой хотите разместить ответ. Затем в главном меню нажмите кнопку Функция 
. В окне Категория выберите Математические, затем в окне Функция – АBS. Выделите число, для которого необходимо рассчитать абсолютное значение. Щелкните по кнопке ОК.
19. Используя процедуру Автосумма, вычислите среднее значение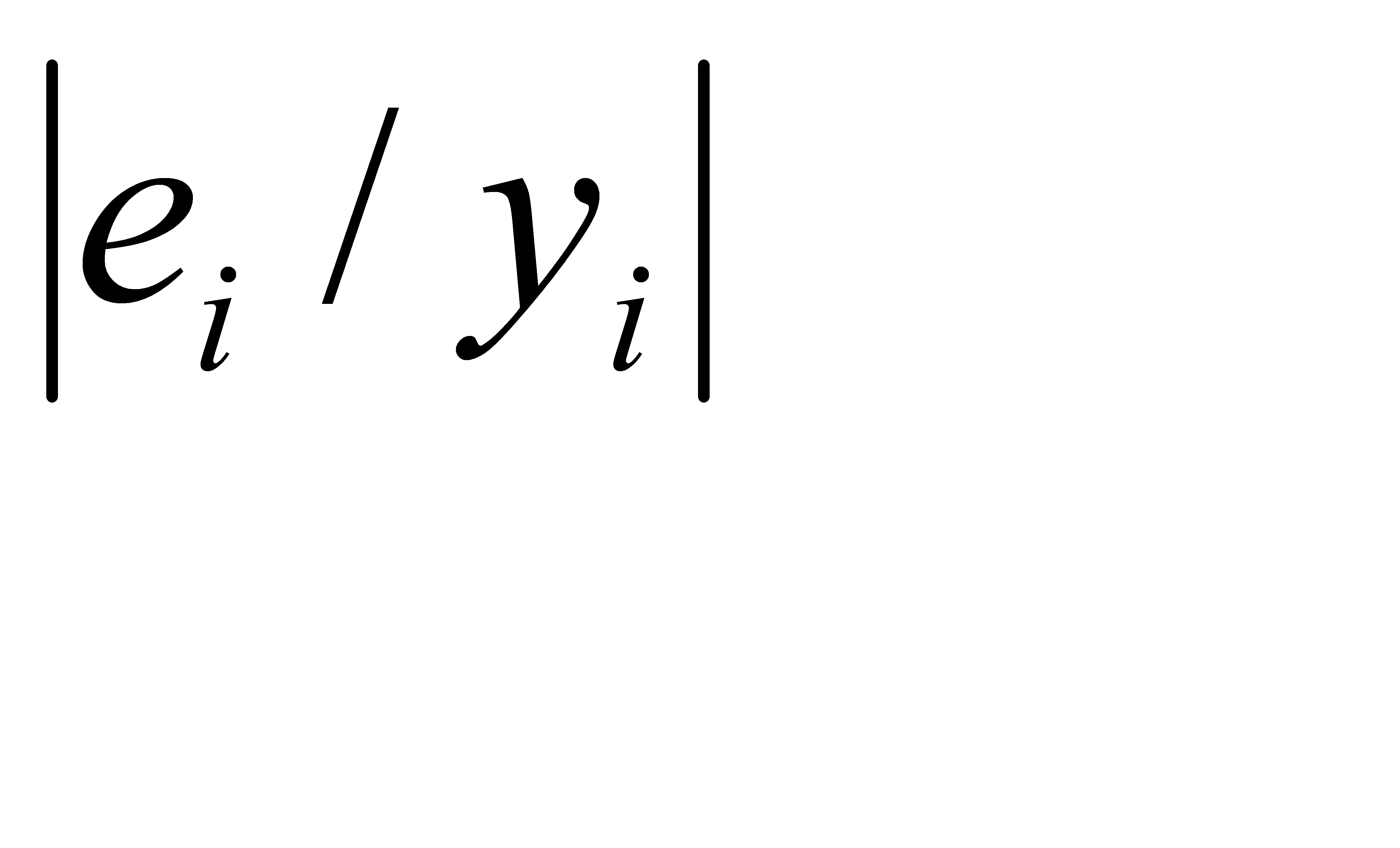 
. Умножив данное значение на 100%, получите среднюю ошибку аппроксимации.
В результате расчетов таблица примет следующий вид:
| xi, руб. | yi, руб. | ei | ei / yi | | ei / yi | |
| 10,7 | 10,2 | -0,19751 | -0,01936 | 0,019364 |
| 10,9 | 10,5 | -0,08581 | -0,00817 | 0,008172 |
| 10,8 | 0,120041 | 0,011115 | 0,011115 | |
| 11,3 | 0,037593 | 0,003418 | 0,003418 | |
| 11,5 | -0,12145 | -0,01056 | 0,010561 | |
| 12,1 | 11,8 | 0,084398 | 0,007152 | 0,007152 |
| 12,4 | 11,9 | -0,09805 | -0,00824 | 0,008239 |
| 12,7 | 12,4 | 0,119502 | 0,009637 | 0,009637 |
| 12,9 | 0,531204 | 0,040862 | 0,040862 | |
| 13,1 | -0,40444 | -0,03087 | 0,030873 | |
| 14,1 | 13,4 | -0,19859 | -0,01482 | 0,01482 |
| 14,3 | 0,213113 | 0,015222 | 0,015222 | |
| Средняя ошибка аппроксимации | 0,014953 |
20. Сделайте вывод о качестве модели.