Представление гармонических колебаний в виде проекций вращающихся векторов

Мгновенные значения функции u = U_mcos (ω t+ y) можно получить как проекцию на горизонтальную ось отрезка длиной U_m, вращающегося относительно начала прямоугольной системы координат с угловой скоростью ω = 2p f в положительном направлении (т.е. против хода часовой стрелки). Вращающийся отрезок условимся называть вектором. Этот вектор, вращающийся в плоскости прямоугольной системы координат, не следует смешивать с вектором в трехмерном пространстве из области механики или теории электромагнитного поля.

В момент t = 0 вектор образует с горизонтальной осью угол ψ и его проекция на горизонтальную ось равна U_mcos y, т.е. мгновенному значению заданной функции при t = 0 (рисунок 2.4, а).

За время t = t ₁вектор повернется на угол ω t ₁и окажется повернутым относительно горизонтальной оси на угол ω t ₁+y; его проекция на эту ось будет равна U_mcos (ω t ₁ + y) и т.д.

Таким образом, рассмотрение гармонических колебаний можно заменить рассмотрением вращающихся векторов.

Для получения мгновенных значений в соответствии с вышесказанным условимся проектировать векторы на горизонтальную ось. Рассмотрим теперь функцию U_msin (ω t + y) = U_mcos (ω t + y - ).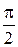

Она представится проекцией вращающегося вектора, имеющего начальную фазу y - 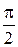(рисунок 2.4, б).

Следовательно, векторы, изображающие косинусоидальную и синусоидальную функции, взаимно перпендикулярны.

Если гармонические колебания имеют одну и ту же частоту, то соответствующие этим колебаниям векторы вращаются с одинаковой угловой скоростью и поэтому углы между ними сохраняются неизменными.

На рисунке 2.5 показаны две гармонические функции

u ₁ = U _{1 m}cos (ω t + y₁)

и

u ₂ = U _{2 m}cos (ω t + y₂),

имеющие одинаковую угловую частоту ω и начальные фазы y₁и -y₂. Кривая u ₁, смещенная влево относительно u ₂, возрастает от нуля до своего положительного максимума раньше, чем кривая u ₂. Поэтому говорят, что u ₁опережает по фазе u ₂, или, что то же, u ₂отстает по фазе от u ₁. Разность начальных фаз j = y₁ - (-y₂) = y₁ + y₂называется фазовым сдвигом или углом сдвига u ₁относительно u ₂. Этот угол и образуют между собой векторы, показанные на рисунке 2.5 (вверху).

При равенстве начальных фаз, т.е. при фазовом сдвиге, равном нулю, векторы, направлены, в одну и ту же сторону (совпадают по фазе).

При фазовом сдвиге 180° векторы направлены в диаметрально противоположные стороны (находятся в противофазе).

Диаграмма, изображающая совокупность векторов, построенных с соблюдением их взаимной ориентации по фазе, называется векторной диаграммой.

Векторное представление гармонических функций, частота которых одинакова, облегчает операции сложения и вычитания этих функций. Ввиду того, что сумма проекций двух векторов равна проекции геометрической суммы этих векторов, амплитуда и начальная фаза результирующей кривой легко находятся из векторной диаграммы геометрическим сложениемвекторов.

Например, пусть требуется сложить функции

u ₁ = U _{1 m}cos (ω t + y₁)и u ₂ = U _{2 m}cos (ω t + y₂).

Из графического построения рисунок 2.6, а следует:

; (2.11)

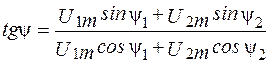. (2.12)

Здесь угол y находится с учетом знаков числителя и знаменателя, определяющих знаки синуса и косинуса.

В случае, когда функция u ₂вычитается из u ₁(рисунок 2.6, б), угол y₁в (2.11) и (2.12) заменяется на y₂ + p или, что то же, на y₂-(-p).

Амплитуда U_m и угол y могут быть также получены непосредственно из векторной диаграммы.

При пользовании векторной диаграммой с целью установления фазовых сдвигов или амплитудных значений гармонических величин, имеющих одинаковую частоту, векторная диаграмма может считаться неподвижной (при равенстве частот углы между векторами не зависят от времени).

Построение векторных диаграмм обычно не связано с определением мгновенных значений гармонических функций; в таких случаях векторные диаграммы строятся не для амплитуд, а для действующих значений, т.е. модули векторов уменьшаются по сравнению с амплитудами в 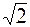раз. При этом векторная диаграмма мыслится неподвижной.