СОПРЯЖЕНИЕ ДВУХ ОКРУЖНОСТЕЙ

Возможны два варианта построений сопряжений двух окружностей:

· Задан радиус сопряжения.

· Задана точка сопряжения на одной из окружностей.

Сопряжение может быть внешним, внутренним и смешанным.

1. Сопряжение двух окружностей дугой заданного радиуса R (Рисунок16)

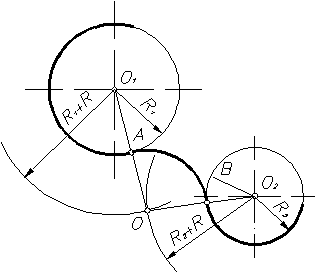
Рисунок 16

При внешнем сопряжении (рисунок 16) центр сопряжения О определяется пересечением двух геометрических мест – вспомогательных окружностей радиусов R₁ + R и R₂ + R, проведенных соответственно из центров сопрягаемых дуг, то есть из точек О₁ и О₂. Точки сопряжения А и В определяются как точки пересечения заданных дуг с прямыми ОО₁ и ОО₂.

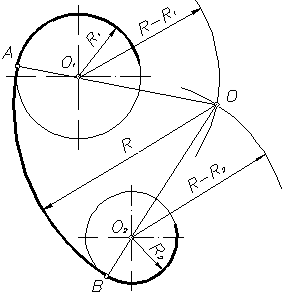
Рисунок 17

При внутреннем сопряжении (рисунок 17) центр сопряжения О определяется пересечением двух геометрических мест – вспомогательных окружностей радиусов R – R₁ и R – R₂, проведенных соответственно из О₁ и О₂ (рисунок 17).

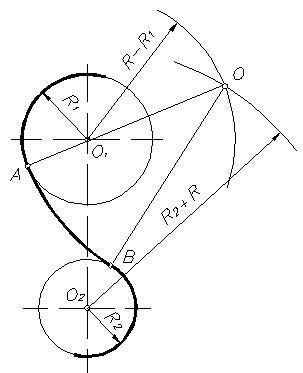
Рисунок 18

При смешанном сопряжении (рисунок 18) центр сопряжения О определяется в пересечении вспомогательных окружностей радиусов R - R₁ и R + R₂, проведенных соответственно из О₁ и О₂. Точки сопряжения А и В лежат на пересечении линий центров ОО₁ и ОО₂ с дугами заданных окружностей.

2. Сопряжение двух окружностей, если задано точка сопряжения А на одной из окружностей (рисунок 19).

Соединяют точку А с центром О₁ и откладывают на этой прямой отрезок АС, равный R₂. К середине отрезка СО₂ восставляют перпендикуляр до пересечения с продолжением линии О₁А. Точка О пересечения и является центром сопряжения. Вторая точка сопряжения В лежит на пересечении линии центров ОО₂ с дугой второй окружности.

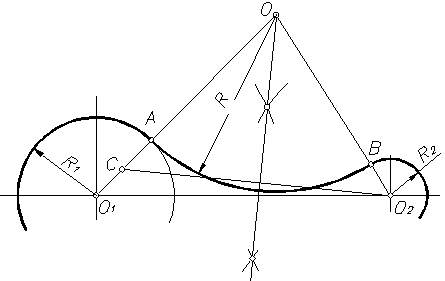
Рисунок 19

ПОСТРОЕНИЕ КАСАТЕЛЬНЫХ

Построение касательных к окружности основано на том, что касательная перпендикулярна к радиусу, проведенному в точку касания.

1. Касательная к окружности из точки А, лежащей вне окружности (рисунок 20).

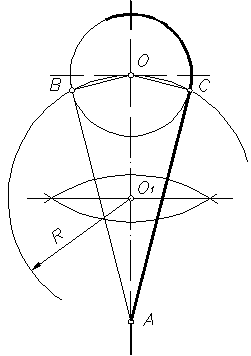
Рисунок 20

Отрезок ОА, соединяющий данную точку с центром окружности, делят пополам и из полученной О₁, как из центра описывают вспомогательную окружность радиусом R = О₁А. Вспомогательная окружность пересекает заданную в точке С. Прямая АС является касательной к окружности, так как угол АСО прямой, как вписанный в окружность и опирающийся на ее диаметр.

2. Касательная к двум окружностям может быть внешней, если обе окружности расположены с одной стороны от нее, и внутренней, если окружности расположены с разных сторон от касательных.

2.1 Внешняя касательная к окружностям радиусов R₁ и R₂ (рисунок 21).

Рисунок 21

Из центра О₁ большей окружности проводят вспомогательную окружность радиусом R₁ – R₂. Отрезок О₁О₂ делят пополам и проводят вспомогательную окружность радиусом R = О₃О₁. Точки пересечения этих окружностей соединяют с центром О₁ и продолжают до пересечения с окружностью радиуса R₁ в точках В и D. Эти точки являются точками касания окружности большего диаметра. Из центра О₂ проводят прямые О₂А и О₂С, соответственно параллельные О₁В и ОD, до пересечения с контуром окружности в точках А и С. Прямые АВ и СD – искомые внешние касательные к двум окружностям.

2.2 Внутренняя касательная к двум окружностям радиусов R₁ и R₂ (рисунок 22).

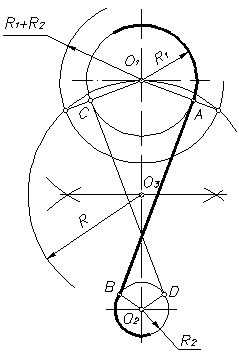
Рисунок 22

Из центра окружности О₁ проводят вспомогательную окружность радиусом R₁ + R₂. Делят отрезок О₁О₂ пополам, и из полученной точки О₃ проводят вторую вспомогательную окружность радиусом R = О₃О₁. Точки пересечения этих окружностей соединяют с центром О₁ и на пересечении с окружностью радиуса R₁ получают точки касания А и С. Из точки О₂ проводят прямую, параллельную прямой О₁А, и получают точку касания В на малой окружности. Аналогично построена точка касания D. Прямые АВ и СD – искомые внутренние касательные к двум окружностям.