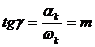- время запаздывания в объекте;
- время запаздывания в объекте;
 - коэффициент передачи астатического объекта регулирования.
- коэффициент передачи астатического объекта регулирования.
12.1.3. Графо - аналитический расчет настроек АСР по запасу устойчивости, по модулю и фазе.
12.1.3.1. АСР с П и И - регуляторами
Если АФХ объекта имеет вид, показанный на рисунке 12.8. а,б, а необходимый запас устойчивости по модулю С и фазе g, то можно записать следующее соотношение для П - регулятора (рис. 12.8 а).



 jV(ω) jV(ω)
jV(ω) jV(ω)
 | |||||||
 | |||||||
 |  | ||||||
 С С
С С












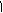




 -1 А2
-1 А2 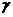 -1
-1 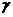

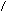



 Д4 Д1 0 u(ω) Д4 Д1 0 ω1 u(ω)
Д4 Д1 0 u(ω) Д4 Д1 0 ω1 u(ω)







 А1 900
А1 900
Д2 Д3 Д2 Д3 ω2 А1

 Wоб(jω) A2 Wоб(jω)
Wоб(jω) A2 Wоб(jω)
а) П – регулятор б) И - регулятор
Рис.12.8.


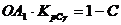
Для И - регулятора (рис. 12.8 б)

 ;
; 
где
 - коэффициент передачи регулятора, обеспечивающий запас устойчивости по модулю С;
- коэффициент передачи регулятора, обеспечивающий запас устойчивости по модулю С;
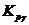 - коэффициент передачи регулятора, обеспечивающий запас устойчивости по фазе g;
- коэффициент передачи регулятора, обеспечивающий запас устойчивости по фазе g;
 - коэффициент передачи регулятора, обеспечивающий запас устойчивости по модулю С и фазе g.
- коэффициент передачи регулятора, обеспечивающий запас устойчивости по модулю С и фазе g.
Эти соотношения позволяют найти параметры настройки П и И - регуляторов
(табл. 12.3)
Таблица 12.3
| регулятор | Параметры настройки П и И - регуляторов, при которых АСР выходит на границу заданного запаса устойчивости | ||
| по модулю С | по фазе g | по модулю С и фазе g | |
| П И | 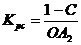

| 

| 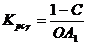

|
12.1.3.2. АСР с ПИ - регулятором
Включение ПИ - регулятора приводит к тому, что к каждому вектору  добавляется вектор
добавляется вектор  , повернутый на 90º по часовой стрелке и измененный по модулю в
, повернутый на 90º по часовой стрелке и измененный по модулю в  раз (рис. 12.9).
раз (рис. 12.9).
Из рисунка 12.9 а следует, что модуль  АФХРС является гипотенузой
АФХРС является гипотенузой  . Гипотенуза любого прямоугольного треугольника является диаметром окружности, в которую вписан этот треугольник. Это дает возможность найти интересующие нас параметры настройки Кр и Ти с помощью следующих построений.
. Гипотенуза любого прямоугольного треугольника является диаметром окружности, в которую вписан этот треугольник. Это дает возможность найти интересующие нас параметры настройки Кр и Ти с помощью следующих построений.
 |
jV(ω)


 φpc(ωk)
φpc(ωk)

 0 Aоб(ωк) u(ω)
0 Aоб(ωк) u(ω)
 kpAоб(ωк)
kpAоб(ωк)
Ak 
 Apc(ωk)
Apc(ωk)

 900
900 

 Bk
Bk

 Дк
Дк 
Рис.12.9.
1. Запас устойчивости по модулю С (рис. 12.10).
Из рисунка 12.10 следует:

 jV(ω)
jV(ω)
 |
 С
С








 -1 0
-1 0

 Д4 Д1 u(ω)
Д4 Д1 u(ω)
Bk Аk
Wоб(jω)
Рис.12.10.
Отсюда
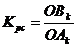 ;
; 
2. Запас устойчивости по фазе (рис. 12.11)
 jV(ω)
jV(ω)
 |

 -1
-1 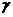





 Д4 0 u(ω)
Д4 0 u(ω)




 Д2 Ak
Д2 Ak
Ck Wоб(jω)
Рис.12.11.
В соответствии с рисунком 12.11
 ,
,
 ,
,
Отсюда
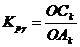 ,
, 
3. Запас устойчивости по модулю С и фазе g (рис. 12.12)
 jV(ω)
jV(ω)
 |
С




 -1
-1






 Д4 Д1 0 u(ω)
Д4 Д1 0 u(ω)

 Ak
Ak
 Д2 Д3
Д2 Д3
Ek Wоб(jω)
Рис.12.12.
Из рисунка 12.12 имеем
 ,
,

Следовательно
 ;
; 
Расчетные соотношения сведены в таблицу 12.4.
Таблица 12.4
| Параметры настройки ПИ – регулятора, при которых АСР выходит на границу заданного запаса устойчивости | ||
| по модулю С | по фазе g | по модулю С и фазе g |


| 

| 

|
4. Далее по данным табл. 12.4 чертятся кривые границ заданного запаса устойчивости в плоскости параметров Кр-Ти, проводятся касательные к ним из начала координат и находятся оптимальные значения настроечных параметров Кропт и Тиопт (рис.12.13).
 Кр
Кр



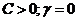



 Крс
Крс 

 Кр
Кр 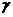





 Крс
Крс 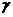
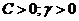
 0 Ти
0 Ти
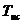

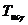
Рис.12.13.
12.1.3.3. АСР с ПИД - регулятором
Включение ПИД - регулятора приводит к добавлению к векторам  векторов
векторов  , повернутых на 90º по часовой стрелке и измененных по модулю в
, повернутых на 90º по часовой стрелке и измененных по модулю в  раз (рис. 12.14).
раз (рис. 12.14).
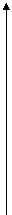 |
jV(ω)


 φpc(ωk)
φpc(ωk)

 0 Aоб(ωк) u(ω)
0 Aоб(ωк) u(ω)
 kpAоб(ωк)
kpAоб(ωк)
Ak 
 Apc(ωk)
Apc(ωk)

 900
900 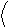
 Bk
Bk

 Дк
Дк 
Рис.12.14.
Это позволяет находить настроечные параметры ПИД - регулятора с помощью графических построений (табл. 12.5), аналогичных случаю АСР с ПИ - регулятором.
Таблица 12.5
| Параметры настройки ПИД - регулятора, при которых АСР выход на границу заданного запаса устойчивости | ||
| по модулю С | по фазе g | по модулю С и фазе g |
                                        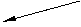   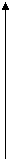  С
-1
0
Д1 Ак
Вк
Wоб(jω)
С
-1
0
Д1 Ак
Вк
Wоб(jω)
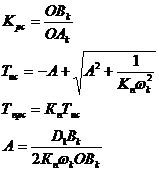
|
-1 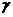 0
Ak
Д2
Ск Wоб(jω)
0
Ak
Д2
Ск Wоб(jω)
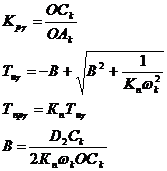
|
-1 С 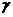 0
Ак
Д3
Ек Wоб(jω)
0
Ак
Д3
Ек Wоб(jω)

|
Построив по данным таблицы 12.5 границы заданного запаса устойчивости в плоскости параметров Кр-Ти (рис. 12.13),находят оптимальные значения настроек ПИД - регулятора.
12.1.4. Определение оптимальных настроек АСР с помощью расширенных АФХОР
12.1.4.1. Расширенная АФХ
При анализе устойчивости с помощью критерия Найквиста на к омплексную переменную передаточной функции накладывалось ограничение  .
.
Введем расширенное ограничение

где  - степень колебательной устойчивости. Этим поставлено условие, чтобы корни характеристического уравнения АСР располагались внутри контура АОВ
- степень колебательной устойчивости. Этим поставлено условие, чтобы корни характеристического уравнения АСР располагались внутри контура АОВ
(рис. 12.15) комплексной плоскости или чтобы комплексная переменная Р передаточной функции изменялась по закону

 jV(ω)
jV(ω)
 B
B

|