,
вытекающей из рисунка 13.3.
yз(t)
|
|
|
 |  | ||||||
 | |||||||
 | |||||||
|
yрст(t)
yзк(t)+y1(t)
 | |||||
 | |||||
 |
Рис.13.3.
13.3. Двухконтурная АСР с дополнительным сигналом из промежуточной точки объекта регулирования
Примером такой АСР является система регулирования температуры пара первичного перегрева (рис. 13.4).
ПП
|
|
КВ (tпп,0C)
y(t)
y1(t) (tпп,0C)
 | |||
 | |||
КпВ
Рис.13.4.
На рисунке:
КВ – коллектор впрыска;
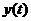- основная регулируемая величина (температура пара за пароперегревателем
ПП);
- температура пара за КВ (дополнительная регулируемая величина);
РТ – регулятор температуры пара за ПП;
Д – дифференциатор;
КлВ – клапан впрыска.
В качестве впрыскиваемой воды может применяться общестанционный конденсат, питательная вода, собственный конденсат.
Дифференциатор в системе применен не для реализации ПИД – закона регулирования, а для формирования исчезающего в статике дополнительного сигнала.
Схеме на рисунке 13.4 соответствует структурная схема, приведенная на рисунке 13.5.
f(t)
|
|
yз(t) y(t)
tппз (tпп)
- - yд(t)
Д
|
y(t) (tпп)
(tпп)
Рис.13.5.
Для такой АСР можно рекомендовать следующую последовательность расчета настроек.
1. Расчет настроек дифференциатора
Заменяя внутренний контур с обратной связью, в которой имеется дифференциатор, контуром с единичной обратной связью, рабочую структурную схему (рис. 13.5) можно представить в виде структурной схемы, приведенной на рисунке 13.6.
Эта схема принципиально не отличается от структурной схемы системы со стабилизирующим и корректирующим регуляторами. Однако, особенностью ее является то, что корректирующий регулятор в обязательном порядке должен быть
ПИ – регулятором, в котором роль коэффициента передачи играет 
, а роль времени изодрома – постоянная времени дифференциатора Тд.
{ 
; 
; 
}
Рk
|
|
|
|
yз(t) y(t)
tппз
- -
y(t) Wобэ1
y1(t)
Рис.13.6.
Далее, считая, что внутренний контур значительно менее инерционен по сравнению с внешним, рассчитывают настройку корректирующего ПИ – регулятора по передаточной функции эквивалентного объекта
По найденным настройкам корректирующего ПИ – регулятора находят значения настроечных параметров дифференциатора
; 
.
2. Расчет настроек регулятора
Исходную структурную схему (рис. 13.5) преобразуют к виду, удобному для расчета настроек регулятора (рис. 13.7).
|
|
|
y(t)+yд(t)
- -
|
Wобэ2(p)
Рис.13.7.
В соответствии с рисунком 13.7 эквивалентный объект, характеристики которого должны быть использованы для расчета настроек регулятора, описывается передаточной функцией
или
.
14. Определение параметров настройки АСР с нелинейными
Регуляторами
14.1 Введение
Наибольшее распространение в нелинейных АСР получили релейные двухпозиционные регуляторы, статическая характеристика которых изображена на рисунке 14.1, и релейные регуляторы с постоянной скоростью исполнительного механизма (ИМ).
yp 
-a +a
+B
2а 0 -B z(t)
Рис.14.1.
Для аналитического расчета такого класса нелинейных (релейных) АСР разработаны сравнительно простые методы определения значения параметров настройки.
14.2 АСР с двухпозиционным регулятором
Структурная схема АСР с двухпозиционным регулятором (ДР) представлена на рисунке 14.2
f(t)
|
|
|
 |  |  |  | ||||||||
 | |||||||||||
 |
-
Рис.14.2.
1. Если объект регулирования является идеальным интегрирующим звеном с передаточной функцией
,
то при поступлении на вход объекта регулирующего воздействия 
(рис. 14.3 а) в соответствии со статической характеристикой (рис. 14.1) регулятора регулируемая величина 
) будет изменяться по линейному закону )= 
. Если на вход объекта от регулятора будет подано воздействие 
, то регулируемая величина будет изменяться по линейному закону )= 
, т.е. в обратную сторону.
При этом в замкнутой АСР при релейной статической характеристике регулятора с зоной
yp(t)
+B
t1 t2
 | |||||
 | |||||
 | |||||
 |
0 Tk t
 |
-B
а)
+a
0 t
-a 
t1 t2
Tk
б)
Рис.14.3.
неоднозначности 2а (рис. 14.1) в установившемся режиме возникнут устойчивые автоколебания (рис. 14.3 б).
2. Если объект является апериодическим звеном первого порядка с передаточной функцией
,
то при поступлении на его вход регулирующего воздействия 
(рис. 14.4 а) регулируемая величина
yp(t)
+B
t1 t2
t
0 Tk
|
-B
y(t) а)
+KобB
+a