Если D - односвязная ограниченная область, w = f (z) - аналитическая в этой области функция, то для любого кусочно-гладкого замкнутого контура L, лежащего в D, интеграл от f (z) по L равен нулю:  .
.
Доказательство. Удивительно, но эта важнейшая теорема непосредственно и просто следует из условий Коши-Римана и формулы Грина. Так как, по доказанному выше, 
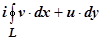 , то, применяя к действительным криволинейным интегралам формулу Грина, получим
, то, применяя к действительным криволинейным интегралам формулу Грина, получим  вследствие условий Коши-Римана
вследствие условий Коши-Римана  . Символом G в доказательстве обозначена область, заключённая внутри контура L.
. Символом G в доказательстве обозначена область, заключённая внутри контура L.
 Следствие. Для всех кусочно-гладких кривых, лежащих внутри области D, в которой аналитична функция w = f (z), и имеющих общие начальную и конечную точки, интеграл
Следствие. Для всех кусочно-гладких кривых, лежащих внутри области D, в которой аналитична функция w = f (z), и имеющих общие начальную и конечную точки, интеграл  имеет одинаковое значение.
имеет одинаковое значение.
Доказательство: Объединение  кривых - замкнутый контур, поэтому
кривых - замкнутый контур, поэтому  .
.
 7. Теорема Коши для многосвязной области. Если функция w = f (z) аналитична в замкнутой многосвязной ограниченной области
7. Теорема Коши для многосвязной области. Если функция w = f (z) аналитична в замкнутой многосвязной ограниченной области 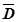 , ограниченной контурами L 0 (внешняя граница), L 1, L 2, …, Lk, то интеграл от f (z), взятый по полной границе области
, ограниченной контурами L 0 (внешняя граница), L 1, L 2, …, Lk, то интеграл от f (z), взятый по полной границе области 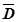 , проходимой так, что область остаётся с одной стороны, равен нулю.
, проходимой так, что область остаётся с одной стороны, равен нулю.
Доказательство Рассмотрим случай, когда граница области 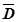 (на рисунке область заштрихована) состоит из внешнего контура L 0 и внутренних контуров L 1 и L 2. Соединим контур L 0разрезом FM с контуром L 1, разрезом BG - с контуром L 2. Область
(на рисунке область заштрихована) состоит из внешнего контура L 0 и внутренних контуров L 1 и L 2. Соединим контур L 0разрезом FM с контуром L 1, разрезом BG - с контуром L 2. Область  с границей
с границей  односвязна, поэтому для неё справедлива интегральная теорема Коши:
односвязна, поэтому для неё справедлива интегральная теорема Коши:
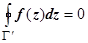 . Интегралы по каждому из разрезов входят в этот общий интеграл дважды в противоположных направлениях и, как следствие, взаимно уничтожаются, поэтому остаются только интегралы по контурам, проходимым так, что область остаётся с одной стороны.
. Интегралы по каждому из разрезов входят в этот общий интеграл дважды в противоположных направлениях и, как следствие, взаимно уничтожаются, поэтому остаются только интегралы по контурам, проходимым так, что область остаётся с одной стороны.
Буквами без верхнего индекса будем обозначать контуры, проходимые против часовой стрелки, с верхним минусом - по часовой. Мы доказали, что  . Таким образом, интеграл по внешнему контуру равен сумме интегралов по внутренним контурам, при этом все контуры обходятся в одном направлении.
. Таким образом, интеграл по внешнему контуру равен сумме интегралов по внутренним контурам, при этом все контуры обходятся в одном направлении.
8. Интегральная формула Коши. Пусть w = f (z) аналитична в области D и L - замкнутая кусочно-гладкая кривая, содержащаяся в D вместе с областью D 1, которую она ограничивает. Тогда для каждой точки  имеет место формула
имеет место формула
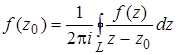 .
.
Доказательство. Заметим, что в этой формуле функция в точке z 0 портится как раз введением множителя  . Окружим точку z 0 окружностью
. Окружим точку z 0 окружностью  радиуса
радиуса  столь малого, что на
столь малого, что на  f (z) мало отличается от f (z 0):
f (z) мало отличается от f (z 0):  , тогда
, тогда  . Более строго, возьмём
. Более строго, возьмём  столь малым, что окружность
столь малым, что окружность  радиуса
радиуса  с центром в f (z) лежит в D 1. Функция w = f (z) аналитична в двусвязной области, заключенной между L и
с центром в f (z) лежит в D 1. Функция w = f (z) аналитична в двусвязной области, заключенной между L и  , поэтому (следствие из Теоремы Коши для многосвязной области)
, поэтому (следствие из Теоремы Коши для многосвязной области)  . Распишем последний интеграл:
. Распишем последний интеграл: 
 . Второй интеграл здесь равен
. Второй интеграл здесь равен  . Первый интеграл а) не зависит от
. Первый интеграл а) не зависит от  (действительно, подынтегральная функция аналитична в области между
(действительно, подынтегральная функция аналитична в области между  и
и  , где
, где  - окружность радиуса
- окружность радиуса  , и по тому же следствию из Теоремы Коши для многосвязной области
, и по тому же следствию из Теоремы Коши для многосвязной области  ; б)
; б)  . Из этих утверждений а) и б) следует, что первый интеграл
. Из этих утверждений а) и б) следует, что первый интеграл  .
.
Докажем утверждение б). Обозначим  , при этом, вследствие непрерывности функции,
, при этом, вследствие непрерывности функции,  . Оценим
. Оценим  по модулю (учитывая, что
по модулю (учитывая, что  ):
): 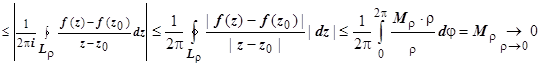 . Утверждение доказано. Доказана и интегральная формула Коши:
. Утверждение доказано. Доказана и интегральная формула Коши: 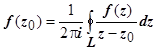 .
.
9. Бесконечная дифференцируемость аналитической функции. Запишем интегральную формулу Коши в переменных z, t:  . Продифференцируем эту формулу по z:
. Продифференцируем эту формулу по z:  . Продолжим дифференцирование:
. Продолжим дифференцирование:  ;
; 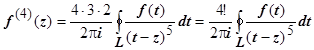 , и вообще
, и вообще  . Следовательно:
. Следовательно:
Если функция f (z) имеет в каждой точке области D производную первого порядка (т.е. аналитична в области D), то она имеет в этой области производную любого порядка (т.е. любая производная функции f (z) аналитична в области D).
10. Ряд Тейлора. Пусть функция w = f (z) аналитична в области D,  . Обозначим L окружность с центром в z 0, принадлежащую области D вместе с ограниченным ею кругом. Тогда для любой точки z, лежащей внутри L,
. Обозначим L окружность с центром в z 0, принадлежащую области D вместе с ограниченным ею кругом. Тогда для любой точки z, лежащей внутри L,  . Представим множитель
. Представим множитель  в виде суммы сходящейся геометрической прогрессии:
в виде суммы сходящейся геометрической прогрессии:  (так как
(так как
| z – z 0| < | t – z 0|, то  )
)  , и ряд сходится абсолютно, поэтому его можно почленно интегрировать:
, и ряд сходится абсолютно, поэтому его можно почленно интегрировать: 
 , так как
, так как  . Итак,
. Итак,
 .
.
Ряд в правой части этого равенства - ряд Тейлора функции f (z). Этот ряд абсолютно сходится внутри контура L, а в качестве L можно взять любую окружность, которая не выходит за пределы области D.
11. Ряд Лорана. Пусть функция f (z) аналитична в кольце  . Тогда для любой точки этого кольца
. Тогда для любой точки этого кольца  ; при этом окружности проходятся так, что область остаётся слева. Изменим в интеграле по внутренней окружности направление обхода на противоположное:
; при этом окружности проходятся так, что область остаётся слева. Изменим в интеграле по внутренней окружности направление обхода на противоположное:  . Интеграл по внешней окружности преобразуем так, как и при выводе формулы Тейлора:
. Интеграл по внешней окружности преобразуем так, как и при выводе формулы Тейлора:  (так как | z – z 0| < | t – z 0|, то
(так как | z – z 0| < | t – z 0|, то  )
)  , и ряд сходится абсолютно, поэтому его можно почленно интегрировать:
, и ряд сходится абсолютно, поэтому его можно почленно интегрировать:

 , где
, где  . Интеграл по внутренней окружности преобразуем аналогично, учитывая только, что на
. Интеграл по внутренней окружности преобразуем аналогично, учитывая только, что на 
| t – z 0| < | z – z 0|: 
 . И здесь ряд сходится абсолютно, поэтому его можно почленно интегрировать:
. И здесь ряд сходится абсолютно, поэтому его можно почленно интегрировать:

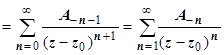 , где
, где  . Переобозначим
. Переобозначим  , тогда форма коэффициентов ряда для
, тогда форма коэффициентов ряда для  совпадёт с формой коэффициентов ряда для LR:
совпадёт с формой коэффициентов ряда для LR:  поэтому окончательно для интеграла по
поэтому окончательно для интеграла по  получим
получим  . Докажем, что и контур для вычисления коэффициентов может быть взят один и тот же. Действительно, пусть
. Докажем, что и контур для вычисления коэффициентов может быть взят один и тот же. Действительно, пусть  - кусочно-гладкий контур, расположенный в кольце
- кусочно-гладкий контур, расположенный в кольце  , и точка
, и точка 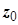 расположена внутри этого контура. По теореме Коши для многосвязной области
расположена внутри этого контура. По теореме Коши для многосвязной области 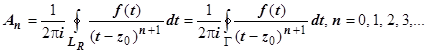 ;
;  , поэтому для любого n
, поэтому для любого n  , и
, и
 .
.
Этот ряд (содержащий и положительные, и отрицательные степени z – z 0), называется рядом Лорана функции f (z). Его часть, содержащая неотрицательные степени ( ), называется правильной; часть, содержащая отрицательные степени (
), называется правильной; часть, содержащая отрицательные степени ( ), называется главной. Правильная часть, по самому своему построению, сходится в круге | z – z 0| < R, главная - во внешности круга
), называется главной. Правильная часть, по самому своему построению, сходится в круге | z – z 0| < R, главная - во внешности круга 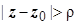 , поэтому весь ряд сходится в пересечении этих областей, т.е. в кольце
, поэтому весь ряд сходится в пересечении этих областей, т.е. в кольце  . Так же, как и для ряда Тейлора, разложение в ряд Лорана единственно
. Так же, как и для ряда Тейлора, разложение в ряд Лорана единственно