Рассмотрим необходимые шаги решения задачи оптимального планирования на примере.
Шаг 1. Выделить на листе Excel ячейки для всех параметров задачи, снабдить их содержательными пояснениями и заполнить значения внешних параметров. От того, что выбирается в качестве строк и столбцов матриц, зависит удобство написания формул. На рис. 3 представлено возможное расположение параметров (выделены цветом) и пояснений для задачи об оптимальном планировании производства.
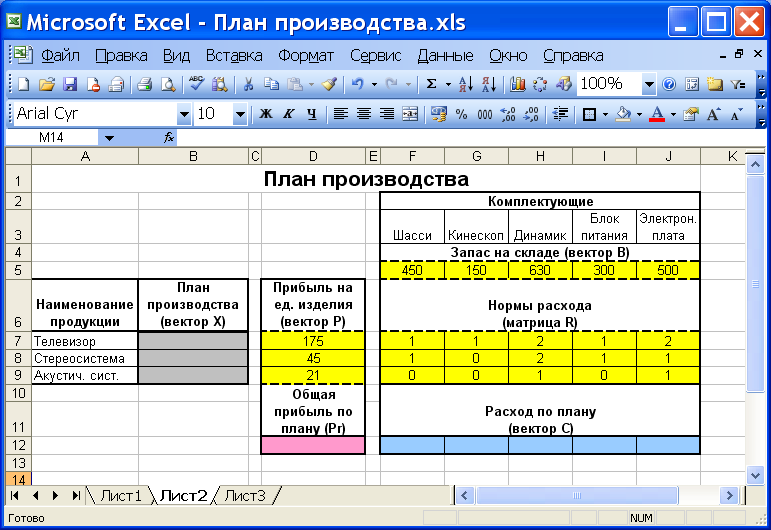
Рис. 3. Расположение параметров задачи.
Шаг 2. В ячейки независимых параметров заносятся начальные значения (например, нули), а в ячейки зависимых параметров заносятся определяющие их формулы. В нашем примере в ячейки B7:B9 (вектор плана X) заносятся нули, в ячейку D12 (прибыль Pr) – формула
=СУММПРОИЗВ(B7:B9;D7:D9),
А в ячейки F12:J12 (вектор расхода С) – матричная формула
=МУМНОЖ(ТРАНСП(B7:B9);F7:J9).
В результате вычислений все эти формулы сразу дадут нули.
Шаг 3. Вызывается программа «Поиск решения». Вызов решения осуществляется по-разному в Excel 2003, 2007 и 2010.
Excel 2003
В меню Сервис программы Excel выбирается строка Поиск решения. Если её там не оказывается, выбирается строка Надстройки … (рис. 4 слева) и в появившемся окне Надстройки устанавливается флажок Поиск решения (рис. 4 справа). После нажатия кнопки ОК будет автоматически установлена программа Solver, и её нужно вызвать из меню Сервис/Поиск решения.
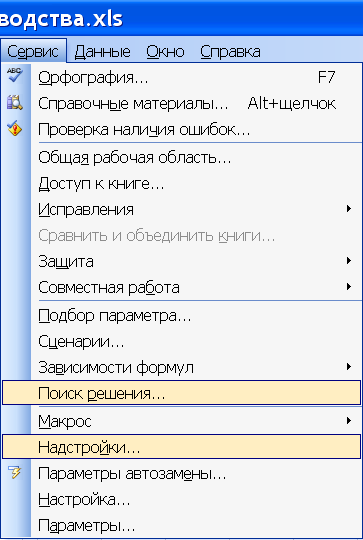

Рис. 4. Установка и вызов программы «Поиск решения» в Excel 2003.
Excel 2007/2010
Во вкладке Данные ленты инструментов программы Excel 2007/2010выбирается инструмент Поиск решения (рис. 5). Если его там не оказывается, в Excel 2007 следует нажать кнопку меню Office (рис. 6 слева), а в Excel 2010 – меню Файл (рис. 6 справа), и выбрать пункт Параметры.
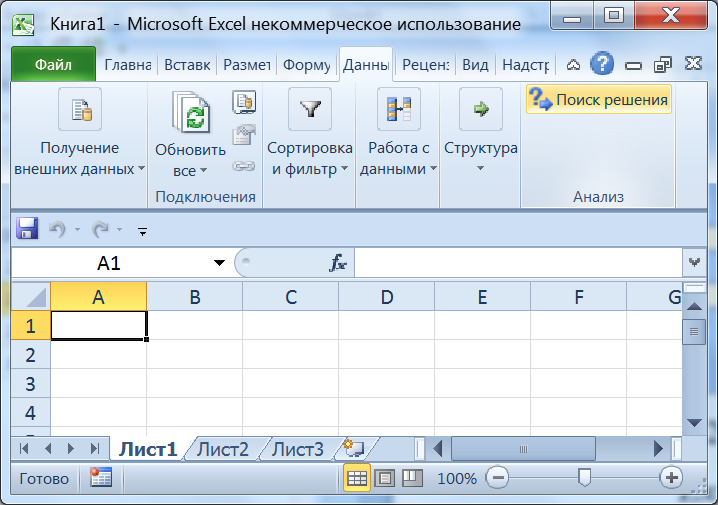
Рис. 5. Вызов программы «Поиск решения» в Excel 2007/2010.
| Кнопка Office |
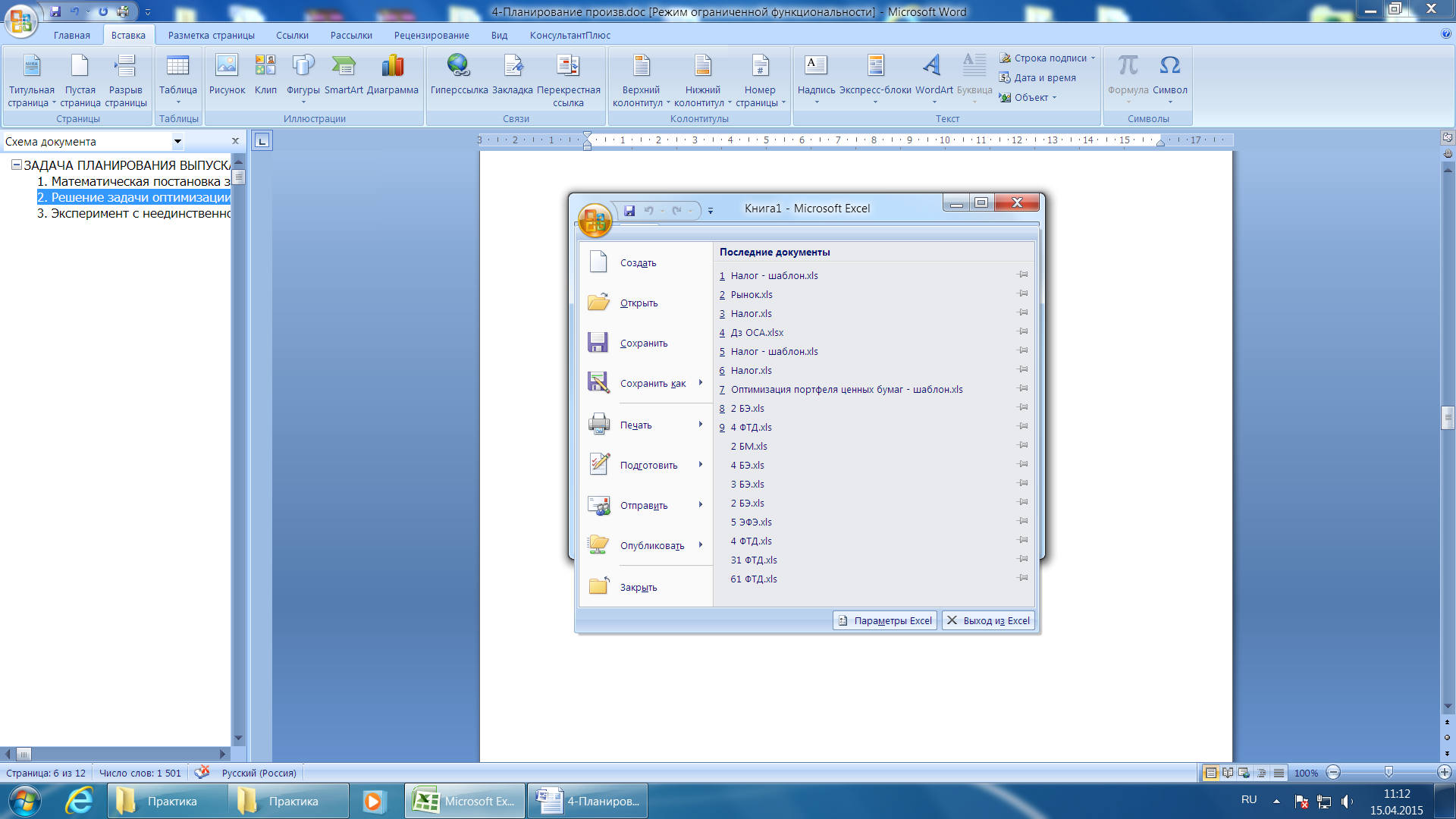
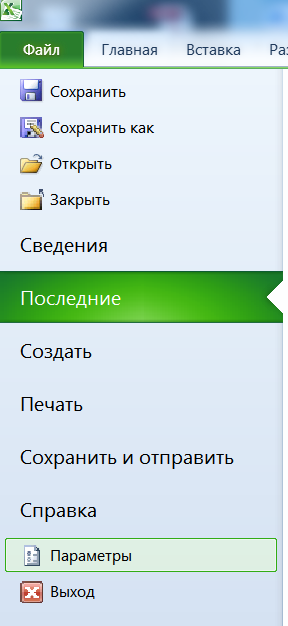
Рис. 6. Открытие параметров в Excel 2007/2010.
В появившемся окне Параметры Excel (рис. 7 слева) нужно выбрать раздел Надстройки, в нём выбрать Поиск решения и нажать кнопку Перейти. В появившемся затем окне Надстройки (рис. 7 справа) нужно установить флажок Поиск решения и нажать кнопку ОК. После этого во вкладке Данные появится нужный инструмент.
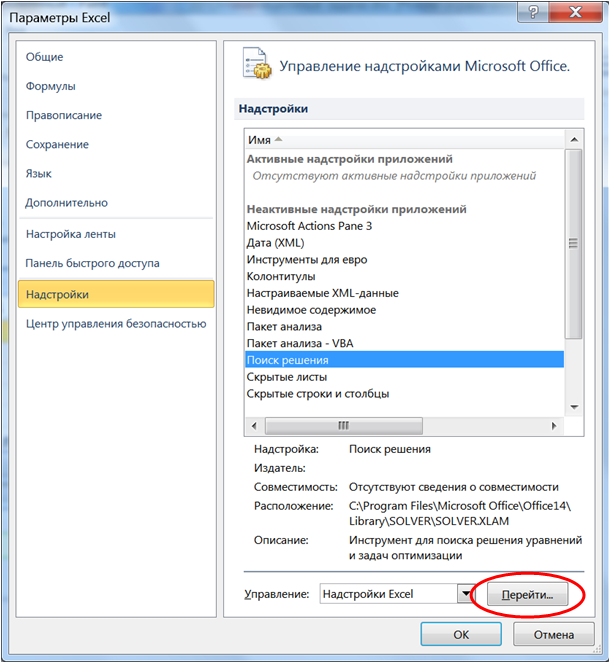
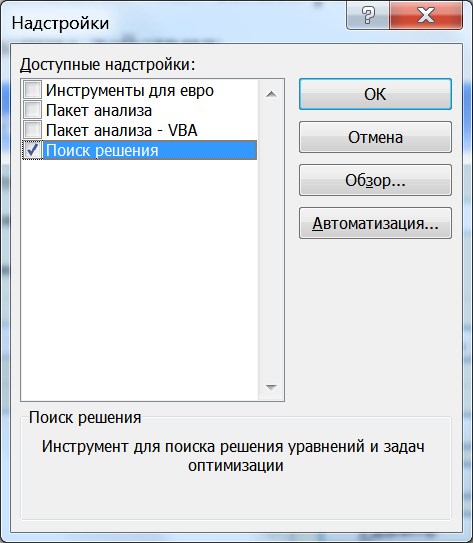
Рис. 7. Установка программы «Поиск решения» в Excel 2007/2010.
После его вызова появится окно Поиск решения (рис. 8 для Excel 2003/2007 или рис. 9 для Excel 2010; по сути, эти интерфейсы программы «Поиск решения» практически совпадают), в котором нужно выполнить перечисленные ниже действия.
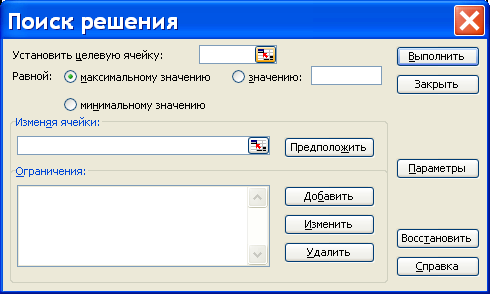
Рис. 8. Окно программы «Поиск решения » в Excel 2003/2007.

Рис. 9. Окно программы «Поиск решения » в Excel 2010.
1. В поле «Установить целевую ячейку» («Оптимизировать целевую функцию») нужно указать адрес ячейки целевого параметра (в нашем примере – прибыли Pr). Как и всюду в Excel, адрес указывается щелчком по соответствующей ячейке в таблице.
2. Указать критерий оптимизации, выбрав переключатель максимального или минимального значения (для задачи максимизации или минимизации, соответственно), или установить нужное значение целевого параметра (при решении уравнения). Мы устанавливаем переключатель максимума.
3. В поле «Изменяемые ячейки/переменные» указать все ячейки изменяемых (независимых) внутренних параметров. В нашем примере это вектор плана производства X.
4. Добавить ограничения. Для этого нажмите кнопку Добавить и в появившемся окне (рис. 10) выберите операцию (£, ≥, = или цел) и укажите её операнды (слева – ссылка на ячейку или диапазон параметра, справа – число или ссылку). На рисунке показано добавление ограничение нашей задачи С £ В (адреса диапазонов см. на рис. 1).
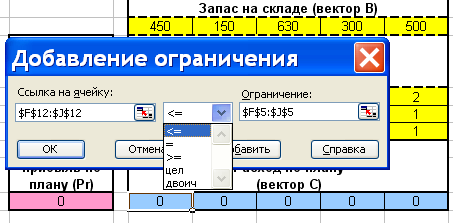
Рис. 8. Добавление ограничения.
Для добавления новых ограничений можно в этом же окне нажать кнопку Добавить. Добавив все ограничения, закройте окно нажатием кнопки ОК и вернитесь в окно Поиск решения. Для нашего примера оно может выглядеть, как на рис. 11.
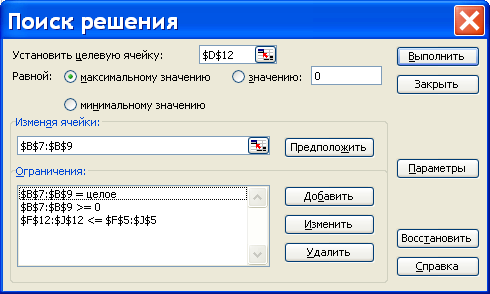
Рис. 11. Окно с моделью задачи оптимизации.
5. Введённые в этом окне данные называются моделью задачи оптимизации. Дополнительные параметры оптимизации можно установить с помощью кнопки Параметры. Для решения задачи нажмите кнопку Выполнить (Найти решение).
6. Результаты решения сразу появятся в таблице и в новом окне (рис. 12), которое в нашем случае сообщает об успешном решении задачи оптимизации. Нажав кнопку ОК, можно вернуться к исходному состоянию таблицы (без оптимального решения), если установлен флажок «Восстановить исходные значения», или к таблице, в которой сохранено найденное оптимальное решение.

Рис. 12. Результат работы программы Solver.
7. Сохранить модель. Excel помнит последнюю модель оптимизации, поэтому при работе с разными моделями (для одной или для разных задач) необходимо запомнить построенную модель, чтобы вернуться к ней, когда потребуется. Для этого нужно открыть окно Поиск решения (в нём откроется модель, см. рис. 11) и нажать в нём кнопку Параметры и в появившемся окне нажать кнопку Сохранить модель … (рис. 13 слева) или сразу нажать кнопку Загрузить/сохранить (рис. 9).
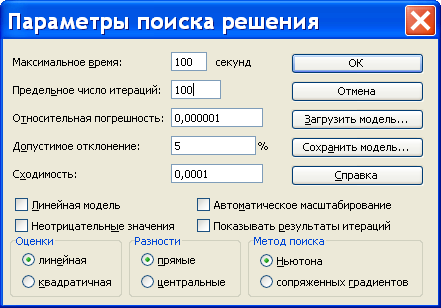
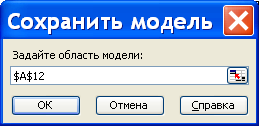
Рис. 13. Сохранение модели оптимизационной задачи.
В окне Сохранить модель (рис. 13 справа) нужно указать адрес, начиная с которого в столбик расположатся данные модели. Они займут три ячейки плюс по одной ячейки на каждое ограничение. В нашем случае это будет 6 ячеек. Нужно предусмотреть также заголовок модели. На рис. 14 слева показан, как выглядит модель в нашем примере (мы дали ей имя Модель 1), а справа – формулы, стоящие в этих ячейках.


Рис. 14. Сохранённая модель задачи.
В первой строке сохраняется критерий оптимизации и его оптимальное значение. Во второй – адреса изменяемых переменных (функция СЧЁТ выдаёт их количество). В следующих ячейках – ограничения. В последней ячейке – список параметров, указанных в окне Параметры поиска решения (рис. 13 слева).
Чтобы в дальнейшем использовать одну из сохранённых моделей, нужно в окне Параметры поиска решения (рис. 13 слева) нажать кнопку Загрузить модель … и в появившемся окне указать весь диапазон ячеек, занятых нужной моделью.
Задание 2. Индивидуальные варианты
В каждом варианте задаётся только количество видов продукции и видов используемых комплектующих. Названия этих видов вы должны придумать сами. Числовые значения векторов Р и В, а также матрицы R, могут быть заданы произвольно (но правдоподобно).
Варианты:
1) Видов продукции 5, комплектующих – 4.
2) Видов продукции 4, комплектующих – 5.
3) Видов продукции 5, комплектующих – 5.
4) Видов продукции 4, комплектующих – 4.
5) Видов продукции 5, комплектующих – 3.
6) Видов продукции 3, комплектующих – 5.
7) Видов продукции 3, комплектующих – 3.
8) Видов продукции 4, комплектующих – 3.
9) Видов продукции 3, комплектующих – 4.
10) Видов продукции 5, комплектующих – 6.