ОСОБЫЕ РЕЖИМЫ В ЦЕПЯХ ПЕРЕМЕННОГО ТОКА

Несинусоидальные токи

П р о г р а м м а

Причины возникновения несинусоидальных токов.

Сложение синусоидальных величин разной частоты на волновой диаграмме. Виды периодических кривых. Разложение периодических кривых на гармоники. Основная гармоника, высшие гармоники.

Действующее значение несинусоидального тока и напря­жения, коэффициент искажения (коэффициент гармоник). Мощность несинусоидального тока.

Электрические фильтры: схемы низкочастотных фильтров, резонансных заградительных полосовых фильтров и филь­тров высокой частоты.

 

Нелинейные цепи переменного тока

П р о г р а м м а

Основные понятия: нелинейные активные сопротивления, нелинейные индуктивные сопротивления (катушка со сталь­ным сердечником), нелинейные емкостные сопротивления (конденсаторы с сегнетоэлектриками). Причины широкого применения в технике нелинейных элементов.

Э. д. с., магнитный поток и ток в катушке со стальным сердечником; построение кривой тока в катушке при сину­соидальном напряжении по основной кривой намагничива­ния. Влияние гистерезиса и вихревых токов на ток в катуш­ке со стальным сердечником; построение кривой тока по кривой магнитного потока и петлей гистерезиса. Потери энер­гии в стали.

Катушка со стальным сердечником (холостой ход транс­форматора); схема замещения, векторные диаграммы с уче­том активного сопротивления обмотки и с учетом потока рас­сеяния. Понятие о дросселе насыщения в магнитном усили­теле.

 

Л а б о р а т о р н а я р а б о т а № 24

Исследование неразветвленной цепи переменного тока, содержащей катушку с ферромагнитным сердечником.

 

Переходные процессы в электрических цепях с сосредоточенными параметрами

П р о г р а м м а

 

Основные понятия: принужденный и переходный режимы; первый и второй законы коммутации. Включение цепи с ин­дуктивностью и активным сопротивлением на синусоидаль­ное напряжение: Заряд и разряд конденсатора на активное - сопротивление; графики тока и напряжения на конденсаторе.

Короткое замыкание цепи переменного тока с индуктивностью и активным сопротивлением, схема короткого замы­кания; график тока и напряжения, постоянная времени ко­роткозамкнутой цепи; периодическая и апериодическая (сво­бодная) составляющая тока короткого замыкания. Короткое замыкание цепи постоянного тока с индуктивностью и активным сопротивлением. Переходный процесс при отключении неразветвленной цепи постоянного тока с индуктивностью и активным сопротивлением; э. д. с. самоиндукции; явление автоэмиссии, характер отключающей аппаратуры.

 

Лабораторная работа № 25

Исследование - переходных процессов в цепи с емкостью и активным сопротивлением.

 

Электрические цепи с распределенными параметрами (длинные линии)

П р о г р а м м а

Основные понятия: цепи с сосредоточенными и распре­деленными параметрами; схема длинной линии; схема заме­щения однородной линии с потерями и без потерь. Рас­пространение электромагнитной волны с прямоугольным фронтом вдоль линии без потерь: различные случаи отраже­ния электромагнитной - волны от конца линии.

Вопросы для самопроверки при подготовке к экзамену по разделу «Особые режимы в цепях переменного тока»

[1]. Причины возникновения нёсинусоидальных напряжений и токов. Сложение на волновой диаграмме синусоидальных напряжений различных частот.

2. Подсчет полных сопротивлений токам разных частот в цепи с несинусоидальным напряжением и током.

3. Действующее значение несинусоидальных напряжений тока. Мощность несинусоидального тока.

4. Расчет электрической цепи с последовательным соеди­нением активного и индуктивного сопротивлений при несинусоидальном напряжении.

5. Расчет электрической цепи с последовательным соеди­нением , , и при несинусоидальном напряжении.

6. Понятие об электрических фильтрах: заградительные и полосовые фильтры; фильтры низкой и высокой частоты.

7. Кривые напряжения, тока и магнитного потока в катуш­ке с ферромагнитным сердечником.

8. Потери энергии от вихревых токов и гистерезиса. Оп­ределение эквивалентного синусоидального тока.

9. Катушка со стальным сердечником в цепи переменно­го тока; ее упрощенная векторная диаграмма. Потребляе­мая активная мощность.

 

10. Полная векторная диаграмма «катушки со стальным сердечником, составляющие тока и напряжения.

11. Устройство и «принцип действия однофазного транс­форматора. Режим холостого хода и рабочий режим транс­форматора.

12. Устройство трехфазного трансформатора и автотранс­форматора.

1З, Заряд конденсатора через резистор. Постоянная времени цепи. Графики зависимости тока и напряжения на кон­денсаторе от времена.

14. Разряд конденсатора через резистор. Постоянная вре­мени цели. Трафики зависимости тока и напряжения на кон­денсаторе от времени.

15. Короткое замыкание в цепи с индуктивностью и ак­тивным сопротивлением. 'Постоянная времени цепи. График зависимости тока переходного «процесса от времени.

16. Включение цепи с сопротивлением и индуктивностью а постоянное напряжение. Постоянная времени цепи. Гра­фик зависимости тока переходного процесса от времени.

17. Электрические цепи с сосредоточенными и распреде­ленными параметрами (основные понятия). Схема длинной линии.

18. Особенности и схема электрической цепи с распреде­ленными параметрами.

19. Распространение электромагнитной волны с прямо­угольным фронтом вдоль линии без потерь.

20. Различные случаи отражения электромагнитной вол­ны от конца линии.

 

Задание на домашнюю контрольную работу № 4

 

Задача 1. Три одинаковых приемника с сопротивлениями Z_А = Z_В = Z_С = (12+j16) Ом соединены звездой ипитаются от трехфазной сети с линейным напряжением U = 220 В.

Начертить схему цепи. Определить фазное напряжение U_ф; фазные I_ф и линейные I_лтоки; полную S, активную Р иреактивную Q мощности и коэффициент мощности cos техфазного потребителя.

Построить в масштабе m_u=40 В/см, m₁=2 A/см векторную диаграмму напряжений и токов.

Задача 2. В трехфазную сеть напряжением U_л = 380 В Людой включен приемник энергии мощностью Р = 6 кВт с коэффициентом мощности
cos =0,85 (индуктивный).

Начертить схему цепи. Определить фазное напряжение U_ф; фазные I_ф и линейные I_лтоки; полную S, активную Р иреактивную Q мощности и коэффициент мощности cos техфазного потребителя.

Построить в масштабе m_u=40 В/см, m₁=2 A/см векторную диаграмму напряжений и токов.

Задача 3. В трехфазную четырех проводную сеть напря­жением U_Л =380 В звездой включены три группы ламп на­каливания. Сопротивление каждой лампы R_Л = 440 Ом. Чис­ло ламп в каждой фазе n_А=20, n_В = 30, n_С = 40; лампы в фазах соединены параллельно.

Начертать схему цепи. Опреде­лить фазное напряжение U_ф; фазные сопротивления R_А, R_В, R_С фазные I_Ф и линейные I_л токи; активную мощность Р всех трех фаз.

Построить в масштабе m_u=50 В/см, m₁=5 A/см векторную диаграмму напряжений и токов; графически. (из векторной диаграммы) определить ток в нейтральном (нулевом) про­воде /₀. *

Задача 4. В трехфазную четырех проводную сеть напря­жением U_Л=380 В звездой включены приемники энергии. Мощность приемников в фазе
А-Р_А=1,5 кВт; в фазе А-Р_В = 2,0 кВт; в фазе C-P_c=1,0 кВт. Для всех приемни­ков cos =1.

Начертить, схему цепь. Определить фазное напряжение U_ф, фазные I_ф и линейные I_Л токи; активную мощность трех, фаз.

Построить в масштабе m_u=50 В/см, m₁=2 A/см векторную диаграмму напряжений и токов; графически (из векторной диаграммы) определить ток в нейтральном нулевом провес де Iо.

Задача 5. В трехфазную сеть напряжением U _л = 220 В включен двигатель, потребляющий мощность Р=9 кВт. Обмотка двигателя соединена звездой. Линейный ток двигателя I_л =50 А.

Начертить схему цели.

Определить фазное напряжение U_ф; полное z_ф активное R_Ф и -индуктивное x_LФ сопротивления фазы; коэффициент мощности cos : полную Sи реактивную Qмощности дви­гателя.

Построить в масштабе m_u=40 В/см, m₁=20 A/см векторную диаграмму напряжений и токов.

Задача 6. В трехфазную сеть напряжением U_л = 220 В включенном треугольником потребитель мощностью Р=10 кВт.

Начертить схему цепи. Определить фазное напряжение фазный U_Ф и линейный I_Л ток потребителя; полную S и реактивную Q мощность -потребителя.

Построить в масштабе m_u=50 В/см, m₁=210 A/см векторную диаграмму напряжений и токов.

Задача 7. В трехфазную сеть с линейным напряжением U_Л = 220 В включены треугольником три разные группы ламп. Мощность ламп в фазах составляет: Р_АВ = 4,4 кВт, Р_ВС = 2,2 кВт, Р_СА = 3,3 кВт.

Начертить схему цепи. Определить фазное напряжение фазные токи I_АВ, I_ВС I_САи мощность Р, потребляемую всеми лампами.

Построить в масштабе m_u=50 В/см, m₁=5 A/см векторную диаграмму напряжений и токов. Пользуясь масштабом найти по векторной диаграмме значения токов в линейных I_А, I_Вб I_С.

Задача8. В трехфазную сеть напряженнем U_Л = 380 Включен двигатель. Обмотка двигателя соединена треугольником, Полное сопротивление каждой фазы обмотки z_Ф = 30 Ом, коэффициент мощности двигателя cos . Начертить схему цепи. Определить активную мощность Р, фазное напряжение U_Ф фазный и линейный активное R_Ф и индуктивное x_LФсопротивления фазы.

Построить в масштабе m_u=100 В/см, m₁=4 A/см векторную диаграмму напряжений и токов.

Задача 9. В трехфазную сеть напряжением U_Л = 660 Включенытреугольником три катушки индуктивности. Сопротивление каждой катушки R = 24 Ом, x_L = 7 Ом.

Начертить схему цепи. Определить фазное напряжение U_Ф и линейный I_л токи; полную S, активную Р иреактивную Q мощности цели; коэффициент мощности цепи cos .

Построить в масштабе m_u=100 В/см, m₁=10 A/см векторную диаграмму напряжений и токов.

Задача 10. В трехфазную сеть 'Напряжением U_Л = 220 В включены три группы ламп накаливания, которые соединены треугольником. Мощность каждой лампы Р_л=50 Вт. Числа ламп в фазах: n_АВ = 15, n_ВС = 10, n_СА20 ламп; лампы в фазах соединены параллельно.

Начертить схему цепи. Определить фазное напряжение Uф, фазные токи, активную мощность всех ламп.

Построить в масштабе m_u=40 В/см, m₁=1 A/см векторную диаграмму напряжений и токов. Графически (по векторной диаграмме) определить значения линейных токов I_А, I_B, I_C.

Задача 11. Для условий задачи 1 определить, какими будут фазные напряжения и токи при перегорании предохрани­теля в линейном проводе А. Построить для этого случая векторную диаграмму напряжений и токов в масштабе m_u=40 В/см, m₁=2 A/см.

Задача 12. Для условий задачи 1 определить, какими бу­дут фазные напряжения и токи при коротком замыкании фазы В.

Построить для этого случая в масштабе m_u=40 В/см, m₁=5 A/см векторную диаграмму напряжений и токов.

Задача 13. Для условий задачи 3 определить, какими бу­дут фазные напряжения и токи при коротким замыкании фазы А и отключенном нейтральном ( нулевом ) проводе.

В Построить для этого случая в масштаб m_u=5 В/см, m₁=10 A/см векторную диаграмму напряжений и токов.

Задача 14. Для условий задачи 8 определить, какими будут фазные напряжения, фазные и линейные токи при перегорании предохранителя в проводе А.

В Построить для этого случая в масштаб m_u=50 В/см, m₁=3 A/см векторную диаграмму напряжений и токов.

Задача 15. Для условий задачи 9, определить, какими будут фазные напряжения, фазные и линейные токи при обрыве линейного провода.

В Построить для этого случая в масштаб m_u=100 В/см, m₁=5 A/см векторную диаграмму напряжений и токов.

Задача 16. К цепи, состоящей из последовательно включенных сопротивления R = 7 Ом, индуктивности L = 9,55 мГ и емкости С = 118 мкФ, приложено несинусоидальное напряжение u =(200+-35.25sin +14,85sin3 ) В. Частота f₁ =50 Гц.

Начертить схему цепи. Определить действующие значения синусоидальных напряжения U и тока I, а также коэффициент цепи.

Задача 17. Последовательная цепь, состоящая из резистора сопротивлением R=12 Ом и индуктивного сопротивления X_L = 5 Ом подключена к источнику электрической энергии с несинусоидальным напряжением, изменяющимся по закону u = (183,3sin +70,5sin5 ) В.

Значение сопротивлений даны для первой гармоники.

Начертить схему цепи. Определить действующие значение несинусоидальных тока I и напряжения U. а также коэффициент цепи.

Задача 18. Последовательная цепь, состоящая из резисторов сопротивлением R = 12 Ом и емкостного сопротивления X_C =27 Ом, подключена к источнику электрической энергии с несинусоидальным напряжением, изменяющимся по закону u = (200+141sin +28,23 ) В.

Значение сопротивлений даны для первой гармоники.

Начертить схему цепи. Определить действующие значение несинусоидальных тока I и напряжения U. а также коэффициент цепи.

Задача 19. К цепи, состоящей из последовательно включенным резистора R=8 Ом и конденсатора С=532 мкФ, при несинусоидальным напряжение
и = (310_,2sin +16,92sin2 ) В. Частота первой гармоники f₁ =50 Гц. Начертить схему цепи. Определить действующие значение несинусоидальных тока I и напряжения U. Активную Р и полную S мощности, а также также коэффициент цепи.

Задача 20. К цепи, состоящей из последовательно соедененных активного R= 12 Ом, индуктивного x_L=10 Ом и x_C = 26 Ом сопротивлении приложено н несинусоидальным напряжение u = (564sin +58,8sin2 ) В. Величины сопротивлений заданы для первой гармоники.

Начертить схему цепи. Определить действующие значение несинусоидальных тока I и напряжения U. а также коэффициент цепи.

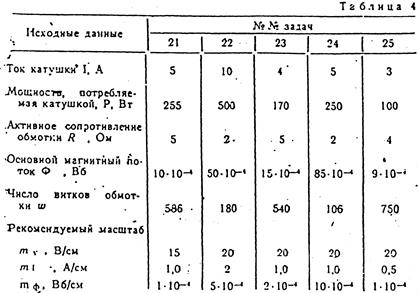
Задачи 21—25; Катушка со стальным сердечником вклю­чена в сеть переменного тока с напряжением U и частотой f=50 Гц. Ток в обмотке -катушки I; число витков обмотки , -активное сопротивление обмотки R_К. Мощность, потребляе­мая катушкой, Р.

В сердечнике катушки возбуждается основной максималь­ный магнитный поток Фм, при этом лоток рассеяния Фр составляет 10% от Ф_м. Начертить схему.

Определить: потери мощности в обмотке катушки Р_м и в стали Р_ст активную I_а и намагничивающую составля­ющие тока I; э. д.с. E, индуктируемую в обмотке за счет из­менения основного магнитного потока, и э. д.с. Е_P — за счет изменения потока рассеяния; тангенс угла потерь в
стали tg

Построить в масштабе полную векторную диаграмму катушки. По векторной диаграмме найти напряжение U, при­ложенное к катушке. Определить «коэффициент мощности катушки cos .

Рассчитать параметры последовательной электрической схемы замещения катушки с сердечникам (x_P, R_СТ, х_СТ) и на чертить эту схему.

Исходные данные задач 21—25 приведены в табл. 4.

Задача 26. Конденсатор емкостью С=1 мкФ, соединенный последовательно с резистором, сопротивление которого R= 5 МОм заряжается от сети с постоянным напряжением U = 100 В.

Начертить схему цепи. Определить постоянную времени цепи значения зарядного тока и напряжения на обкладках конденсатора для моментов времени t = 0; ; 2 ; 3 ; 4 ;

Построить в масштабе кривые u_c=f(t) и i_зар = f₁(t).

Задача 27. Конденсатор емкостью С = 5 мкФ, заряженный предварительно до напряжения U = 110 В, разряжается через резистор, сопротивление которого R= 5 МОм. Начертить схему цепи. Определить постоянную времени и значения разрядного тока и напряжения на конденсаторедля моментов времени: t = 0; ; 2 ; 3 ; 4 ; 5 ;.

Построить в масштабе кривые u_c=f(t) и i_зар = f₁(t).

Задача 28. Катушка с активным сопротивлением R=10 Ом и индуктивностью L=0,2 Г замыкается накоротко. Ток в котушке до короткого замыкания был равен I₀ = 20 А_. Начертить схему цепи. Определить постоянную времени и значения разрядного тока и напряжения на конденсаторедля моментов времени: t = 0; ; 2 ; 3 ; 4 ; 5 ;.

Построить в масштабе кривые i_кз = f(t).

Задача 29. Катушка с активным сопротивлением R = 6 Ом и индуктивностью L = 0.3 Г включается в сеть с постоянным напряжением
U = 60 В. Начертить схему цепи. Определить постоянную времени и значения разрядного тока и напряжения на конденсаторедля моментов времени: t = 0; ; 2 ; 3 ; 4 ; 5 ;.

Построить в масштабе кривые u_c=f(t) и i_зар = f₁(t).

Задача 30. Конденсатор емкостью С = 30 мкФ, соединен поледовательно с резистором, сопротивление которого R = 0,5 МОм, заряжается от сети с постоянным напряжением U=10 В. Определить постоянную времени цепи и значение зарядного тока и напряжения на конденсаторе для моментов времени t = 0; ; 2 ; 3 ; 4 ; 5 ;.

Начертить схему цепи. Построить в масштабе u_c=f₁(t) и i_зар = f(t).

Ответы к задачам контрольной работы № 4

 

Методические указания

к выполнению домашней контрольной работы №4

 

Задачи 1 — 15 посвящены расчету трехфазных цепей переменного тока. Для их решения необходимо знание онованых соотношений между линейными и фазными напряжениями и токами, формул мощности трехфазного потребителя принципов расчета трехфазных цепей и построения векторных диаграмм (Частоедов, §§ 15.1—15.8). Рассмотрим при меры.

Пример 24

Три одинаковые катушки включены звездой в трехфазную сеть с линейным напряжением U_Л = 380 В (рис. 63) Активное сопротивление каждой катушки R = 15 Ом. индуктивное x_L=20 Ом. Определить фазное напряжение. U_Ф; фазный I_Ф линейный I_л токи; полную S, активную Р и реак-

тивную Q мощность и коэффициент мощности cos трехфазного потребителя.

Построить в масштабе ; векторную диараму напряжений и токов.

Решение

1. Поскольку задана равномерная однородная нагрузка фаз, то даже при отсутствии нулевого провода фазные напряжения равны

2. Полное сопротивление каждой фазы

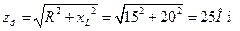
3. Токи фаз (они же линейные)

4. Коэффициент мощности вазы (а т.к. нагрузка фаз равномерная и однородная, то и всего трехфазного потребителя)

Следовательно ;

5. Мощности трехфазного потребителя:

Полная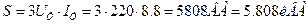

Активная

Реактивная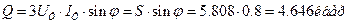

6. Строим векторную диаграмму (рис. 64)

Длины векторов фазных напряжений в масштабе

будут равны

Длины векторов фазных токов в масштабе

Будут равны

В начале откладываем векторы фазных напряжений.Вектор откладывается вертикально вверх, вектор отстает от вектора на 120 градусов, а вектор в свою очередь отстает от вектора на 120 градусов. Соединив концы векторов фазных напряжений, получим треугольник линейных напряжений .

 

 

Поскольку нагрузка фаз активно-индуктивная, то векторы фазных токов будут отставать от векторов фазных напряжений на угол =53° (соs =0,6).

Пример 25

Для условий примера 24 определить, какими будут фазные напряжения и токи при перегорании предохранителя в линейном проводе В. Построить для этого случая в масштабе , векторную диаграмму напряжений и токов.

Решение

1. При перегорании предохранителя в линейном проводе. В схема приобретает вид, показанный на рис. 65. Нагрузка из трехфазной превращается в однофазную: сопротивления фаз А и С соединены последовательно и включены на линейное напряжение .

2. Фазные напряжения

т.к. ток в этой фазе равен нулю,

, т.к. сопротивление фаз А и С соединены последовательно и включены на линейное напряжение =380В, которое делиться между фазами пополам (). Фазные напряжения уменьшились при обрыве провода В.

3. 3.Полное сопротивление фазы

4.

5. и двух фаз, соединенных последовательно

6.

7. ,

8.

9.

10. (арифметическое сложение сопротивлений возможно только равномерной однородной нагрузке)

11. 4. Фазные (они же линейные) токи:

12.

13. ; или

14. Фазные токи уменьшились.

15. 5. Строим векторную диаграмму (рис. 66)

16. Длина вектора линейного напряжения в масштабе

17. будет равна

Длина вектора фазного (линейного) тока в масштабе

равна

Поскольку нагрузка фаз активно-индуктивная, то вектор фазного (линейного) тока должен отставать от вектора напряжения на угол =53

 

Пример 26

В трехфазную четырех проводную сеть напряжением 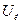= 220 В звездой включены три резистора (рис. 67). Сопротивления резисторов 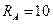Ом; Ом; Ом. Определить фазное напряжение фазные и линейные токи; активную мощность всех трех фаз.

Построить в масштабе 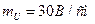,; векторную диаграмму напряжений и токов.Графически(из векторной

 

диаграммы) определить ток в нейтральном (нулевом) проводе

Решение

1.Поскольку задана трехфазная четырех проводная система, т. е. есть нулевой провод, то фазные напряжения:

2. Токи фаз (они же линейные):

3. Активная мощность трех фаз:

4.Посторение векторной диаграммы:

Длины векторов фазных напряжений в масштабе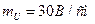

длины векторов фазных токов в масштабе

;

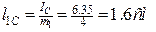
векторы фазных токов совпадают с векторами соответству­ющих фазных напряжений, т. к. нагрузка фаз активная.

Вектор тока в нейтральном (нулевом) проводе согласно первому закону Кирхгофа равен сумме векторов фазных. токов, т. е. . Сложение векторов фазных токов и построение вектора выполнено на векторной диаграмме

(рис. 68). Величину тока находим, измерив длину его вектора и пользуясь масштабом:

Пример 27

Для условий примера 26 определить, какими будут фазные напряжения и токи при коротком замыкании фазы С и отключенном нейтральном (нулевом) проводе.

 

Построить в масштабе ; векторную диаграмму напряжений и токов.

 

Решение

1. При коротком замыкании фазы С -и отключенном ну­левом проводе схема приобретает вид, показанный на рис. 69. Линейный провод С непосредственно соединяется с нулевой точкой трехфазного потребителя.

2. Фазные напряжения

(т.к. R_C=0);

;

.

 

3. Фазные (они же линейные) токи:

;

;

- по первому закону Кирхгофа.

Величину найдем графически (из векторной диаграммы).

 

 

 

4.Строим векторную диаграмму (рис. 70). Длина векторов линейных напряжений в масштабе ;

Длины векторов фазных токов в масштабе ; ;

 

Векторы фазных токов I_А' и Iв' совпадают с векторами фазных напряжений U_А' и U_в' (активная нагрузка фаз).

 

5.Вектор тока в линейном проводе С согласно первому закону Кирхгофа равен сумме векторов фазных токов c'= a'+ в'. Сложение векторов фазных токов и построение вектора c' выполнено на векторной диаграмме (рис. 70).Величину тока c' найдем, измерив длину его вектора и пользуясь масштабом:

c'= ₁c' m₁≈6.5 5=32.5 A.

Пример 28

Трехфазный двигатель мощностью Р=15 кВт, при соs =0,87 питается от сети с линейным напряжением U_л=380 В. Обмотки двигателя соединены треугольником

(рис. 71). Оп­ределить фазное напряжение Uф; фазный Iф и линейный I_л токи; полное сопротивление фазы полную Zф, полную S и реактивную Q мощности двигателя.

 

Построить в масштабе mu=100В/см; m₁=5 A/см векторную

диаграмму напряжений и токов.

 

 

Решение

1. При соединении треугольником фазное напряжение равно линейному, т.е

Uф=Uл=380 В.

 

2. Из формулы мощности находим фазный ток двигателя

 

3. Полное сопротивление фазы по закону Ома

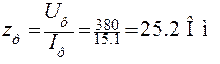
4. Линейный ток при равномерной нагрузке фаз

5. Полная мощность двигателя

6. Реактивная мощность двигателя

 

7. Построение векторной диаграммы.

Длина векторов фазных (линейных) напряжений в масштабе:

Длина векторов фазных токов в масштабе:

При построении векторной диаграммы вначале откладываем три вектора линейных (фазных) напряжений со сдвигом относительно друг друга на 120 градусов. Векторы фазных токов отстают от векторов фазных напряжений на угол =30 (cos =0.87),

Нагрузка активно-индуктивная. Соединив концы векторов фазных токов,получаем треугольник линейных токов; при этом векторы линейных токов являются разностью векторов соответствующих фазных токов:

; ;

Векторная диаграмма приведена на рис 72.

 

 

Пример 29

 

Для условий примера 28 определить, какими будут фазные напряжения, фазные и линейные токи при перегорании предохранителя в линейном проводе В.

 

 

Построить в масштабе и векторную диаграмму напряжений и токов.

 

Решение

 

1. В случае перегорания предохранителя в линейном проводе. В (обрыве линейного провода) создается режим однофазного питания: между линейными проводами А и С образуются две параллельные ветви. В первую входит сопротивление ,во вторую 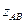и , соединенные последовательно(рис 73)

 

 

 

2. Токи фаз:

- в этой фазе сохранился прежний ток;

Где - полные сопротивления фаз двигателя (см. расчет в предыдущем примере 28).

 

Сопротивление находится арифметическим сложением лишь при равномерном и одномерной нагрузке,как в данном примере.

В противном случае

Знак «+» относится к однородным реактивным сопротивлениям, а знак «-«- к неоднородным.

3. Напряжения фаз

- сохранилось прежнее

;

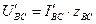
В данном случае (поскольку )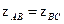

4. Линейные токи

Токи и можно арифметически складывать только в случае, если они имеют одинаковый по величине и знаку угол сдвига по отношению к фазному напряжению. В противном случае должны складываться векторы этих токов.

5. Векторная диаграмма (рис 74.)

Длина вектора фазного (линейного) напряжения в масштабе

; длина векторов фазных токов в масштабе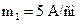

;

Векторы фазных токов отстают от вектора фазного напряжения на угол

Нагрузка активно-индуктивная.

6. Вектор линейного ток