|
Наплывы краски | || |
Пузыри | | | 5. Проанализируйте контрольный листок для регистрации интервальных данных, которая проводилась для пяти интервальных значений по шести производственным линиям: Контрольный листок Класс Границы класса Результаты измерений Всего: Линия 1 Линия 2 Линия 3 Линия 4 Линия 5 Линия 6 0,51-5,50
| | || ||
| 5,51-10,50 || ||
||
|| || 10,51-15,50 | || ||
|| | 15,51-20,50
| || |
Nbsp; Практическое занятие №3. ПОСТРОЕНИЕГИСТОГРАММ ДЛЯ КОНТРОЛЯ КАЧЕСТВА Цель занятия: сформировать у студентов теоретическое знание о гистограммах и практическое умение по их построению и анализу. Основу любого исследования составляют данные, полученные в результате контроля и измерения одного или нескольких параметров изделия (характеристики качества). Во всех отраслях промышленности требуется проведение анализа точности и стабильности процесса, наблюдение за качеством продукции, отслеживание существенных показателей производства. Путем измерения соответствующих параметров необходимыми средствами получают ряд данных, представляющих собой неупорядоченную последовательность значений параметра, на основе которых невозможно сделать корректные выводы. Поэтому для осмысления качественных характеристик изделий, процессов, производства (статистических данных) часто строят гистограмму распределения. Гистограмма – это инструмент, позволяющий зрительно оценить распределение статистических данных, сгруппированных по частоте попадания данных в определенный (заранее заданный) интервал. Гистограмма – это столбчатая диаграмма, служащая для графического представления имеющейся количественной информации, собранной за длительный период времени (неделя, месяц, год и т.д.), которая дает важную информацию для оценки проблемы и нахождения способов ее решения. Гистограмма применяется главным образом для анализа значений измеряемых параметров. Благодаря простоте построения и наглядности гистограммы нашли применение в различных областях: — для анализа сроков получения заказа (за контрольный норматив принимается срок поставки согласнодоговору); — для анализа времени реагирования группы обслуживания с момента получения заявки от клиента; — для анализа значений показателей качества, таких как размеры, масса, механические характеристики, химический состав, выход продукции и т. д. при контроле готовой продукции, при приемочном контроле, при контроле процесса в самых разных сферах деятельности; — для анализа числа бракованных изделий, числа дефектов, числа поломок. Полученная в результате анализа гистограммы информация может быть легко использована для построения и исследования причинно-следственной диаграммы, что повысит обоснованность мер, намеченных для улучшения процесса. Последовательность построения гистограммы: 1. Необходимо все имеющиеся результаты измерений разбить на несколько выборок с равным количеством данных в каждой: № выборки Результаты измерений 1-10 2,510 2,517 2,522 2,510 2,511 2,519 2,532 2,543 2,525 2,522 11-20 2,527 2,536 2,506 2,541 2,512 2,515 2,521 2,536 2,529 2,524 21-30 2,529 2,523 2,523 2,543 2,519 2,528 2,543 2,538 2,518 2,534 31-40 2,520 2,514 2,512 2,534 2,526 2,530 2,532 2,526 2,523 2,520 41-50 2,535 2,523 2,526 2,525 2,532 2,522 2,502 2,530 2,522 2,514 51-60 2,533 2,510 2,542 2,524 2,530 2,521 2,522 2,535 2,540 2,528 61-70 2,525 2,151 2,520 2,519 2,526 2,527 2,522 2,542 2,540 2,528 71-80 2,531 2,545 2,524 2,522 2,520 2,519 2,519 2,529 2,522 2,513 81-90 2,518 2,527 2,511 2,519 2,531 2,527 2,529 2,528 2,519 2,521 2. По каждой выборке необходимо найти наибольшее и наименьшее значения: № выборки Результаты измерений max в строке min в строке 1-10 2,510 2,517 2,522 2,510 2,511 2,519 2,532 2,543 2,525 2,522 2,543 2,510 11-20 2,527 2,536 2,506 2,541 2,512 2,515 2,521 2,536 2,529 2,524 2,541 2,506 21-30 2,529 2,523 2,523 2,543 2,519 2,528 2,543 2,538 2,518 2,534 2,543 2,518 31-40 2,520 2,514 2,512 2,534 2,526 2,530 2,532 2,526 2,523 2,520 2,534 2,512 41-50 2,535 2,523 2,526 2,525 2,532 2,522 2,502 2,530 2,522 2,514 2,535 2,502 51-60 2,533 2,510 2,542 2,524 2,530 2,521 2,522 2,535 2,540 2,528 2,542 2,510 61-70 2,525 2,551 2,520 2,519 2,526 2,527 2,522 2,542 2,540 2,528 2,551 2,520 71-80 2,531 2,545 2,524 2,522 2,520 2,519 2,519 2,529 2,522 2,513 2,545 2,513 81-90 2,518 2,527 2,511 2,519 2,531 2,527 2,529 2,528 2,519 2,521 2,531 2,511 2,551 2,502 3. Вычисление выборочного размаха R = (наибольшее наблюдаемое значение) - (наименьшее наблюдаемое значение) Эти наибольшие и наименьшие значения могут быть легко получены следующим образом: сначала надо вычистить наибольшее и наименьшее значения в каждой строке таблицы исходных данных, а затем взять самое большое из максимумов и самое маленькое из минимумов. Это и будет максимум и минимум всех наблюдаемых значений. R = 2,551 - 2,502 = 0,049. 4. Определение размеров классов Размеры классов определяются так, чтобы размах, включающий максимальное и минимальное значения, делился на интервалы равной ширины. Для получения ширины интервалов R делят на 1, 2 или 5 (либо 10, 20, 50; 0,1, 0,2, 0,5 и т.д.), чтобы получилось от 5 до 20 интервалов равной ширины. Если возникают две возможности, используют более узкий интервал при числе наблюдений 100 и больше, и более широкий при 99 наблюдениях и меньше. 0,049:0,002 = 24,5, примем это равным 25, округляя до ближайшего целого числа. 0,049:0,005 = 9,8 - примем это равным 10, округляя до ближайшего целого числа. 0,049:0,010 = 4,9 - примем это равным 5, округляя до ближайшего целого числа. Таким образом, интервал класса оказался равным 0,005, поскольку при этом получается число интервалов между 5 и 20. 5. Подготовка бланка таблицы частот Готовится бланк, куда можно занести класс, среднюю точку, отметки частот, частоты и т.д. 6. Определение границ класса Границы интервалов определяются так, чтобы они включали наименьшее и наибольшее значения и лежат в основе таблицы частот. Сначала определяют нижнюю границу первого класса и прибавляют к ней ширину этого класса, чтобы получить границу между первым и вторым классами. При этом следует удостовериться, что первый класс включает наименьшее значение, и что его граничное значение приходится на середину принятой единицы измерения (т.е. на число 5 в следующем десятичном разряде). Далее, продолжая прибавлять найденный интервал к предыдущему значению для получения второй границы, затем третьей и т.д., можно удостовериться, что последний класс включает максимальное значение. В примере, границы первого класса следует положить равными 2,500-2,505, так, чтобы этот класс включал наименьшее значение 2,502. Тогда границы второго класса придется положить равными 2,505 - 2,510 и т.д. Все это представлено в таблице частот: № п/п Класс № п/п Класс 2,500-2,505 2,540-2,545 2,505-2,510 2,545-2,550 2,510-2,515 2,550-2,555 2,515-2,520 2,520-2,525 2,525-2,530 2,530-2,535 2,535-2,540 7. Вычисление середины класса Середина класса= Так, в примере, средняя точка первого класса = Средняя точка второго класса = и.т.д. Середины второго, третьего и последующих классов можно еще получить так: середина второго класса = середина первого класса + интервал класса; и т.д. 8. Получение частот. Необходимо отметить и посчитать частоты попадания каждого результата измерений в каждый интервал, используя наклонные черточки, и по этим данным построить гистограмму: № п/п Класс Середина класса. x Подсчет частот Частота, f 2,500-2,505 2,503 / 2,505-2,510 2,508 //// 2,510-2,515 2,513 ///// /// 2,515-2,520 2,518 ///// ///// //// 2,520-2,525 2,523 ///// ///// ///// ////// 2,525-2,530 2,528 ///// ///// ///// ///// 2,530-2,535 2,533 ///// ///// 2,535-2,540 2,538 ///// 2,540-2,545 2,543 ///// // 2,545-2,550 2,548 2,550-2,555 2,553 / ИТОГО 9. Построение гистограммы и выводы. На горизонтальную ось наносят границы классов, пользуясь интервалом класса как основанием постройте прямоугольник, высота которого соответствует частоте этого класса. Нанесите на график линию, представляющую среднее арифметическое, а также линии, представляющие границы допуска, если они есть. На чистом поле гистограммы укажите происхождение ваших данных (период, в течение которого собирались данные и т.п.), число данных n, среднее арифметическое и стандартное отклонение s. Рис.3 Пример построения гистограммы
|
|
|
|
|
|
Типы гистограмм
Полезную информацию о характере популяции можно получить, взглянув на форму гистограммы. Формы, представленные на нижерасположенных рисунках типичны, и ими можно воспользоваться ими как образцами при анализе процессов:
а) Обычный тип (симметричный или колоколообразный). Среднее значение гистограммы приходится на середину размаха данных. Наивысшая частота оказывается в середине и постепенно снижается к обоим концам. Форма симметрична, встречается чаще всего.
б) Гребенка (мультимодальный тип). Классы через один имеют более низкие частоты. Такая форма встречается, когда число единичных наблюдений, попадающих в класс, колеблется от класса к классу или когда действует определенное правило округления данных.
в) Положительно скошенное распределение (отрицательно скошенное распределение). Среднее значение гистограммы локализуется слева (справа) от центра размаха. Частоты довольно резко спадают при движении влево (вправо) и, наоборот, медленно вправо (влево). Форма асимметрична. Такая форма встречается, когда нижняя (верхняя) граница регулируется либо теоретически, либо по значению допуска или когда левое (правое) значение недостижимо.
г) Распределение с обрывом слева (распределение с обрывом справа) Среднее арифметическое гистограммы локализуется далеко слева (справа) от центра размаха. Частоты резко спадают при движении влево (вправо) и, наоборот, медленно вправо (влево). Форма асимметрична. Это одна из тех форм, которые часто встречаются при 100 %-м просеивании изделий из-за плохой воспроизводимости процесса, а также когда проявляется резко выраженная положительная (отрицательная) асимметрия.
д) Плато (равномерное и прямоугольное распределения). Частоты в разных классах образуют плато, поскольку все классы имеют более или менее одинаковые ожидаемые частоты с конечными классами. Такая форма встречается в смеси нескольких распределений, имеющих различные средние.
е) Двухпиковый тип (бимодальный тип). В окрестностях центра диапазона данных частота низкая, зато есть по пику с каждой стороны. Такая форма встречается, когда смешиваются два распределения с далеко отстоящими средним значениями.
ж) Распределение с изолированным пиком. Наряду с распределением обычного типа появляется маленький изолированный пик. Это форма, которая появляется при наличии малых включений данных из другого распределения, как, скажем, в случае нарушения нормальное процесса, появления ошибки измерения или просто включения данных из другого процесса.
Контрольные вопросы:
1. Что такое гистограмма?
2. Для каких целей на практике используется гистограмма?
3. Назовите и кратко опишите виды гистограмм.
4. Каковы области применения гистограмм?
5. Опишите последовательность построения гистограмм.
Задания:
1. Постройте и проанализируйте гистограмму по имеющимся данным о температуре плавления битумно-латексной кровельной мастики и определите температурный интервал, в котором плавление мастики происходит в большинстве случаев:
| 77,2 | 86,4 | 86,0 | 76,3 | 68,4 | 63,9 |
| 77,5 | 93,4 | 75,8 | 91,1 | 74,9 | 61,8 |
| 91,5 | 74,1 | 86,9 | 78,0 | 72,2 | 84,2 |
| 83,5 | 88,5 | 78,6 | 82,4 | 76,6 | 86,3 |
| 61,9 | 71,8 | 69,8 | 77,1 | 82,4 | 76,7 |
| 58,7 | 68,3 | 73,0 | 82,4 | 78,7 | 69,8 |
| 87,9 | 62,4 | 67,7 | 63,8 | 74,8 | 71,3 |
| 80,2 | 77,3 | 76,0 | 91,5 | 51,2 | 74,8 |
| 77,4 | 80,9 | 67,0 | 72,5 | 85,9 | 66,6 |
| 77,8 | 84,1 | 79,2 | 88,4 | 72,3 | 69,4 |
| 91,7 | 79,0 | 101,0 | 74,7 | 71,5 | 97,7 |
| 87,0 | 70,6 | 89,3 | 87,5 | 95,6 | 85,9 |
| 54,5 | 75,6 | 70,9 | 83,7 | 72,9 | 92,6 |
| 93,9 | 77,1 | 76,3 | 94,9 | 78,5 | 82,9 |
| 73,8 | 79,1 | 90,8 | 92,7 | 61,6 | 80,6 |
2. Постройте гистограмму по имеющимся данным коэффициента деформации металла в процессе термообработки и определите интервал наибольшей деформации металла:
| 0,9 | 1,5 | 0,9 | 1,1 | 1,0 | 0,9 | 1,1 | 1,1 | 1,2 | 1,0 |
| 0,6 | 0,1 | 0,7 | 0,8 | 0,7 | 0,8 | 0,5 | 0,8 | 1,0 | 0,6 |
| 0,5 | 0,8 | 0,3 | 0,4 | 0,5 | 1,0 | 1,1 | 0,6 | 1,2 | 0,4 |
| 0,6 | 0,7 | 0,5 | 0,2 | 0,3 | 0,5 | 0,4 | 1,0 | 0,5 | 0,8 |
| 0,7 | 0,8 | 0,3 | 0,4 | 0,6 | 0,7 | 1,1 | 0,7 | 1,2 | 0,8 |
| 0,8 | 1,0 | 0,6 | 1,0 | 0,7 | 0,6 | 0,3 | 1,2 | 1,4 | 1,0 |
| 1,0 | 0,9 | 1,0 | 1,2 | 1,3 | 0,9 | 1,3 | 1,2 | 1,4 | 1,0 |
| 1,4 | 1,4 | 0,9 | 1,1 | 0,9 | 1,4 | 0,9 | 1,8 | 0,9 | 1,4 |
| 1,1 | 1,4 | 1,4 | 1,4 | 0,9 | 1,1 | 1,4 | 1,1 | 1,3 | 1,1 |
| 1,5 | 1,6 | 1,6 | 1,5 | 1,6 | 1,5 | 1,6 | 1,7 | 1,8 | 1,5 |
Практическое занятие №4. ПРИМЕНЕНИЕ СТРАТИФИКАЦИИ (РАССЛОЕНИЯ) ДЛЯ КОНТРОЛЯ КАЧЕСТВА ПРОДУКЦИИ
Цель занятия: сформировать у студентов теоретическое знание о стратификации и практическое умение по применению метода.
Одним из наиболее эффективных статистических методов, широко используемых в системе управления качеством, является метод стратификации или расслаивания.
Стратификация или расслоение (группировка) данных – инструмент, позволяющий произвести селекцию данных в соответствии с различными факторами.
В соответствии с этим методом производят расслоение данных, то есть группируют данные в зависимости от условий их получения и производят обработку каждой группы данных в отдельности.
Данные, разделенные на группы в соответствии с их особенностями, называют слоями (стратами), а сам процесс разделения на слои (страты) — расслаиванием (стратификацией).
Существуют различные методы расслаивания, применение которых зависит от конкретных задач. Например, данные, относящиеся к изделию, производимому в цехе на рабочем месте, могут в какой-то мере различаться в зависимости от исполнителя, используемого оборудования, методов проведения рабочих операций, температурных условий и т.д. Все эти отличия могут быть факторами расслаивания.
В производственных процессах часто используется метод расслоения по принципу «5М»: men, methods, materials, measure, machines (люди, методы, материалы, измерения, оборудование):
- по исполнителям (по квалификации, полу, стажу работы и т.д.);
- по способу производства (технологическому приему, месту производства, условиям производства);
- по материалу (по качеству сырья, партии, месту производства, сроку выпуска и т.д.);
- по измерению (по методу измерения, типу измерительных средств или их точности);
- по оборудованию и машинам (по новому и старому оборудованию, марке, конструкции, сроку службы и т.д.).
Однако пользоваться этим методом не так просто. Иногда расслаивание по, казалось бы, очевидному параметру не дает ожидаемого результата. В этом случае нужно продолжить анализ данных по другим возможным параметрам в поисках решения возникшей проблемы.
Рассмотрим пример: необходимо с помощью стратификации выявить строительные материалы, задержка поставки которых происходит чаще всего:
Задержка поставок строительных материалов
| Оформление заказа | Выполненные в срок | Выполненные с опозданием | Всего случаев |
| В соответствии с установленной датой | |||
| С опозданием | |||
| Всего случаев |
Чтобы разобраться с задержками поставок строительных материалов, необходимо провести более глубокий анализ. Для этого проведем расслоение по видам строительных материалов, которые составляют заказ.
| Оформление заказа | Выполненные в срок | Выполненные с опозданием | Всего случаев |
| Песок | |||
| Щебень | |||
| Гравий | |||
| Автоклавный ячеистый бетон | |||
| Рубероид | |||
| Всего случаев |
Вывод: более детальный анализ показал, что в основном задержки поставок происходят по следующим видам строительных материалов: рубероид, автоклавный ячеистый бетон, песок. Руководству следует обратить внимание на эти виды строительных материалов и принять меры по устранению их поставки (штраф, увеличение сроков поставок и др.).
Контрольные вопросы:
1. Что такое стратификация?
2. Что понимается под «расслоением по принципу «5М»?
3. Что такое «страт»?
4. По каким показателям проводят расслоение?
5. Для каких целей на практике используется стратификация?
Задания:
1 Имеются данные о браке при производстве строительных материалов в зависимости от переналадки оборудования. С помощью стратификации проанализируйте имеющиеся данные и сделайте вывод относительно типа (вида) оборудования, на котором производится бракованных материалов больше всего:
Зависимость наличия брака у изделия от переналадки оборудования
| Решение | Изделия имеет брак | Брак у изделия отсутствует | Всего изделий |
| Проведение периодической переналадки оборудования | |||
| Настройка оборудования отсутствует | |||
| Всего изделий |
| Решение | Изделия имеет брак | Брак у изделия отсутствует | Всего изделий |
| Станок А | |||
| Станок В | |||
| Станок С | |||
| Станок D | |||
| Станок Е | |||
| Всего изделий |
2. Имеются данные о необходимости инженерных коммуникаций в жилых домах. С помощью стратификации проанализируйте имеющиеся данные и сделайте вывод относительно инженерных сетей, требующих замены в первую очередь:
| Постепенная замена инженерных коммуникаций | Комплексная замена инженерных коммуникаций | Всего | |
| Первоочередная замена сильно изношенных коммуникаций, замена остальных – в более длительный срок | |||
| Комплексная замена инженерных сетей в короткие сроки, но недостаточно качественно | |||
| Всего случаев |
| Вид коммуникаций | Постепенная замена | Комплексная замена | Всего случаев |
| Система водоснабжения | |||
| Система отопления | |||
| Электрические сети | |||
| канализация | |||
| Система вентиляции и кондиционирования | |||
| Всего случаев |
3.Имеются данные о подаче отопления в жилые дома. С помощью стратификации проанализируйте имеющиеся данные и сделайте вывод о нарушении сроков подачи тепла в жилые дома по улицам:
| Подача отопления в срок | Подача отопления с опозданием | Всего | |
| В соответствии с установленной датой | |||
| С опозданием | |||
| Всего случаев |
| Подача отопления в домах на улицах | Подача отопления в срок | Подача отопления с опозданием | Всего случаев |
| Ул. Красноармейская | |||
| Пер.Университетский | |||
| Пр. Кировский | |||
| Пр Чехова | |||
| Пр Соколова | |||
| Пер. Крепостной | |||
| Всего случаев |
Практическое занятие №5. ДИАГРАММА РАЗБРОСА
Цель занятия: сформировать у студентов теоретическое знание о построении диаграммы разброса и практическое умение по ее построению и применению.
В процессе исследования часто приходится выяснять, существует ли зависимость между двумя различными параметрами процесса. Например, зависит ли качество готового изделия от качества исходных материалов, комплектующих деталей и узлов и т.д.
Для выяснения зависимости между показателями качества и основными факторами производства, а также корреляционной зависимости между факторами используют диаграммы разброса (рассеивания), которые также называются полем корреляции.
Диаграмма разброса (рассеивания) – это инструмент, позволяющий определить вид и тесноту связи двух рассматриваемых параметров процесса.
Диаграмма разброса представляет собой график, получаемый путем нанесения в определенном масштабе экспериментальных, полученных в результате наблюдений точек.
Координаты точек соответствуют значениям рассматриваемой величины и влияющего на него фактора.
Расположение точек на графике показывает наличие и характер связи между случайными величинами.
Диаграмма разброса позволяет наглядно показать характер изменения параметра качества во времени.
Использование диаграммы разброса в процессе контроля качества не ограничивается только выявлением вида и тесноты связи между парами переменных. Диаграмма разброса используется также для выявления причинно-следственных связей показателей качества и влияющих факторов.
Таким образом, диаграмма разброса дает возможность выдвинуть гипотезу о наличии или отсутствии корреляционной связи между двумя случайными величинами, которые могут относиться к характеристике качества и влияющему на нее фактору либо к двум различным характеристикам качества, либо к двум факторам, влияющим на одну характеристику качества.
Диаграмма разброса строится в следующей последовательности:
1. Собираются парные данные, которые по предположению являются взаимосвязанными. Желательно, чтобы таких парных данных было не менее 20-25. Это позволит более объективно установить зависимость между данными.
2. Составляется список данных. В списке данных для каждого измерения по порядку указываются значения парных данных.
3. Определяются максимальные и минимальные значения по каждому из типов парных данных.
4. Выбираются шкалы для осей диаграммы разброса на основании разницы между максимальным и минимальным значением каждого из типов парных данных. При необходимости (если отображаемые величины имеют малые размеры) могут применяться коэффициенты масштабирования шкалы.
5. Рисуются горизонтальная (Х) и вертикальная (Y) оси диаграммы. Шкала значений данных, обозначаемая на осях должна увеличиваться при подъеме по вертикальной оси и при движении вправо по горизонтальной. При исследовании корреляции между причиной и следствием (например, после применения диаграммы Исикавы) данные, характеризующие причину, откладываются по горизонтальной оси, а данные, характеризующие следствие - по вертикальной.
6. На диаграмму наносятся парные данные. Если для разных измерений получаются одинаковые значения данных, то для отделения данных друг от друга используется другое обозначение (например, точки и треугольники) или данные обозначаются рядом друг с другом.
Рассмотрим пример построения диаграммы разброса:
1. Цель построения: определить наличие и характер связи между случайными величинами, одна из которых представляет собой параметр технологического процесса, а другая – параметр качества изделия.
2. Для сбора данных разработан листок регистрации.
| х | у |
3. По полученным данным строится график, по одной оси которого - горизонтальной - откладываются значения х, по другой - вертикальной - значения у.
Диапазон изменения х от 17 до 68, поэтому ось х можно разбить в диапазоне от 10 до 80. Диапазон изменения у от 40 до 180. Разбиваем ось в пределах от 30 до 200.
На построенный таким образом график в масштабе наносим экспериментальные точки.
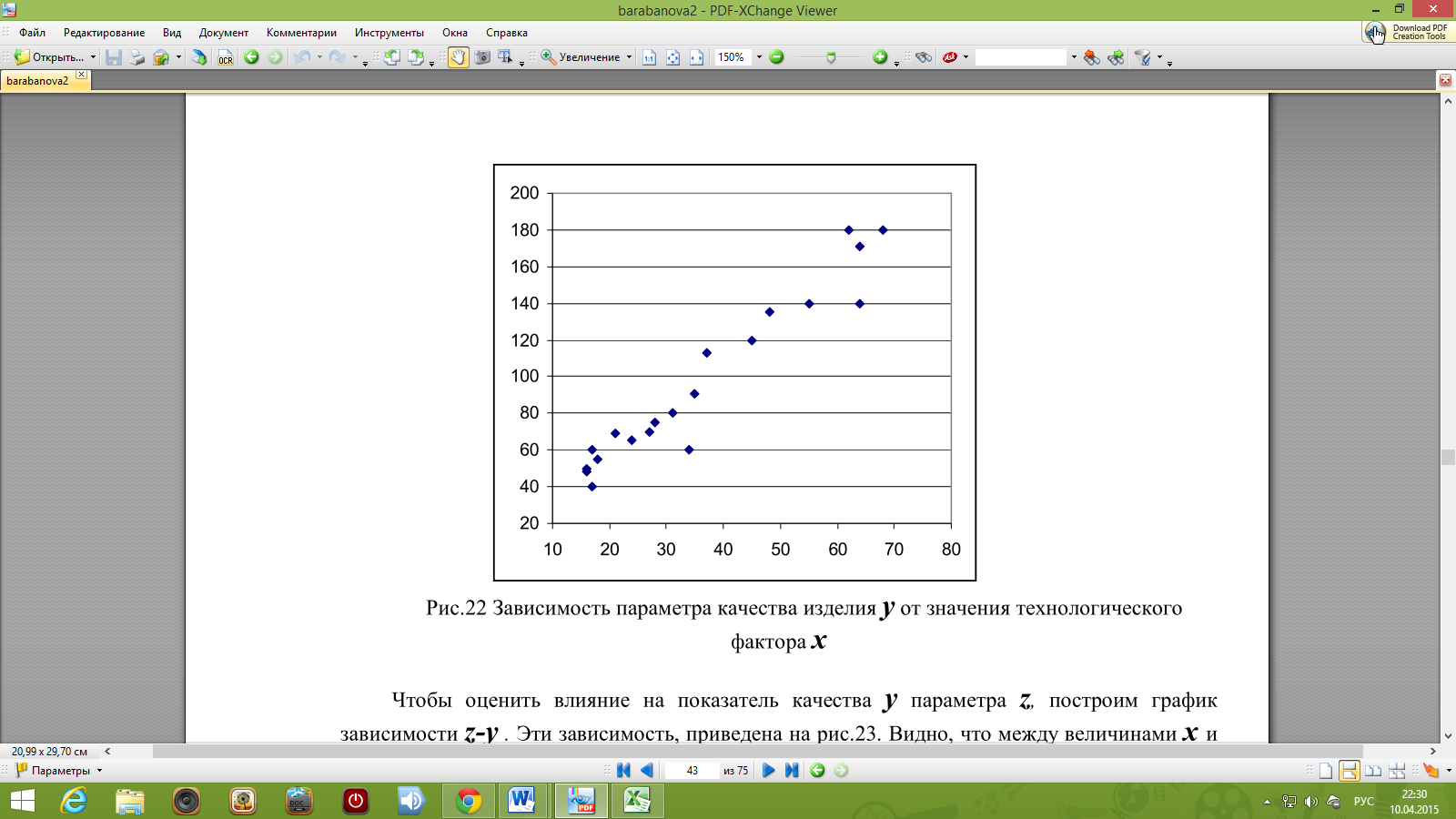
Рис.4 Зависимость параметра качества изделия у
от значения технологического фактора х
Вывод: облако точек вытянуто. В среднем при увеличении х происходит увеличение у. Следовательно, на основе полученных при наблюдениях результатов можно сделать вывод о наличии между данными величинами положительной корреляционной связи. То есть, технологический параметр х оказывает влияние на параметр качества изделия у.
Контрольные вопросы:
1. Дайте определение методу «Диаграмма разброса».
2. Что представляет собой диаграмма разброса?
3. Опишите последовательность построения диаграммы разброса.
4. Для каких целей на практике используется диаграмма разброса?
5. Какова область использования диаграммы разброса?
6. Что позволяют выявить диаграммы разброса?
Задания:
1. Постройте и проанализируйте диаграмму разброса по приведенным данным:
| № измерения | Износ инструмента (мм) | Диаметр отверстия (мм) |
| 1.1 | 11.6 | |
| 1.0 | 11.5 | |
| 0.9 | 11.3 | |
| 0.5 | 12.0 | |
| 0.6 | 11.9 | |
| 0.9 | 11.7 | |
| 1.3 | 11.2 | |
| 1.0 | 11.4 | |
| 1.1 | 11.5 | |
| 0.6 | 12.0 | |
| 0.2 | 12.3 | |
| 0.9 | 11.8 | |
| 0.5 | 11.9 | |
| 1.1 | 11.5 | |
| 1.0 | 11.4 | |
| 0.8 | 11.7 | |
| 0.8 | 11.6 | |
| 0.5 | 12.1 | |
| 0.1 | 12.5 | |
| 1.2 | 11.2 | |
| 0.7 | 11.9 | |
| 0.6 | 12.1 | |
| 0.9 | 11.9 | |
| 0.3 | 12.1 | |
| 0.9 | 12.0 |
Практическое занятие №6. РАСЧЕТ И ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВА БРАКОВАННЫХ ИЗДЕЛИЙ С ПОМОЩЬЮ ПОСТРОЕНИЯ ДИАГРАММЫПАРЕТО
Цель занятия: сформировать у студентов теоретическое знание о построении диаграммы Парето и практическое умение по их построению и применению.
В 1897 г. итальянский экономист В. Парето предложил формулу, показывающую, что общественные блага распределяются неравномерно. Эта же теория была проиллюстрирована на диаграмме американским экономистом М. Лоренцом. Оба ученых показали, что в большинстве случаев наибольшая доля доходов или благ (80%) принадлежит небольшому числу людей (20%).
Доктор Д. Джуран применил диаграмму М. Лоренца в сфере контроля качества для классификации проблем качества на немногочисленные, но существенно важные и многочисленные, но несущественные и назвал этот метод анализом Парето. Он указал, что в большинстве случаев подавляющее число дефектов и связанных с ними потерь возникают из-за относительно небольшого числа причин. При этом он иллюстрировал свои выводы с помощью диаграммы, которая получила название диаграммы Парето.
Диаграмма Парето - инструмент, позволяющий объективно представить и выявить основные факторы, влияющие на исследуемую проблему, и распределить усилия для ее эффективного разрешения.
Схема позволяет наглядно показать множество факторов, систематизированных в определенном порядке, что существенно облегчает поиски правильных решений.
Так как, согласно методу в большинстве случаев подавляющее число дефектов и связанных с ними материальных потерь возникает из-за относительно небольшого числа причин, то, выяснив причины появления основных дефектов, можно устранить почти все потери, сосредоточив усилия на ликвидации именно этих причин.
Различают два вида диаграмм Парето: по результатам деятельности и по причинам.
1 Диаграмма Парето по результатам деятельности предназначена для выявления главной проблемы и отражает следующие нежелательные результаты деятельности:
качество: дефекты, поломки, ошибки, отказы, рекламации, ремонты, возвраты продукции;
себестоимость: объем потерь, затраты;
сроки поставок: нехватка запасов, ошибки в составлении счетов, срыв сроков поставок;
безопасность: несчастные случаи, трагические ошибки, аварии.
2. Диаграмма Парето по причинам отражает причины проблем, возникающих в ходе производства, и используется для выявления главной из них:
рабочий: смена, бригада, возраст, опыт работы, квалификация, индивидуальные характеристики;
оборудование: станки, агрегаты, инструменты, оснастка, организация использования, модели, штампы;
сырье: изготовитель, вид сырья, завод-поставщик, партия;
метод работы: условия производства, заказы-наряды, приемы работы, последовательность операций.
Советы по построению диаграмм Парето
1. Воспользуйтесь разными классификациями и постройте много диаграмм Парето. Суть проблемы можно уловить, наблюдая явление с разных точек зрения, поэтому важно опробовать различные пути классификации данных, пока не выявятся немногочисленные существенно важные факторы, что и служит целью анализа Парето.
2. Нежелательно, чтобы группа «прочие» факторы составляла большой процент. Если такое происходит, значит объекты наблюдения расклассифицированы неправильно и слишком много объектов попало в одну группу. В этом случае надо использовать другой принцип классификации.
3. Если данные можно представить в денежном выражении, лучше всего это показать на вертикальных осях диаграммы Парето. Если нельзя оценить существующую проблему в денежном выражении, само исследование может оказаться неэффективным. Затраты – важный критерий изменений в управлении.
Как построить диаграмму Парето?
Этап 1 Решите какие проблемы надлежит исследовать и как собирать данные.
1) Какого типа проблемы вы хотите исследовать?
Пример: дефектные изделия, потери в деньгах, несчастные случаи.
2) Какие данные надо собрать и как их надо классифицировать?
Пример: по видам дефектов, по месту их появления, по процессам, по станкам, по рабочим, по технологическим причинам.
Примечание. Суммируйте остальные нечасто встречающиеся признаки под общим заголовком «прочие».
3) Установите метод и период сбора данных.
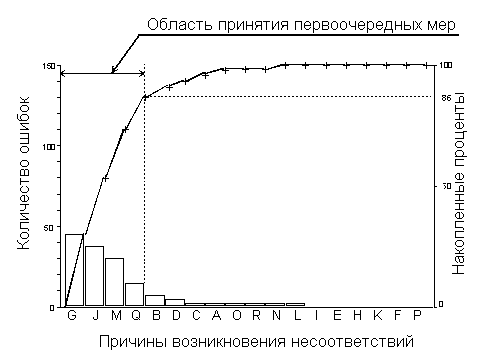
Рис. 5 Диаграмма Парето
Этап 2
Разработайте контрольный листок для регистрации данных с перечнем видов собираемой информации. В нем надо предусмотреть место для графической регистрации данных проверок:
| Типы дефектов | Группы данных | Итого |
| Трещины Царапины Пятна Деформация Разрыв Раковины Прочие | ||
| Итого |
Этап 3
Заполните листок регистрации данных и подсчитайте итоги.
Этап 4
Для построения диаграммы Парето разработайте бланк таблицы для проверок данных, предусмотрев в нем графы для итогов по каждому проверяемому признаку в отдельности, накопленной суммы числа дефектов, процентов к общему итогу и накопленных процентов
| Типы дефектов | Число дефектов | Накопленная сумма числа дефектов | Процент числа дефектов по каждому признаку в общей сумме | Накопленный процент |
| Деформация Царапины Раковины Трещины Пятна Разрыв Прочие | ||||
| Итого | - | - |
Этап 5
Расположите данные, полученные по каждому проверяемому признаку, в порядке значимости и заполните таблицу. Примечание. Группу «Прочие» надо поместить в последнюю строку вне зависимости от того, насколько большим получилось число, так как ее составляет совокупность признаков, числовой результат по каждому из которых меньше, чем самое маленькое значение, полученное для признака, выделенного в отдельную строку.
Этап 6
Начертите одну горизонтальную и две вертикальные оси.
1) Вертикальные оси:
(а) левая ось. Нанесите на эту ось шкалу с интервалами от 0 до числа, соответствующего общему итогу;
(б) правая ось. Нанесите на эту ось шкалу с интервалами от 0 до 100%.
2) Горизонтальная ось. Разделите эту ось на интервалы в соответствии с числом контролируемых признаков.
Этап 7
Постройте столбчатую диаграмму.
Этап 8
Начертите кумулятивную кривую (кривую Парето).
На вертикалях, соответствующих правым концам каждого интервала на горизонтальной оси, нанесите точки накопленных сумм (результатов или процентов) и соедините их между собой отрезками прямых.
Этап 9
1) надписи, качающиеся диаграммы (название, разметка числовых значений на осях, наименование контролируемого изделия, имя составителя диаграммы);
2) надписи, касающиеся данных (период сбора информации, объект исследования и место его проведения, общее число объектов контроля.
Советы по использованию диаграмм Парето
1. Если нежелательный фактор можно устранить с помощью простого решения, это надо сделать незамедлительно, независимо от того, каким бы незначительным он не был. Поскольку диаграмма Парето расценивается как эффективное средство решения проблем, значит, следует рассматривать только немногочисленные существенно важные причины. Однако, если относительно неважная причина устраняется простым путем, это послужит примером эффективного решения проблемы, а приобретенный опыт, информация, моральное удовлетворение окажут большое воздействие на дальнейшую процедуру решения проблем.
2. Не упускайте возможности составить диаграмму Парето по причинам. После выявления проблемы путем составления диаграммы Парето по результатам, важно определить причины возникновения проблемы, чтобы решить ее.
Рассмотрим проведение анализа Парето на примере: проблема: брак в производстве плит покрытия. Цели исследования:
1. Определить наиболее часто встречающиеся виды брака.
2. Определить виды брака, приводящие к наибольшим потерям.
Для построения диаграммы Парето составим таблицу, в которой отразим все необходимые данные.