ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«СМОЛЕНСКАЯ ГОСУДАРСТВЕННАЯ СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ»
Прикладная математика
Методические указания и контрольные задания
для студентов заочной формы обучения
(II семестр)
Составитель:
доцент кафедры ИТиВМ
Изотова О. А.
Смоленск - 2015
ВВЕДЕНИЕ
Настоящие методические указания предназначены для студентов-заочников и охватывают материал раздела курса высшей математики «Теория вероятностей и математическая статистика».
Методические указания содержат образцы решения некоторых задач и контрольные задания.
ПРИМЕРЫРЕШЕНИЯ ЗАДАЧ
Задачи по «Теории вероятностей»
1. Найти вероятность того, что при бросании игральной кости выпадет число большее 4.
Решение. Пусть А – событие: выпадет цифра большая 4. Пусть Еi – события: выпадет цифра под номером i. Тогда E 1, E 2, E 3, E 4, E 5, E 6 образуют группу элементарных событий. Количество всех элементарных событий n =6. Тогда А=Е5+Е 6, mA =2 и
2. Все натуральныечисла от 1 до 30 записаны на одинаковых карточках и помещены в урну. После тщательного перемешивания карточек из урны извлекается одна карточка. Какова вероятность того, что число на взятой карточке окажется кратным 5?
Решение. Обозначим через А событие «число на взятой карточке кратно 5». В данном испытании имеется 30 элементарных событий, из которых событию А благоприятствует 6 событий (числа 5, 10, 15, 20, 25, 30). Следовательно, 
3. В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди 6 взятых наудачу деталей 4 стандартных.
Решение. Общее число возможных элементарных событий испытания равно числу способов, которыми можно извлечь 6 деталей из 10, т.е. числу сочетаний из 10 элементов по 6 элементов
.
Определяем число событий, благоприятствующих событию А – «среди 6 взятых деталей 4 стандартных». Четыре стандартные детали из семи стандартных можно взять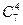 
способами, при этом остальные 6 – 4=2 детали должны быть нестандартными; взять же 2 нестандартные детали из 10 – 7=3 нестандартных деталей можно 
способами. Следовательно, число благоприятствующих событий равно 
.
Искомая вероятность равна отношению числа событий, благоприятствующих событию А, к числу всех элементарных событий:
.
4. Монета бросается два раза. Найти вероятность того, что хотя бы один раз выпадет «орел».
Решение. Пусть А – событие: хотя бы один раз выпадет «орел». Тогда А 1– событие: на 1-ом броске выпадет «орел», А 2– событие: на 2-ом броске выпадет «орел». Очевидно, что А=А 1 +А 2. Находим
5. В урне 40 шариков: 15 синих, 5 зеленых и 20 белых. Какова вероятность того, что из урны будет извлечен синий или зеленый шарик?
Решение. Пусть А – событие: из урны будет извлечен цветной шарик. Через А 1 – событие: извлечен синий шарик, А 2 – событие: извлечен зеленый шарик. Тогда А=А 1 +А 2, причем события А 1, А 2 несовместные. Получаем
6. Подбрасывается игральный кубик. Чуму равна вероятность того, что выпадет четное число очков?
Решение. Введем обозначения: А – событие: выпало четное число очков; Вk – события: выпало k очков (k= 1, 2, 3, 4, 5, 6). Событие А означает, что наступило хотя бы одно из событий: В 2, В 4, В 6, т.е. А=В 2 +В 4 +В 6. Поскольку события В 2, В 4, В 6несовместны, то можно воспользоваться формулой
при n= 3, учитывая, что Вk= 1/6 (k= 1, 2, 3, 4, 5, 6):
Замечание. Тот же результат получится и непосредственно по формуле 
7. В коробке 10 шаров: 4 белых и 6 черных. По-очереди извлекаются два шара. Найти вероятность того, что оба шара белые.
Решение. Пусть А – событие: оба шара белые. Тогда А 1 – событие: 1-ый шар белый, А 2 – событие: 2-ой шар белый. Очевидно, что А=А 1 А 2. Находим
8. В коробке 4 белых и 6 черных шаров. Два раза извлекают по одному шару и каждый раз кладут его обратно. Найти вероятность того, что оба раза вытащили белый шар.
Решение. Пусть А – событие: оба раза вытащили белый шар. Тогда А 1 – событие: 1-ый раз вытащили белый шар, А 2 - событие: 2-ый раз вытащили белый шар. Очевидно, что А=А 1 А 2, причем А 1 и А 2 независимые. Находим
9. Слово папаха составлено из букв разрезной азбуки. Карточки с буквами тщательно перемешаны. Четыре карточки извлекаются по очереди и раскладываются в ряд. Какова вероятность получить таким путем слово папа?
Решение. Обозначим через А, В, С, D соответственно события: извлечена первая, вторая, третья и четвертая буква слова папа из набора в 6 букв: а, а, а, п, п, х. Найдем вероятность событий: А, В/А, С/АВ, D/ABC.
; 
; 
; 
.
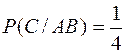Тогда при n= 4получаем
.
10. В магазин поступают изделия с трех фабрик: 20% - с фабрики №1, 30% - с фабрики №2, 50% - с фабрики №3. Фабрика №1 допускает 1% брака, фабрика №2 допускает 2% брака, фабрика №3 допускает 0,5% брака. Случайным образом выбирается одно изделие. Найти вероятность того, что оно бракованное.
Решение. Пусть А – событие: выбранное изделие бракованное. Через Hi обозначим события: изделие поступило с фабрики № i (i= 1,2,3), причем H 1, H 2, H 3 попарно несовместны. Тогда по формуле полной вероятности
11. Имеются две коробки с шарами. В 1-ой коробке содержится 99 белых шаров и 1 черный шар. Во 2-ой коробке содержится 1 белый шар и 99 черных шаров. Случайным образом выбирают коробку и достают один шар. Какова вероятность того, что это белый шар?
Решение. Пусть А – событие: достали белый шар. Тогда Н 1 – событие: выбрана коробка №1, Н 2 – событие: выбрана коробка №2. События Н 1 и Н 2 равновероятные, т.е.
.
Тогда
.
12. Производится 10 выстрелов по мишени. Вероятность попадания при каждом выстреле 0,9. Найти вероятность того, что будет ровно 7 попаданий.
Решение. В качестве испытания рассмотрим выстрел, в качестве события А – попадание в цель. Получим схему Бернулли из n= 10 испытаний, р= 0,9. Требуется найти P 10(7):
13. Испытывается 100 приборов. Вероятность того, что прибор не пройдет испытание равна 0,2. Найти вероятность того, что испытание пройдет не менее 72 приборов.
Решение. По условию n= 100, p= 0,2, q= 0,8. Требуется найти вероятность того, что испытание не пройдет 28 или меньше приборов, т.е. 
Тогда
В результате
14. В некоторой местности из каждых 100 семей 80 имеют холодильники. Найти вероятность того, что из 400 семей 300 имеют холодильники.
Решение. Вероятность того, что семья имеет холодильник, равна 
Т.к. n= 400 достаточно велико (npq= 64 
), то
Тогда
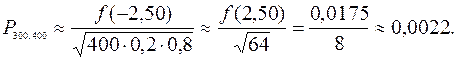
Замечание. Весьма малое значение вероятности 
не должно вызывать сомнения, т.к. кроме события «ровно 300 семей из 400 имеют холодильники» возможно еще 400 событий: «0 из 400», «1 из 400»,…, «400 из 400» со своими вероятностями. Все вместе эти события образуют полную группу, a значит, сумма их вероятностей равна 1.
15. Найти математическое ожидание дискретной случайной величины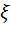 
, закон распределения которой задан таблицей
|
| |||||
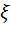
| р | 0,1 | 0,2 | 0,4 | 0,2 | 0,1 |
Решение. Воспользуемся формулой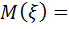 
:
16. Дискретная случайная величина 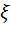имеет закон распределения
|
| |||
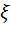
| р | 0,3 | 0,5 | 0,2 |
Найти дисперсию и среднее квадратическое отклонение случайной величины .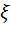
Решение. Дисперсию вычислим по формуле
Найдем для этого математическое ожидание квадрата случайной величины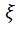 
:
Тогда
В соответствии с формулой 
находим среднее квадратическое отклонение 
17. Случайная величина 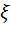задана плотностью вероятности:
Найти математическое ожидание и дисперсию случайной величины .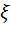
Решение. Найдем математическое ожидание и дисперсию случайной величины 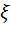по формулам:
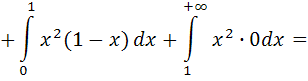
18. Случайная величина 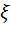распределена по нормальному закону, причем его параметры равны: т= 10, 
=2. Найти 
.
Решение. 
19. Для случайной величины 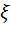известна дисперсия 
и неравенство 
Найти число а.
Решение. Согласно первому неравенству Чебышева
получаем 
Из этих неравенств следует, что
откуда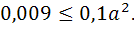 
Следовательно, 
20. Для случайной величины 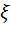известна дисперсия 
и
неравенство 
Найти значение 
.
Решение. Согласно второму неравенству Чебышева получаем
По условию 
. Из этих двух равенств следует, что 
