ЭМПИРИЧЕСКАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ

Пусть известно статистическое распределение частот количественного признака X. Введем обозначения:

· n_х - число наблюдений, при которых наблюдалось значение признака, меньше х;

· n - общее число наблюдений (объем выборки).

Ясно, что относительная частота события X < х равна n_х/n. Если х изменяется, то, вообще говоря, изменяется и относительная частота, т. е. относительная частота n_x/n есть функция от х. Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической.

Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(х), определяющую для каждого значения х относительную частоту события X < х.

Итак, по определению,

F^*(х) = n_х/n,

где n_х - число вариант, меньших х; n - объем выборки.

Таким образом, для того чтобы найти, например, F*(x₂), надо число вариант, меньших х₂, разделить на объем выборки:

В отличие от эмпирической функции распределения выборки функцию распределения F (х) генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция F(х) определяет вероятность события X<х, а эмпирическая функция F*(х) определяет относительную частоту этого же события. Из теоремы Бернулли следует, что относительная частота события X<х, т. е. F*(х) стремится по вероятности к вероятности F(х) этого события. Другими словами, при больших n числа F*(х) и F(х) мало отличаются одно от другого в том смысле, что

 

Уже отсюда следует целесообразность использования эмпирической функции распределения выборки для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности.

Такое заключение подтверждается и тем, что F*(х) обладает всеми свойствами F(х). Действительно, из определения функции F*(х) вытекают следующие ее свойства:

1) значения эмпирической функции принадлежат отрезку [0, 1];

2) F*(х) - неубывающая функция;

3) если х₁ - наименьшая варианта, то F*(x) = 0 при х£х₁, если x_k - наибольшая варианта, то F*(x)=1 при x>x_k.

Итак, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

Пример. Построить эмпирическую функцию по данному распределению выборки:

варианты xi
частоты ni

Решение

Найдем объём выборки: 12 + 18 + 30 = 60.

Наименьшая варианта равна 2, следовательно,

F*(x)=0 при х<2.

Значение X < 6, а именно х₁ = 2 и х₂ = 6, наблюдалось 12 раз, следовательно,

F*(х) = 12/60 = 0,2 при 2<х£6

Значения X < 10, а именно х₁ = 2 и х₂ = 6, наблюдались 12 + 18 = 30 раз, следовательно,

F*(х) = 30/60 = 0,5 при 6 < х£10.

Так как х=10 - наибольшая варианта, то

F*(х) = l при х>10.

Искомая эмпирическая функция

 

График этой функции изображен на рис. 1.

Рис.1.

 

ПОЛИГОН И ГИСТОГРАММА

Для наглядности строят различные графики статистического распределения и, в частности, полигон и гистограмму.

Полигоном частот называют ломаную, отрезки которой соединяют точки (х₁; n₁), (х₂; n₂),...., (x_k; n_k). Для построения полигона частот на оси абсцисс откладывают варианты х_i, а на оси ординат - соответствующие им частоты n_i. Точки (х_i; n_i) соединяют отрезками прямых и получают полигон частот.

Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (х₁; W₁), (х₂; W₂),... (x_k; W_k). Для построения полигона относительных частот на оси абсцисс откладывают варианты x_i, а на оси ординат - соответствующие им относительные частоты W_i. Точки (х_i; W_i) соединяют отрезками прямых и получают полигон относительных частот.

На рис. 2 изображен полигон относительных частот следующего распределения:

xi	1,5	3,5	5,5	7,5
Wi	0,1	0,2	0,4	0,3

 

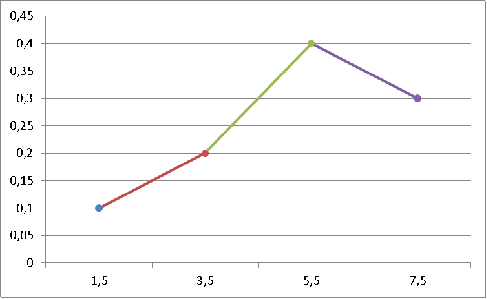
Рис.2.

В случае непрерывного признака целесообразно строить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала n_i - сумму частот вариант, попавших в i-й интервал.

Для выбора оптимальной величины интервала рекомендуется использовать формулу:

где x_max и x_min - соответственно наибольшее и наименьшее значение віборки, n - объем выборки.

Если задано интервальное статистическое распределение выборки, то для построения полигона частот или емпирических вероятностей по данным выборки соединяют точки, абсциссами которых являются середины частичных интервалов, а ординатами - соответствующие им значения частот или емпирических вероятностей.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению n_i/h (плотность частоты).

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии n_i/h.

Площадь i-го частичного прямоугольника равна hn_i/h = n_i -сумме частот вариант i-гo интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т. е. объему выборки.

На рис. 3 изображена гистограмма частот распределения объема n = 100, приведенного в табл. 1.

Таблица 1.

Частичный интервал	Сумма частот вариант ni	Плотность частоты ni/h
5-10		0,8
10-15		1,2
15-20		3,2
20-25		7,2
25-30		4,8
30-35		2,0
35-40		0,8

 

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению W_i/h (плотность относительной частоты).

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии W_i/h. Площадь i-го частичного прямоугольника равна hW_i/h = W_i - относительной частоте вариант, попавших в i-ый интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т. е. единице.

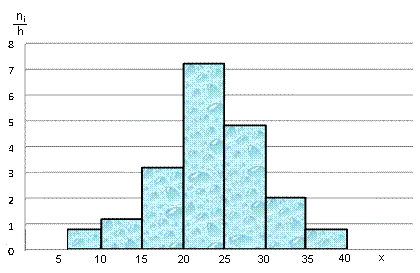
Рис.3.

Пример. Выборка задана распределением частот:

xi
ni

Построить гистограмму относительных частот.

Решение

Чтобы построить гистограмму относительных частот, нужно преобразовать на интервальное статистическое распределение относительных частот (эмпирических вероятностей) и найти плотность этих относительных частот. Для этого сначала определим объем выборки и эмпирические вероятности:

n=2+3+5+1+4+2+3=20,

Найдем длину частичных интервалов, частичные интервалы и плотность относительных частот. Частичные интервалы определим из условия, что заданные в дискретном статистическом распределении варианты должны быть серединами частичных интервалов.

Следовательно, длина частичных интевалов:

h = x_i+1 - x_i =2,

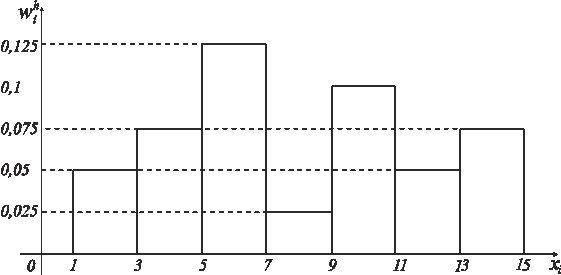
Искомое интервальное статистическое распределение эмпирических вероятностей имеет такой вид:

(хі; хi+1]	(1;3]	(3; 5]	(5; 7]	(7; 9]	(9; 11]	(11; 13]	(13; 15]
Wi	0,1	0,15	0,25	0,05	0,2	0,1	0,15

Плотности емпирических вероятностей такие:

Теперь можно легко построить искомую гистограмму относительных частот.

 

 

Пример 2. Исследователь, который определяет интенсивность труда рабочих механического цеха в отчетном году в процентах до прошлого года, получил таблицу частот:

Изделия, %	80-90	90-100	100-110	110-120
Количество рабочих я

Записать статистическое распределение.

 

Пусть случайная величина — интенсивность труда одного рабочего. Шаг таблицы частот h = 10, а ширина выборки — 40. Определим середины интервалов: х₁ = 85; х₂ = 95; х₃ = 105; х₄ = 115. Вычислим относительные частоты: (w₁ = 0,1; w₂ = 0,2; w₃ = 0,5; w₄= 0,2. Следовательно, статистическое распределение имеет вид:

х
w	0,1	0,2	0,5	0,2