Методы принятия управленческих решений
Методические указания для выполнения контрольной работы
для студентов заочной формы обучения
направления 080200.62 Менеджмент

Красноярск – 2013
Рецензент: д-р техн. наук, профессор А. Н. Антамошкин
Ступина А. А., Ежеманская С. Н.
Методы принятия управленческих решений. Методические указания для выполнения контрольной работы для студентов заочной формы обучения направления 080200.62 Менеджмент /А. А. Ступина, С. Н. Ежеманская. - Красноярск: НОУ ВПО СИБУП, 2013. – 64 с.
Предназначено для студентов направления 080200.62 Менеджмент заочной формы обучения. Учебно-методическое пособие охватывают основные темы курса дисциплины математика, раздел: экономико-математические методы. Пособие содержит краткий теоретический материал и 5 вариантов контрольной работы по дисциплине методы принятия управленческих решений.
Методические указания утверждены и одобрены к печати научно-методическим советом СИБУП от 2013 г. Протокол №
(c) Ежеманская С. Н., 2013
(c) Ступина А. А., 2013
(c) Сибирский институт бизнеса, управления и психологии, 2013
Содержание
Правила выполнения контрольной работы ………………….…..….. 4
Введение ………………………………………………………..……….. 5
1. Задачи линейного программирования………………………..….. 7
1.1 Основные определения и понятия …………………......... 7
1.2 Задания …………………………………..……………….. 18
2. Транспортная задача …………………………………..……..……… 24
2.1 Основные определения и понятия ……….…………….. 24
2.2 Задания ……………………………………………..….….. 29
3. Целочисленное программирование ……….………..…..………….. 30
4. Динамическое программирование ……………..………………..…. 33
4.1 Основные определения и понятия ………….................... 33
4.2 Задания …………………………………………………….. 36
5. Графы ………………………………………………………………... 38
5.1 Основные определения и понятия …………….……..….. 38
5.2 Задания …………………………………………………….. 41
6. Сетевое планирование ……………………………………………… 44
6.1 Основные определения и понятия …………………..….. 44
6.2 Задания …………………………………………………..….. 46
7. Системы массового обслуживания (СМО) ……………………….. 47
7.1 Основные определения и понятия …………………..….. 47
7.2 Задания …………….……………………….……………….. 51
8. Игры ……………………………………………………………….…. 52
8.1 Основные определения и понятия ………………………. 52
8.2 Задания …………………………………….….…………….. 54
Вопросы по курсу «Методы принятия управленческих решений»…...57
Библиографический список……………….…………………………...... 59
Приложение 1. Образец оформления титульного листа ……………….60
Правила выполнения контрольной работы
Номер варианта выберите согласно последней цифре номера зачётной книжки (смотри в таблице):
| Последняя цифра № зачётки | Номер варианта |
| 1 или 6 | |
| 2 или 7 | |
| 3 или 8 | |
| 4 или 9 | |
| 5 или 0 |
Работа оформляется в обыкновенной тетради в клетку.
При выполнении контрольной работы необходимо соблюдать следующие правила:
1. Оформить титульный лист по образцу (Приложение 1).
2. Решения задач располагать в порядке номеров, указанных в контрольных работах. В начале каждого решения записывать условие задачи (без сокращений).
3. Решения задач и объяснения к ним должны быть подробными, аккуратными, без сокращения слов. Обязательно, если требуется, выполнять чертежи с пояснениями.
Контрольные работы, выполненные с нарушением изложенных правил или не своего варианта, не засчитываются и возвращаются без проверки.
Получив прорецензированную работу, студент обязан исправить в ней отмеченные ошибки и недочёты. Зачтённые контрольные работы предъявляются преподавателю при защите перед зачётом или экзаменом.
Введение
Курс «Методы принятия управленческих решений» рассматривает специальные математические методы решения экономических задач. Исследование различных процессов, в том числе и экономических, обычно начинается с их моделирования, т.е. отражения реальных процессов через математические соотношения. При этом составляются уравнения или неравенства, которые связывают определенные показатели (переменные) исследуемого процесса, образуя систему ограничений. В этих соотношениях выделяют такие переменные, меняя которые можно получить оптимальное значение основного показателя данной системы (прибыль, доход, затраты и т. п.). Методы, позволяющие решать указанные задачи, объединяются под общим названием «исследование операций» (ИО).
Операция – любое мероприятие или система действий, объединённое единым замыслом и направленное на достижение определённой цели. Операция всегда является управляемым мероприятием, т.е. от нас зависит выбор некоторых параметров, характеризующих это мероприятие. Всякий выбор зависящих от нас параметров будем называть решением.
Решения могут быть удачными или неудачными. Оптимальным называется решение, которое по тем или иным соображениям предпочтительнее других.
Основная задача ИО – количественное обоснование оптимальных решений.
ИО включает в себя такие разделы математики, как математическое программирование, теорию игр, теорию массового обслуживания и др.
Математическое программирование – раздел высшей математики, посвященный решению задач, связанных с нахождением экстремумов функций (целевых функций) нескольких переменных при наличии ограничений на эти переменные.
В общем виде задача математического программирования имеет вид:
f(X) → min(max); X є D, (1)
где X = (x 1, x 2,..., x n) – вектор переменных задачи;
D – область допустимых значений переменных x 1, x 2,..., x n, задаваемая системой ограничений в виде уравнений и неравенств;
f(X) – целевая функция, характеризующая качество решения задачи.
В математическом программировании в зависимости от вида целевой функции f(X) и области D принято выделять следующие основные задачи:
- задачи линейного программирования, если f(X) и D линейны по X;
- задачи дискретного (целочисленного) программирования, если ставится условие целочисленности переменных x 1, x 2,..., x n;
- задачи нелинейного программирования, если f(X) и D нелинейны по X;
- задачи динамического программирования, если оптимизация целевой функции f(X) сводится к поэтапной оптимизации некоторых промежуточных целевых функций.
1. Задачи линейного программирования
1.1 Основные определения и понятия
Общая задача линейного программирования (ОЗЛП) формулируется следующим образом – найти переменные задачи x 1, x 2,..., x n, которые обеспечивают экстремум целевой функции
 (1.1)
(1.1)
Допустимым решением (планом) задачи линейного программирования (ЗЛП) называется любой n -мерный вектор X =(x 1, x 2,..., x n), удовлетворяющий системе ограничений равенств и неравенств. Множество допустимых решений задачи образует область допустимых решений D.
Оптимальным решением (планом) задачи линейного программирования называется такое допустимое решение, при котором целевая функция Z (X) достигает экстремума.
Каноническая задача линейного программирования (КЗЛП) имеет вид
 (1.2)
(1.2)
Она отличается от ОЗЛП тем, что её система ограничений является системой только уравнений и все переменные неотрицательные.
Приведение ОЗЛП к каноническому виду ЗЛП:
- чтобы заменить исходную задачу минимизации на задачу максимизации (или наоборот задачу максимизации на задачу минимизации) достаточно целевую функцию умножить на «-1» и искать максимум (минимум) полученной функции;
- если среди ограничений имеются неравенства, то путем введения дополнительных неотрицательных переменных x n+1 ≥ 0 они преобразуются в равенства:
неравенство a i1 x 1+…+ a in x n ≥ b i заменяется на равенство a i1 x 1+…+ a in x n + x n+1 = b i,
неравенство a i1 x 1+…+ a in x n ≤ b i заменяется на равенство a i1 x 1+…+ a in x n + x n+1 = b i;
- если некоторая переменная xk не имеет ограничений по знаку, то она заменяется (в целевой функции и во всех ограничениях) разностью между двумя новыми неотрицательны-ми переменными: xk = x'k – x”k, где x'k ≥ 0. x”k ≥ 0.
Графический метод решения ЗЛП с двумя неизвестными
ЗЛП с двумя неизвестными имеет вид:

Метод основан на возможности графического изображения области допустимых решений и нахождении среди них оптимального решения.
Область допустимых решений (ОДР) задачи является выпуклым многоугольником и строится как пересечение (общая часть) областей решений каждого из неравенств ограничений задачи.
Областью решения неравенства a i1 x 1+ a i2 x 2 ≤ b i является одна из двух полуплоскостей, на которые прямая a i1 x 1+ a i2 x 2 = b i, соответствующая этому неравенству, делит координатную плоскость. Чтобы определить, какая из двух полуплоскостей является областью решений, достаточно координаты какой-либо точки, не лежащей на разделяющей прямой подставить в неравенство:
- если неравенство справедливо, то областью решений является полуплоскость, содержащая эту точку;
- если неравенство не справедливо, то областью решений является полуплоскость, не содержащая эту точку.
Для нахождения среди допустимых решений оптимального используются линии уровня.
Линией уровня называется прямая с 1 x 1+ с 2 x 2 = l, где l= const, на которой целевая функция задачи принимает постоянное значение. Все линии уровня параллельны между собой.
Градиент целевой функции grad Z (X) задает вектор нормали
C = (c 1, c 2) линий уровня. Целевая функция на линиях уровня возрастает, если линии уровня перемещать в направлении их нормали, и убывает – в противоположном направлении.
Опорной прямой называется линия уровня, которая имеет хотя бы одну общую точку с ОДР и по отношению к которой ОДР находится в одной из полуплоскостей. ОДР задачи имеет не более двух опорных прямых.
Оптимальное решение ЗЛП лежит на опорной прямой в угловой точке многоугольника ОДР. ЗЛП имеет единственное решение, если опорная прямая проходит через одну угловую точку ОДР, бесконечное множество решений, если опорная прямая проходит через ребро многоугольника ОДР. ЗЛП не имеет решения, если ОДР является пустым множеством (когда система ограничений несовместна) и если ОДР неограниченна в направлении экстремума (целевая функция неограниченна).
Алгоритм графического метода решения ЗЛП с двумя неизвестными:
1. Построить ОДР.
2. Построить вектор нормали C = (c 1, c 2) и линию уровня с 1 x 1+ с 2 x 2 = 0, проходящую через начало координат и перпендикулярную вектору С.
3. Передвигать линию уровня до опорной прямой в направлении вектора С в задаче на max, или в противоположном направлении – в задаче на min.
4. Если при перемещении линии уровня в направлении экстремума ОДР уходит в бесконечность, то ЗЛП не имеет решения ввиду неограниченности целевой функции.
5. Если ЗЛП имеет оптимальное решение, то для его нахождения решить совместно уравнения прямых, ограничивающих ОДР и имеющих общие точки с опорной прямой. Если экстремум достигается в двух угловых точках, то ЗЛП имеет бесконечное множество решений, принадлежащих ребру ОДР, ограниченному этими угловыми точками. В данном случае вычисляются координаты обеих угловых точек.
6. Вычислить значение целевой функции в точке экстремума.
Симплекс-метод решения ЗЛП
Симплекс-метод основывается на следующих положениях:
- ОДР задачи линейного программирования является выпуклым множеством с конечным числом угловых точек;
- Оптимальным решением ЗЛП является одна из угловых точек ОДР. Угловые точки ОДР алгебраически представляют некоторые базисные (опорные) решения системы ограничений ЗЛП.
Базисным (опорным) решением ЗЛП называется такое допустимое решение X 0 =(x 10, x 20,..., x m0, 0,…0), для которого векторы условий (столбцы коэффициентов при неизвестных в системе ограничений) линейно независимы.
Ненулевые координаты x 10, x 20,..., x m0 решения X 0 называются базисными переменными, оставшиеся координаты решения X 0 - свободными переменными. Число отличных от нуля координат опорного решения не может быть больше ранга r системы ограничений ЗЛП (числа линейно независимых уравнений в системе ограничений ЗЛП). Далее считаем, что система ограничений ЗЛП состоит из линейно независимых уравнений, т.е. r = m.
Смысл симплекс-метода заключается в целенаправленном переходе от одного опорного решения ЗЛП к другому (т.е. от одной угловой точки ОДР к другой) в направлении экстремума и состоит в последовательности этапов:
- найти начальное опорное решение;
- осуществить переход от одного опорного решения к другому;
- определить критерий достижения оптимального решения или сделать заключение об отсутствии решения.
Алгоритм выполнения Симплекс-метода ЗЛП
Алгоритм симплекс-метода осуществляет переход от одного опорного решения ЗЛП к другому в направлении экстремума целевой функции.
Пусть ЗЛП задана в каноническом виде (1.2) и выполнено условие
b i ≥ 0, i =1,2,…, m, (1.3)
соотношение (1.3) всегда можно выполнить, домножив соответствующее уравнение на «-1» в случае отрицательности b i. Также считаем, что система уравнений в ограничениях задачи (1.2) линейно независима и имеет ранг r = m. При этом вектор опорного решения имеет m ненулевых координат.
Пусть исходная задача (1.2), (1.3) приведена к виду, где базисные переменные x 1, x 2,..., x m выражены через свободные переменные xm+ 1, x m+ 2,..., x n
 (1.4)
(1.4)
На основе этих соотношений построим таблицу 1
Таблица 1.

Таблица 1 называется симплекс-таблицей. Все дальнейшие преобразования связаны с изменениями содержания этой таблицы.
Алгоритм симплекс-метода:
1. В последней строке Z симплекс-таблицы в задаче на min находят наименьший положительный элемент (в задаче на max - наименьший отрицательный элемент), не считая свободного члена. Столбец, ответствующий этому элементу, называется разрешающим.
2. Вычисляют отношение свободных членов к положительным элементам разрешающего столбца (симплекс-отношение). Находят наименьшее из этих симплекс - отношений, оно соответствует разрешающей строке.
3. На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент.
4. Если имеется несколько одинаковых по величине симплекс - отношений, то выбирают любое из них. То же самое относится к положительным элементам последней строки симлекс - таблицы.
5. После нахождения разрешающего элемента переходят к следующей таблице. Неизвестные переменные, соответствующие разрешающей строке и столбцу, меняют местами. При этом базисная переменная становится свободной переменной и наоборот. Симплекс - таблица преобразуется следующим образом (таблица 2):
Таблица 2
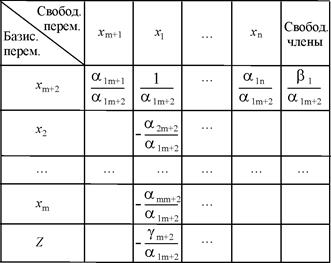
6. Элемент таблицы 2, соответствующий разрешающему элементу таблицы 1, равен обратной величине разрешающего элемента.
7. Элементы строки таблицы 2, соответствующие элементам разрешающей строки таблицы 1, получаются путем деления соответствующих элементов таблицы 1 на разрешающий элемент.
8. Элементы столбца таблицы 2, соответствующие элементам разрешающего столбца таблицы 1, получаются путем деления соответствующих элементов таблицы 1 на разрешающий элемент и берутся с противоположным знаком.
9. Остальные элементы вычисляются по правилу прямоугольника: мысленно вычерчиваем прямоугольник в таблице 1, одна вершина которого совпадает с разрешающим элементом (Рэ), а другая – с элементом, который мы ищем; обозначим элемент в новой таблице 2 через (Нэ), а элемент, стоящий на этом же месте в старой таблице 1 – через (Сэ). Остальные две вершины А и В дополняют фигуру до прямоугольника. Тогда искомый элемент Нэ из таблицы 2 равен Нэ = Сэ – А*В/Рэ.
10. Критерий оптимальности. Как только получится таблица, у которой в последней строке в задаче на min все элементы отрицательны (в задаче на max все элементы положительны), считается, что экстремум найден. Оптимальное значение целевой функции равно свободному члену в строке Z, а оптимальное решение определяется свободными членами при базисных переменных. Все свободные переменные полагаются равными нулю.
11.Если в разрешающем столбце все элементы отрицательны, то задача не имеет решений (минимум не достигается).
Метод искусственного базиса решения ЗЛП
Алгоритм симплекс-метода применим, если выделено какое-либо опорное решение ЗЛП, т. е, исходная ЗЛП (1.2) приведена к виду (1.4). Метод искусственного базиса предлагает процедуру построения такого опорного решения.
Метод искусственного базисаоснован на введении искусственных базисных переменных y 1, y 2,…, y m, с помощью которых система ограничений ЗЛП (2.2)
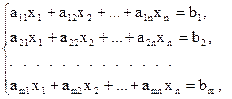 (1.5)
(1.5)
может быть преобразована к виду
 (1.6)
(1.6)
Системы (1.5) и (1.6) будут эквивалентны в том случае, если все yi будут равны нулю. Как и раньше мы считаем, что все bi ≥ 0. Для того чтобы уi были равны 0, мы должны преобразовать задачу таким образом, чтобы все искусственные базисные переменные yi перешли в свободные переменные. Такой переход можно сделать алгоритмом симплекс метода относительно дополнительной целевой функции
F (y) = y 1+ y 2 +... + y m = d 0 – (d 1 x 1+ d 2 x 2+…+ d n x n). (2.7)
Исходная симплекс таблица для данного метода имеет вид

Сначала симплекс таблица преобразуется относительно целевой функции F (y) до получения опорного решения. Опорное решение найдено, когда выполнен следующий критерий: F (y) = 0 и все искусственные переменные уi переведены в свободные переменные. Затем из симплекс таблицы вычеркивается строка для F (y) и столбцы для уi и решают задачу для исходной целевой функции Z (x) до получения оптимального решения.
Рекомендуется вводить минимум искусственных переменных.
Двойственные задачи линейного программирования
Пара задач линейного программирования называется симметричной двойственной парой, если они удовлетворяют условиям:
1. число неизвестных одной задачи равно числу ограничений другой задачи;
2. матрица коэффициентов системы ограничений получается одна из другой путем транспонирования;
3. неравенства в системах ограничений имеют противоположный смысл;
4. свободные члены системы ограничений одной из задач становятся коэффициентами целевой функции другой задачи, коэффициенты целевой функции превращаются в свободные члены ограничений;
5. целевые функции в задачах имеют противоположный смысл: в первой – max, во второй – min.
Одна из таких задач называется прямой (основной), а другая – двойственной
Прямая Двойственная

• Одна
условие целочисленности переменных x 1, x 2,..., x n;
- задачи нелинейного программирования, если f(X) и D нелинейны по X;
- задачи динамического программирования, если оптимизация целевой функции f(X) сводится к поэтапной оптимизации некоторых промежуточных